This is an old version of my web page, in a few seconds you will be automatically redirected to my new site.
Tracking an Omnidirectional Evader with a Differential Drive Robot
 |
We consider the surveillance problem of tracking a moving evader by a nonholonomic mobile
pursuer. We deal specifically with the situation in which the only constraint on the evader's velocity is a bound on speed
(i.e., the evader is able to move omnidirectionally), and the pursuer is a nonholonomic, differential drive system having bounded speed.
We formulate our problem as a game. Given the evader's maximum speed, we determine a lower bound for the required
pursuer speed to track the evader. This bound allows us to determine at the beginning of the game whether or not
the pursuer can follow the evader based on the initial system configuration. We then develop the system model, and
obtain optimal motion strategies for both players, which allow us to establish the long term solution for the game. We
present an implementation of the system model, and motion strategies, and also present simulation results of the pursuit-evasion game. [Video1] [Video2] |
|
Tracking an Omnidirectional Evader with a Differential Drive Robot |
A Homicidal Differential Drive Robot
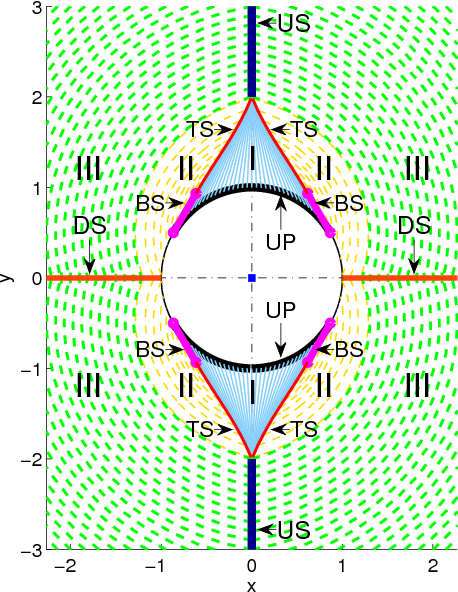 |
We consider the problem of capturing an omnidirectional evader using a Differential Drive Robot
in an obstacle free environment. At the beginning of the game the evader is at a distance L > l from the pursuer. The pursuer
goal is to get closer from the evader than the capture distance l. The goal of the evader is to keep the pursuer at all time
farther from it than this capture distance. In this work, we found closed-form representations of the motion primitives and
time-optimal strategies for each player. These strategies are in Nash Equilibrium, meaning that any unilateral deviation
of each player from these strategies does not provide to such player benefit toward the goal of winning the game. We also
present the condition defining the winner of the game and we construct a solution over the entire reduced space. |
|
A Homicidal Differential Drive Robot |