Componentes Principales
1."Smoothing" de los datos.
Para evitar errores grandes en los primeros y últimos meses, debidos a la ciclicidad,
simplemente pegamos una copia de los datos antes y una copia después. Finalmente seleccionamos
"la copia de enmedio"
Para seleccionar el nivel de suavizado, utilizamos los "sliders" de tcl,
una vez ajustado el nivel de suavizado lo aplicamos a todos los datos.
El código en R es:
######cargamos los datos y agregamos los nombres de filas y columnas########
datosSinUbicacion<-read.table('monthtemp.dat');
etiquetas<-c("St. John_s", "Charlottetown", "Halifax" ,
"Sydney", "Yarmouth", "Fredericton",
"Arvida", "Montreal", "Quebec City",
"Schefferville", "Sherbrooke", "Kapuskasing",
"London", "Ottawa", "Thunder Bay",
"Toronto", "Churchill", "The Pas",
"Winnipeg", "Prince Albert", "Regina",
"Beaverlodge", "Calgary", "Edmonton",
"Kamloops", "Prince George", "Prince Rupert",
"Vancouver", "Victoria", "Dawson",
"Whitehorse", "Frobisher Bay", "Inuvik",
"Resolute", "Yellowknife");
colnames(datosSinUbicacion)<-c("Ene", "Feb","Mar","Abr","May","Jun","Jul","Ago","Sep","Oct","Nov","Dic");
rownames(datosSinUbicacion)<-etiquetas;
library(tcltk);
##simplemente muestra cómo quedarían los datos para un valor dado de Bandwidth##
suavizarRenglon<-function(...)
{
copia<-rep(datosSinUbicacion[as.numeric(tclvalue(numEstacion)),], 3);
suavizado<-ksmooth(x=1:36,
y=copia,
"normal",
bandwidth=as.numeric(tclvalue(rigidez)),
n.points=36, x.points=1:36);
plot(x=13:24, y=copia[13:24]);
lines(suavizado$x[13:24], suavizado$y[13:24]);
}
##Esta función aplica el suavizado seleccionado##
aplicarSuavizado<-function(...)
{
numRenglones<-length(datosSinUbicacion[,1]);
for(i in 1:numRenglones)
{
copia<-rep(datosSinUbicacion[i,], 3);
suavizado<-ksmooth(x=1:36,
y=copia,
"normal",
bandwidth=as.numeric(tclvalue(rigidez)),
n.points=36,
x.points=1:36
);
datosSinUbicacion[i,]<<-suavizado$y[13:24];
}
}
##Inicializamos la ventana principal de tcl##
numEstaciones<-length(datosSinUbicacion[,1]);
ventanaPrincipal<-tktoplevel();
numEstacion<-tclVar(1);##Esta variable indica el número de estación a visualizar##
rigidez<-tclVar(0.5); ##Esta variable indica el valor de Bandwidth##
selectorEstacion<-tkscale(ventanaPrincipal, ##Slider para el número de estación##
from=1,
to=numEstaciones,
showvalue=T,
variable=numEstacion,
resolution=1,
command=suavizarRenglon);
selectorRigidez<-tkscale(ventanaPrincipal, ##Slider para el valor de Bandwidth##
from=0.5,
to=10,
showvalue=T,
variable=rigidez,
resolution=0.01,
command=suavizarRenglon);
botonAplicarSuavizado<- tkbutton(ventanaPrincipal, ##Botón para aplicar el suavizado##
text="Ya!!",
command=aplicarSuavizado);
tkgrid(selectorEstacion, selectorRigidez, botonAplicarSuavizado);
tkfocus(ventanaPrincipal);
2) Análisis de componentes principales.
Nota: Los resultados son diferentes si usamos la correlación que si usamos la matriz de covarianzas.
Dado que las mediciones son del mismo tipo (rangos y resolución similares) NO deberíamos usar la
correlación, pero como esta es una tarea "de exploración" pues hice los experimentos:
Sin usar la correlación
Código en R para visualizar las dos primeras componentes (como curva):
##Calculamos las componentes principales y visualizamos la primera contra la segunda##
pcaSin<-princomp(datosSinUbicacion); ##En este caso NO es conveniente utilizar la matriz de correlación##
biplot(pcaSin);
##Ahora para visualizar las dos primeras componentes principales (como curva)##
par(mfrow=c(1, 2))
plot(pcaSin$loadings[,1]);
lines(1:12, pcaSin$loadings[,1]);
plot(pcaSin$loadings[,2]);
lines(1:12, pcaSin$loadings[,2]);
Interpretación
- En el primer componente, todos los coeficientes son negativos, por lo que se trata de un promedio de las temperaturas a lo largo del año
dando una ligera importancia a las temperaturas correspondientes a meses frios sobre meses cálidos
(los coeficientes en valor absoluto son mayores).
- El segundo componente también es bastante claro, tenemos coeficientes positivos en los extremos de
la curva y negativos en el centro. Si consideramos que las temperaturas son típicamente "bajo cero"
en invierno (extremos de la curva) y consideramos también la ciclicidad, lo que tenemos es un contraste
entre las temperaturas de meses frios y temperaturas de meses cálidos.
Usando la matriz de correlación
Código en R para visualizar las dos primeras componentes (como curva):
##Calculamos las componentes principales y visualizamos la primera contra la segunda##
pcaSin<-princomp(datosSinUbicacion, cor=TRUE);
biplot(pcaSin);
##Ahora para visualizar las dos primeras componentes principales (como curva)##
par(mfrow=c(1, 2))
plot(pcaSin$loadings[,1]);
lines(1:12, pcaSin$loadings[,1]);
plot(pcaSin$loadings[,2]);
lines(1:12, pcaSin$loadings[,2]);
Los rasgos son evidentes!!:
- En la curva del primer componente es fácil distinguir "dos picos"
(si consideramos la ciclicidad, claro!), el primero en los meses extremos (Enero, Diciembre),
y otro en los meses centrales (Junio, Julio). Significa que La información está concentrada
en los niveles de temperatura en invierno y verano. Los coeficientes son todos negativos, por lo que se
trata de un "promedio" de temperaturas considerando especialmente las temperaturas de invierno y verano.
- El segundo componente también es bastante claro, tenemos coeficientes negativos en los extremos de
la curva y positivos en el centro. Si consideramos que las temperaturas son típicamente "bajo cero"
en invierno (extremos de la curva) y consideramos también la ciclicidad, lo que tenemos es una
especie de "kernel gausiano de derivación", es decir, se trata de un contraste
Uno se puede "ir con la finta" si no considera ciclicidad, es mejor ver los componentes trasladados, a la
izquierda están los meses correspondientes al verano y a la derecha al invierno:
Aquí se aprecian mas claramente los dos picos en el primer componente y el contraste del segundo componente.
Con esto en mente, ahora si conviene ver la grafica del primer componente contra el segundo.
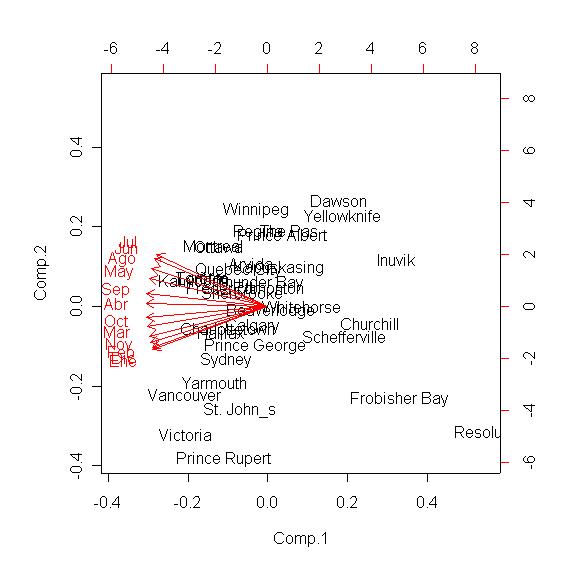
De izquierda a la derecha vemos las estaciones de lugares cálidos a fríos (el cambio de sentido se debe al
signo de los coeficientes del primer componente).
En la vertical, del centro hacia afuera (arriba-abajo)tenemos las estaciones de temperaturas "muy constantes" a temperaturas "muy variables".
Agrupar las estaciones es una tarea muy subjetiva, yo agrupé las regiones "cercanas" en la gráfica del
primer componente contra el segundo. Agrego el codigo para seleccionar manualmente los puntos y luego verlos espacialmente
(antes hay que correr el codigo para cargar los datos y obtener los componentes principales):
eigenVectors<-data.matrix(pcaSin$loadings[,1:12]);
X<-data.matrix(datosSinUbicacion);
numObs<-length(datosSinUbicacion[,1]);
comp1<-rep(0,numObs);
comp2<-rep(0,numObs);
for(i in 1:numObs)
{
comp1[i]<-(((X[i,]-pcaSin$center)/pcaSin$scale)%*%eigenVectors[,1]);
comp2[i]<-(((X[i,]-pcaSin$center)/pcaSin$scale)%*%eigenVectors[,2]);
}
plot(comp1, comp2);
seleccionados<-identify(comp1, comp2, labels=etiquetas);
colores<-rep("black", numObs);
colores[seleccionados]<-"red";
plot(datosConUbicacion$Longitud, datosConUbicacion$Latitud, col=colores);
Algunos de los puntos conservan la cercanía espacial pero muchos otros no:
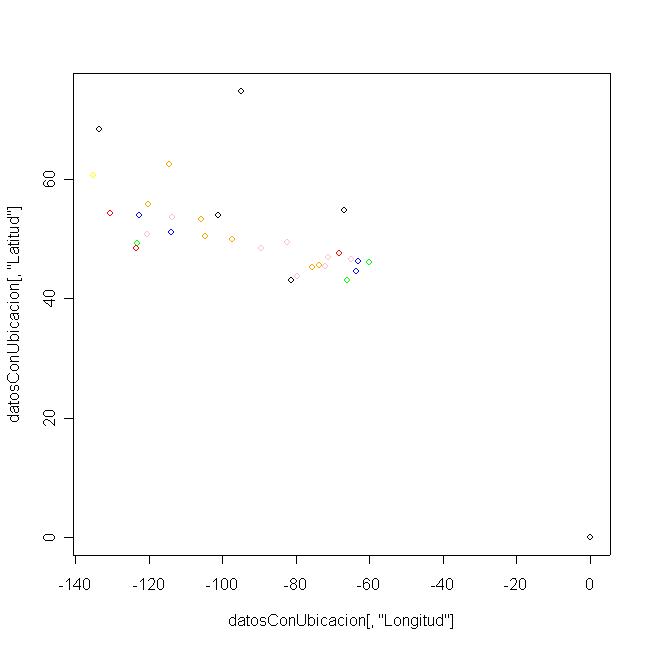
Los grupos que consideré son:
grupo1<-c("Prince Rupert","Victoria","St. John_s");
grupo2<-c("Vancouver","Yarmouth","Sydney");
grupo3<-c("Prince George","Halifax","Charlottetown", "Calgary");
grupo4<-c("Whitehorse","Beaverlodge");
grupo5<-c("Quebec City","Arvida","Kapuskasing", "Thunder Bay", "Kamloops", "Toronto", "Sherbrooke", "Fredericton", "Edmonton");
grupo6<-c("Montreal", "Ottawa", "Regina", "Prince Albert", "Winnipeg", "Dawson", "Yellowknife");
y los colores:
colores<-as.matrix(rep("black",numObs));
rownames(colores)<-etiquetas;
colores[grupo1,1]<-"red";
colores[grupo2,1]<-"green";
colores[grupo3,1]<-"blue";
colores[grupo4,1]<-"yellow";
colores[grupo5,1]<-"pink";
colores[grupo6,1]<-"orange";
los puntos negros son los que están muy dispersos en el biplot de componentes principales.
Para hacer el análisis considerando el dominio espacial, obtuve la ubicación de las estaciones (Longitud, Latitud)
y esos son los puntos que se ven en la gráfica anterior. El problema con esto es que no se aprecia las distancias
verdaderas debido al problema de ver la superficie del globo proyectada en un plano...
PCA usando la ubicación de las estaciones
También creí interesante hacer el análisis de componentes principales incluyendo
las coordenadas de las estaciones. Esta vez es necesario usar la matriz de correlación.
El archivo con los datos completos está en esta liga. La primera columna es la Latitud y
el segundo la Longitud (Norte, Este)
datosConUbicacion<-read.table('monthtempLoc.dat');
etiquetas<-c("St. John_s", "Charlottetown", "Halifax" ,
"Sydney", "Yarmouth", "Fredericton",
"Arvida", "Montreal", "Quebec City",
"Schefferville", "Sherbrooke", "Kapuskasing",
"London", "Ottawa", "Thunder Bay",
"Toronto", "Churchill", "The Pas",
"Winnipeg", "Prince Albert", "Regina",
"Beaverlodge", "Calgary", "Edmonton",
"Kamloops", "Prince George", "Prince Rupert",
"Vancouver", "Victoria", "Dawson",
"Whitehorse", "Frobisher Bay", "Inuvik",
"Resolute", "Yellowknife");
colnames(datosConUbicacion)<-c("Latitud","Longitud","Ene", "Feb","Mar","Abr","May","Jun","Jul","Ago","Sep","Oct","Nov","Dic");
rownames(datosConUbicacion)<-etiquetas;
datosConUbicacion<-datosConUbicacion[datosConUbicacion$Latitud!=0,];##No encontré la ubicación de 4 estaciones... hay que quitarlas
pcaCon<-princomp(datosConUbicacion, cor=TRUE);##En este caso sín necesitamos usar la correlación
biplot(pcaCon);
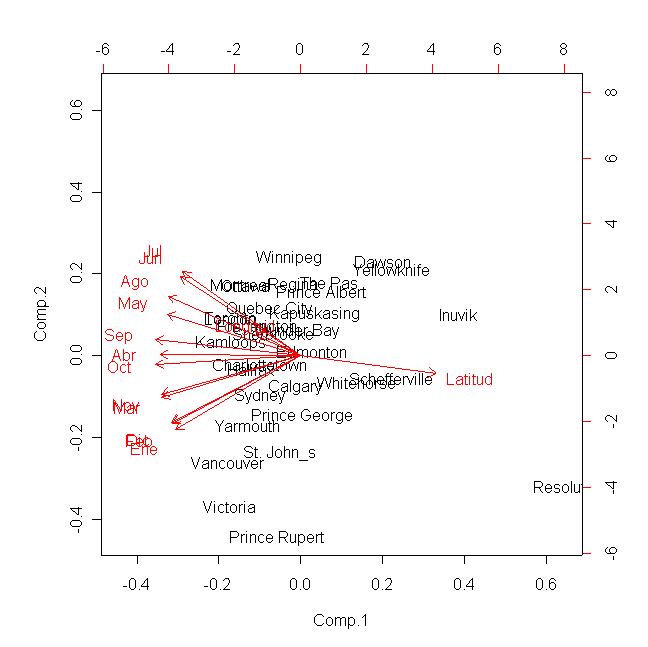
Ya no incluyo las gráficas de los componentes pero tienen prácticamente la misma forma solo que se le
da mucho mayor peso a la Latitud en el primer componente (eso se puede ver en la gráfica anterior).
Segundo ejercicio
Para hacer el segundo ejercicio, seguí el procedimiento indicado pero para valores pequeños de epsilon
no se observan cambios, es necesario tomar valores muy grandes...
los cambios...
epsilon<-1000;
X<-data.matrix(datosSinUbicacion);
Xmas<-X+epsilon*pcaSin$loadings[,3];
Xmenos<-X-epsilon*pcaSin$loadings[,3];
promedioPorMes<-colMeans(X);
promedioMas<-colMeans(Xmas);
promedioMenos<-colMeans(Xmenos);
par(mfrow=c(3, 1));
plot(promedioPorMes);
plot(promedioMas);
plot(promedioMenos);