Introducción a Python, Segunda Parte

Mariano Rivera

Agosto 2017

Revisaremos

Control de flujo
Funciones
Incluir librerias

Control de Flujo

For

Es necesario iterar sobre los elementos de objetos que acepten iteradores: Contenedores (Listas, por ejemplo)

*Notación tipo $\forall x \in X:$

*El comando del ciclo termina con dos puntos (:)

*El cuerpo de ciclo esta indentado, de hecho el editor lo hizo automáticamente.

*No hay un end para delimitar el ciclo, se delimita por el fin de la identación.

*Dado que la identación hace legibles los programas, en Python no de dejó opcional, es forzada (parte del diseño del lenguaje)

alumnos = ['Juan', 'Pedro','Elsa','Ana', 'Alberto','Judith',
           'Miguel', 'Oscar','Laura', 'Jose', 'Roberto', 
           'Andres', 'Maria']

for alumno in alumnos:
    print ('{} es alumno de mi clase'.format(alumno))
    
print ('Fin de lista')

Juan es alumno de mi clase
Pedro es alumno de mi clase
Elsa es alumno de mi clase
Ana es alumno de mi clase
Alberto es alumno de mi clase
Judith es alumno de mi clase
Miguel es alumno de mi clase
Oscar es alumno de mi clase
Laura es alumno de mi clase
Jose es alumno de mi clase
Roberto es alumno de mi clase
Andres es alumno de mi clase
Maria es alumno de mi clase
Fin de lista

funciones de los objetos Sets

mascotas = {'perro', 'gato', 'pajaro', 'tortuga', 'pez', 
            'conejo','lagartija'}
for idx, animal in enumerate(mascotas):
    print ('#{}:{}'.format(idx+1, animal))
    
print()
for idx, animal in enumerate(mascotas):
    print ('#{0}:{1}'.format(idx+1, animal))

#1:pez
#2:pajaro
#3:tortuga
#4:conejo
#5:gato
#6:perro
#7:lagartija

#1:pez
#2:pajaro
#3:tortuga
#4:conejo
#5:gato
#6:perro
#7:lagartija

While

Se usa para repetición en tanto una expression sea evaluada lógicamente como True

value =10
while value :    # puede interpretarse como while if value = True :
    print(value)
    value -=1

value =10
while value :
    print(value)
    value -=1
else:                # se evalua si la clausula en while falla
    print('termina el ciclo')

10
9
8
7
6
5
4
3
2
1
termina el ciclo

value =10
while value :
    print(value)
    value -=1
    break;    # evita la clausula else
else:
    print('termina el ciclo')

If y If-Else

Ejecución condicional o Bifurcaciones
Ya en while vimos in poco del un if-else.

value = True
if value:            # se ejecuta si le expresion es evaluada True
    print('value')
        
print('...')

value
...

value = False
if value:
    print('expresión cierta')
else:               # se ejecuta si le expresion es evaluada False
    print('expresion falsa')
        
print('...')

expresion falsa
...

Funciones

Una función es una estatuto ejecutable
La definición de la función no ejecuta su cuerpo, solo se ejecuta cuando se le invoca
El ámbito o alcance (scope) de las variables definidas dentro de una función es la misma función: las variabes son locales.
El cuerpo de una fucnión puede contener definición de otras funciones cuyo alcance se limita a dicha función.
Los parámetros se pasan a una función por referencia.

¿Se puede modificar el valor de una variable pasada a una función en Python? NO. Y no es deseable y no se necesita.

def g(a,b):
    a,b = b,a    # swap de los valores al interior

   
def f(a,b):
    a,b = b,a   
    return a,b  # regresa los valores intercambiados
    
a,b = 1,2
print ('original:', a,b)
g(a,b)
print ('        g: ', a,b)
a,b= f(a,b)
print ('        f: ', a,b)

original: 1 2
        g:  1 2
        f:  2 1

Parámetos por Default

Python acepta que se dé un valor a los parámetros el cual se usará en caso de que se omita ser pasado por el usuario.

El order de los parámetros por omisión será de izquierda a derecha.

Una buena técnica de programación defensiva es indicar el parámetro y su valor al momento de ser llamado.

Los parámetros que se indican con nombre no importa el orden en que se pasen.

def factorial(n=0):  
    if n<=0:
        return 1
    else:
        return n*factorial(n-1)   # Python permite recusión
y =factorial(100)
print(y)

93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

type(y)

int

x = factorial(1000)
type(x)

int

Llamada sin parámetro, se usa el valor por default

print(factorial())

Importancia de pasar Arreglos por Referencia

Solo los arreglos se pueden modificar al interior de una fucnión, no asi los escalares. Vea la diferencia entre n y x.

def f(n, x):
    n = 2
    x.append(4)
    print('In f():', n, x)

n = 1
x = [0,1,2,3]
print('Before:', n, x)
f(n, x)
print('After: ', n, x)

Before: 1 [0, 1, 2, 3]
In f(): 2 [0, 1, 2, 3, 4]
After:  1 [0, 1, 2, 3, 4]

Pasando COPIAS de los arreglos

Para evitar efectos no deseados sobre arreglos que pasamos, se pueden pasar copias. Pero implica doble uso de memoria.

n = 1
x = [0,1,2,3]
print('Before:', n, x)
f(n, x.copy())
print('After: ', n, x, ' <---!!!')

Before: 1 [0, 1, 2, 3]
In f(): 2 [0, 1, 2, 3, 4]
After:  1 [0, 1, 2, 3]  <---!!!

Pasando arreglos constantes = Tuplas (tuple)

Para evitar cambios no deseados dentro de funciones a arreglos que se pasan como parámetros, pasemos tuplas.

n = 1
x = [0,1,2,3]
print('Before:', n, x)
f(n, tuple(x))   # note el cambio de tipo, 'cast'
print('After: ', n, x)

Before: 1 [0, 1, 2, 3]



---------------------------------------------------------------------------

AttributeError                            Traceback (most recent call last)

<ipython-input-32-e321b6148e1f> in <module>()
      2 x = [0,1,2,3]
      3 print('Before:', n, x)
----> 4 f(n, tuple(x))   # note el cambio de tipo, 'cast'
      5 print('After: ', n, x)


<ipython-input-30-6f9bb4f12588> in f(n, x)
      1 def f(n, x):
      2     n = 2
----> 3     x.append(4)
      4     print('In f():', n, x)
      5 


AttributeError: 'tuple' object has no attribute 'append'

EJEMPLO. Generador de Números aleatorios (de Wikipedia)

Los algoritmos para la generación de valores uniformemente distribuidos están presentes en todas las calculadoras y lenguajes de programación, y suelen estar basados en congruencias numéricas del tipo:

$x_{n+1} \leftarrow (ax_{n}+c) \mod{m}$

El éxito de este tipo de generadores de valores de una variable aleatoria depende de la elección de los cuatro parámetros que intervienen inicialmente en la expresión anterior:

El valor inicial o semilla: $x_{0}$

La constante multiplicativa: $a$

La constante aditiva: $c$

El número $m$ respecto al cual se calculan los restos

Estos cuatro valores deben ser números enteros no negativos y que cumplan la siguiente condición:

$x_0, a, c <m$ .

#----------------------------------------------------------------------------
def aleatorios(n=100, seed= 56125798, c=12345, m=32768, a=1103515245):
    '''
    Genera n números aleatorios usando seed como valor inicial 
    con el algoritmo congruencias numéricas con constantes POSIX
    '''
    x=[]
    val = seed
    for i in range(n):
        val = (a*val+c)%m
        x.append(val)
        
    return x
#--------------------------------------------------------------------

x = aleatorios()
print(x)

[9383, 11604, 5373, 13810, 25667, 19136, 1017, 16190, 415, 21228, 26293, 4426, 6331, 12760, 14641, 30742, 1431, 4996, 14189, 32674, 25651, 25584, 23913, 29678, 4239, 20252, 26405, 24826, 9899, 16648, 20641, 4806, 647, 26036, 21981, 5458, 16419, 10528, 29401, 13470, 15231, 14156, 25493, 31914, 4251, 31800, 9233, 14710, 7031, 9188, 28749, 30466, 30739, 6736, 17481, 334, 623, 2940, 23557, 25690, 22155, 25448, 13185, 27686, 20583, 19988, 1725, 9394, 3075, 14208, 20921, 23038, 25951, 19372, 20597, 6154, 30843, 30360, 32497, 10966, 8535, 25668, 6445, 7778, 31731, 176, 6953, 16046, 25679, 30684, 16613, 6074, 30315, 13768, 1633, 30086, 3655, 26228, 10141, 25618]

Los parámetros por default se aplican de Izquierda a Derecha

print(aleatorios(5))     # es equivalente a print(aleatorios(n=5, ...))

[9383, 11604, 5373, 13810, 25667]

Es posible pasar solo algunos parámetros si los predecesores tienen valores por default, en tal caso debe especificarse cual:

# es equivalente a print(aleatorios(n=10, seed=83984, ...)) 
seed=78669
print(aleatorios(seed=seed))

[32258, 29459, 31056, 14153, 30798, 11631, 23164, 32517, 19290, 12683, 8808, 1665, 17190, 23399, 32020, 2493, 27570, 18179, 22144, 1209, 4350, 20575, 23212, 13173, 16138, 4987, 30104, 4593, 16854, 27735, 21316, 23597, 9570, 30451, 24496, 3625, 13742, 3919, 18140, 25573, 32442, 20843, 29896, 22881, 19590, 6471, 5492, 10909, 11026, 739, 5344, 21401, 26206, 27199, 7948, 4181, 2666, 27483, 8184, 23761, 25398, 25143, 17316, 29965, 31938, 27347, 30224, 21769, 8974, 24879, 25404, 14533, 25114, 24907, 30504, 7233, 1510, 18215, 24020, 15229, 6770, 11971, 832, 4729, 27582, 29727, 4972, 23861, 1482, 13115, 31320, 6065, 13462, 18455, 25604, 32237, 1058, 20147, 15472, 3049]

Podemos cambiar el orden de los parámetros si especificamos quienes son

# Ambas son equivalentes a print(aleatorios(n=5, seed=83984, ...)) 
print(aleatorios(n=5,seed=83984))
print(aleatorios(seed=83984, n=5))

[16137, 17678, 23343, 21820, 17093]
[16137, 17678, 23343, 21820, 17093]

Listas de funciones

Las funciones en python son objetos y se pueden manipular como cualquier otro objeto: colocarse en listas o en diccionarios.

Esto es util cuando la función que usaremos para una tarea es en si un parámetro del método.

def func1():return 1
def func2():return 2
def func3():return 3

funclist = [func1,func2,func3]

a=funclist[0]()
b=funclist[1]()
c=funclist[2]()

a,b,c

(1, 2, 3)

x = [f() for f in funclist ]
x

[1, 2, 3]

Diccionarios de funciones

funcdict = {'f1':func1,'f2':func2,'f3':func3}

x = [funcdict[f]() for f in funcdict ]
print(x)

funcdict

[1, 2, 3]





{'f1': <function __main__.func1>,
 'f2': <function __main__.func2>,
 'f3': <function __main__.func3>}

Modulos (Librerías)

Uso de librerias para cómputo científico en Python

Importar un módulo completo

import mod-name

Importar un módulo completo y darle un nombre simplificado

import mod-name as alias

**Importar solo un componente de un módulo **

from mod-name import mod-component

**Importar solo un componente de un módulo y darle un alias **

from mod-name import mod-component as alias

El módulo math para acceso a funciones de biblioteca en C de punto flotante

Python es un lenguaje que soporta probramación orientada a objetos (POO)

Los componentes se invocan usando la notación modulo.componente

import math

math.<…>

import math
c = math.cos(math.pi / 4) 
s = 1/math.sqrt(2)
l = math.log(1024, 2)
print(c,s,l)

0.7071067811865476 0.7071067811865475 10.0

El módulo random proveé funciones para acceso y generación de números aleatorios

import random as rnd
name= rnd.choice(['Juan', 'Pedro','Elsa','Ana', 'Alberto','Judith',
                  'Miguel', 'Oscar','Laura', 'Jose', 'Roberto', 
                  'Andres', 'Maria'])

smpl = rnd.sample(range(100), 20)   # muestreo sin reemplazo 

print(name)
print(smpl)

Oscar
[31, 15, 94, 4, 76, 9, 26, 89, 54, 29, 79, 12, 44, 10, 41, 73, 90, 65, 63, 47]

El módulo statistics proveé funciones para cálculo de estadísticos

import statistics
data = [65, 91, 37, 72, 63, 41, 82, 31, 17, 47, 76, 
        64, 70, 83, 26, 30, 92, 84, 95, 21]

print('media =', statistics.mean(data))
print('mediana =', statistics.median(data))
print('varianza =', statistics.variance(data))

media = 59.35
mediana = 64.5
varianza = 666.6605263157894

El módulo os permite acceso a commandos del sistema asi como a configuración de stderr, stdin , stdout

import os
print(os.getcwd())      # Return the current working directory
print(os.system('ls'))  # consulte su terminal !

/Users/marianoriverameraz/Documents/cursos/learning/DLnotas/0 MLnotas_bck/0 Revisión/1 Python
0

!ls .

[31mLogoCNS_IPICYT.png[m[m       [31mfuncionesSets.png[m[m        [31mscipy_org_logo.gif[m[m
[31mPyhon1.ipynb[m[m             [34mpara_Material[m[m            [31mslicing_python.png[m[m
[31mPython2.ipynb[m[m            [31mpythonLogo.png[m[m           [31mtest_prolog.ipynb[m[m
[31macuse.pdf[m[m                [31mpython_ejercicios1.ipynb[m[m [31mtsukuba_rsz.png[m[m
cimat_logo.png           rbfInt.py                [31mtsukubita.png[m[m
[34mcs228-material-master[m[m    [31ms.png[m[m

Módulos Cómunes para Cómputo Científico y Aprendizaje de Máquina

numpy (np): **Libería básica para calculos numéricos **

scipy (sp): Libería para cómputo científico, construye sobre numpy

matplotlib (mpl): Libería para graficación de datos

sklearn (skl): Librería con funciones de aprendizaje de máquina

pandas (pd): ** Libreria para acceso a datos **

Modulo Matplotlib

Matplotlib es un librería para graficación. Veremos un introducción al módulo Marplotlib.pyplot que permite hacer ‘plots’ de funciones.

%matplotlib inline

este comando permite que las graficas se muestren en el notebook y no en ventanas separadas

numpy

es la libreraia básica numérica de python, la veremos despues mas a detalle

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

# Compute the x and y coordinates for points on a sine curve
theta = np.arange(-2*np.pi, 2*np.pi, 0.1)
y = np.sin(theta)

# Plot the points using matplotlib
plt.plot(theta, y)

# Desplegamos la figura
plt.show()

png

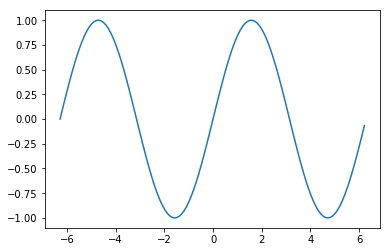
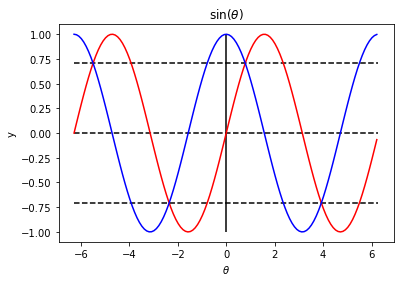
Agregardole Titulo, leyenda a cada eje, algunas lineas guias, cambiando colores de trazos y estilos.

plt.plot(theta, y, color='r')
plt.plot(theta,np.cos(theta), color='b')
plt.title(r'$\sin(\theta)$')
plt.xlabel(r'$\theta$')
plt.ylabel('y')
plt.hlines(y=[-.7071,0,0.7071], xmin=-2*np.pi, xmax=2*np.pi, 
           colors='k', linestyles='dashed')
plt.vlines(x=0, ymin=-1, ymax=1, colors='k', linestyles='solid')
plt.show()

png

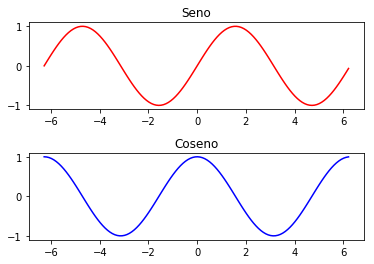
Subplots

Múltiples plots a la vez

# calulamos ek seno y coseno 
x = np.arange(-2*np.pi, 2 * np.pi, 0.1)
sx = np.sin(x)
cx = np.cos(x)

# Activamos subplost arrglados de 
# (alto, ancho, indice del activo)
plt.subplot(2, 1, 1)
plt.plot(x, sx, color='r')
plt.title('Seno')

#  Activamos el segindo subplot
plt.subplot(2, 1, 2)
plt.plot(x, cx, color= 'b')
plt.title('Coseno')

# ------------------------
# Desplegamos la figura
# ------------------------
hspace = 0.5  # Espacio entre subplots, lo incrementamos.
plt.subplots_adjust(hspace=hspace)
plt.show()

png

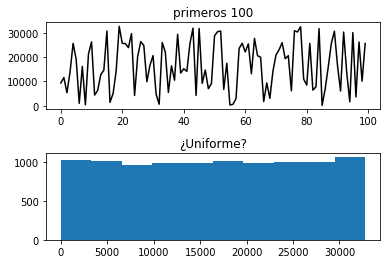
x = aleatorios(n=10000)  # funcion definida arriba!

# podemos obviar las comas si los indices son menores a 10
plt.subplot(211)
plt.title('primeros 100')
plt.plot(x[:100], color='k')

plt.subplot(212)
plt.title('¿Uniforme?')
plt.hist(x)

# ------------------------
hspace = 0.5  # Espacio entre subplots, lo incrementamos.
plt.subplots_adjust(hspace=hspace)
plt.show()

png

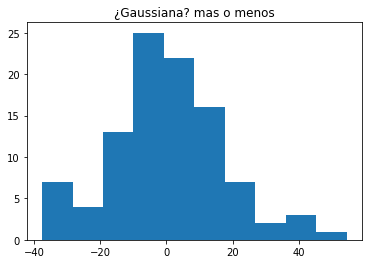
¿Como generamos datos con distribución Gaussiana?

Useremos el teorema del límite central.

# ---------------------------------------------------
def generaUniforme(n=10, a=0, b=1,):
    import time
    s = time.time()
    seed=int((s-int(s))*100000)
    return (np.array(aleatorios(n=n, seed=seed))/32768*(b-a)+a)

# ---------------------------------------------------
def generaGaussianos(K=100, n=10, mean=0, sigma=1):
    '''
        n     tamaño dekl vector de numeros gaussianoss a generar
        mean  media todos los gaussianos
        sigma desviacion std de los gaussiano
        K     numero de numeros con distrobuicion uniiforme a generar para 
              generar un gaussiano (se usa el Teoriem del limite central)
    '''
    x = generaUniforme(n=100, a=-1,b=1)
    for i in range(K):
        x += generaUniforme(n=100, a= -1,b=1)
    
    return sigma*x+mean
# ---------------------------------------------------

x = generaGaussianos(K=1000, n=10000, mean=0, sigma=1)
plt.title('¿Gaussiana? mas o menos')
plt.hist(x)
plt.show()

np.std(x)

png

17.435306121264293

Método de Montecarlo para calcular PI

Área de un círculo:
$A_c = \pi r^2$

Área de un cuadrado:
$A_s = l^2$

Si, hacemos un círculo de radio $r=1$ y lo inscribimos en un cuadrado de lado $l=2$ . La relación entre las áreas es

$\frac{A_c}{A_s} = \frac{\pi}{4}$

Entonces, la probabilidad de que el vector bi-valuado con entradas con distribución uniforme $[-1,1]$ tenga magnitud menor o igual a 1 es $\pi / 4$ .

n = 1000000
x =generaUniforme(n=n, a= -1,b=1)
y =generaUniforme(n=n, a= -1,b=1)
r = np.array([x,y])
r_nrm = np.linalg.norm(r,axis=0) 
mi_pi = 4*np.sum(r_nrm<=1)/n
print (np.pi, ' vs ', mi_pi)

3.141592653589793  vs  3.141968

Scipy

Es una libreria de mayor nivel que numpy.

Cuenta con módulos para leer imagenes

from scipy.misc import imread, imsave, imresize

# leer una imagen en png con canal alpha!
img = imread('./tsukubita.png')

# cambia la imagens a tonos de gris, sumando los 
# canales [red green blue alpha]
img_gray = np.sum(img,2)
# cambia de dimensiones con interpolación bicubica
img_gray = imresize(img_gray, (500, 500), interp='bicubic')

# Escribe la imgen en gris en el disco
imsave('tsukuba_rsz.png', img_gray)

# despliega la imagenes
plt.subplot(121)
plt.imshow(img)
plt.subplot(122)
plt.imshow(img_gray, cmap='gray')
plt.show()

png

Módulos para transformada de Fourier Scipy

En numpy existe el módulo numpy.fft

Sin embargo la libreria de Scipy es mas completa e inclusive tienen transformadas cosenos y seno de diferentes tipos

Transformada Directa y Discreta de Fourier Discreta
$X_u = \sum_{k=0}^{k=n-1} x_k \exp \left(-\frac{2 \pi k u}{n} \right)$

Transformada Inversa y Discreta de Fourier
$x_k = \frac{1}{n}\sum_{u=0}^{u=n-1} X_u \exp \left(\frac{2 \pi k u}{n} \right)$

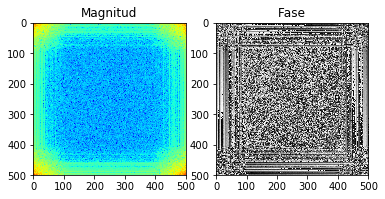
from scipy.fftpack import fftn
I = fftn(img_gray) # transformada directa

# se usa el log para propositos de visualización
plt.subplot(121)
plt.imshow(np.log(np.abs(I)), cmap='jet')
plt.title('Magnitud')
plt.subplot(122)
plt.imshow(np.angle(I), cmap='gray')
plt.title('Fase')
plt.show()

png