Gradiente Proyectado Descafeinado

Mariano Rivera

octubre 2018

Programas cuadráticos con restricciónes de cota

Los programas cuadráticos con restricciónes de cota (Bounded Quadratic Programming, B-QP) son problemas de optimización con restricciones [1]. Éstos son populares en problemas en tareas relacionadas con reconocimietno de patrones, aprendizaje de máquina, procesamiento de imágenes y visión por computadora. Su forma general es

(1)
arg⁡min⁡x12x⊤H x−d⊤x            s.a.      l⪯x⪯h \underset{x}{\arg \min} \frac{1}{2} x^\top H\, x - d^\top x \\ \;\;\;\;\;\; \text{s.a.} \;\;\; l \preceq x \preceq h
donde HH es una matriz Hessiana (simétrica), ll y hh son vectores de iguales dimensiones que xx y definen la cota inferior y superior de los valores válidos para xx. El conjunto de puntos válidos definen la región factible Ω\Omega.

[1] De Angelis P.L., Toraldo G. (2008) Quadratic Programming with Bound Constraints. In: Floudas C., Pardalos P. (eds) Encyclopedia of Optimization. Springer, Boston, MA

Ejemplos de programas cuadráticos con restricciónes de cota

Mínimos Cuadrados no Negativos (NNLS)

(2)
arg⁡min⁡x12∥A x−b∥2            s.a.      x⪰0 \underset{x}{\arg \min} \frac{1}{2} \|A\,x-b \|^2 \\ \;\;\;\;\;\; \text{s.a.} \;\;\; x \succeq 0

En este caso tenemos que

(3)
∥Ax−b∥2=(A x−b)⊤(A x−b)=x⊤A⊤A x−A⊤b x \|Ax-b \|^2 = (A\,x-b)^\top (A\,x-b) = x^\top A^\top A \, x - A^\top b \, x
por lo que (2) equivale a la forma (1) con H=A⊤AH = A^\top A, d=A⊤bd = A^\top b, l=0l=0 y h=∞h =\infty.

Casos de problemas de NNLS son los problemas de Persecusión de Bases (Basis Pursuit). En estos problemas se cuenta con un diccionario de funciones {fi}i=1,2,…,n\{f_i\}_{i=1,2,\ldots,n} y se busca encontrar la combinación lineal (suma pesada-positiva) de dichas funciónes para ajustar una señal b∈Rmb \in \mathbb{R}^m. Generelmente el diccionario es sobredeterminado (tenemos mas funciones componentes que variables en bb:   m>n\;m>n) por lo que el prolema debe ser regularizado:

(4)
arg⁡min⁡x12∥A x−b∥2+λ∥x∥2            s.a.      x⪰0 \underset{x}{\arg \min} \frac{1}{2} \|A\,x-b \|^2 + \lambda \| x\|^2 \\ \;\;\;\;\;\; \text{s.a.} \;\;\; x \succeq 0
donde las columnas de A son las funciones {fi}\{f_i\}, (A=[f1,f2,…,fm,]A= \left[ f_1, f_2, \ldots, f_m,\right]), λ\lambda es un parámetro de penalización (regularización Ridge) que promueve que usar pocas funciones para en solución.

Para mas sobre regularización de paramétros por contracción (shrinkage), ver Regularización Ridge, LASSO y ElasticNet.

[2] D. Donoho, I. Johnstone, J. Hoch, and A. Stern. Maximum entropy and
the nearly black object. Journal of the Royal Statistical Society Series B,
54:41–81, 1992.

[3] D. Kim, S. Sra, and I. Dhillon. Tackling box-constrained convex opti- mization via a new projected quasi-Newton approach. SIAM Journal on Scientific Computing, 32:3548–3563, 2010.

Factorización no negativa de matrices (NNMF)

Sea A∈Rm×nA \in \mathbb{R}^{m \times n} una matrix de rango k=min⁡{m,n}k = \min\{m,n \} con todos sus componentes no-negativos: A⪰0A \succeq 0. Entonces AA puede factorizarse como el producto de dos matrices nonegativas [4]:

(5)
A=W H A = W \, H

con W∈Rm×kW \in \mathbb{R}^{m \times k} y H∈Rk×nH \in \mathbb{R}^{k \times n}. La factorización se obtienen resolviendo
(2)
arg⁡min⁡W,H12∥A−W H∥2            s.a.      W,H⪰0 \underset{W,H}{\arg \min} \frac{1}{2} \|A - W \,H \|^2 \\ \;\;\;\;\;\; \text{s.a.} \;\;\; W,H \succeq 0
Note que este problema es no cuadrático debido al producto entre las incógnitas. Si no se conoce kk o se predende calcular una factorización mas comprimida, entonces se propone una valor para kk mediante la solución de (2) obtenemos una buena aproximación.

Importantes propiedades de NNMF han sido reportadas en [5,6]

[5] C. Ding et al. On the equialence of nonnegative matrix factorization and spectral clustering, Proc. SIAM Int. Conf. Data Mining, 2005

[6] M. Slawski and M. Matthias. Non-negative least squares for high-dimensional linear models: Consistency and sparse recovery without regularization. Electron. J. Statist. 7 (2013), 3004–3056. doi:10.1214/13-EJS868.

Máquinas de Vectores de Soporte (SVM)

Sea xi∈Rn{x_i} \in \mathbb{R}^n un vector que corresponde al ii-ésimo dato tal que la jj-ésima entrada xij{x}_{ij} corresponde a la jj-ésima característica. Luego arreglamos los datos de la forma

X=[x1⊤x2⊤⋮xm⊤], X = \begin{bmatrix} {x}^\top_1 \\ {x}^\top_2 \\ \vdots \\ {x}^\top_m \\ \end{bmatrix}, \\
de tal que cada dato corresponde a un renglón de la matrix X∈Rm×nX \in \mathbb{R}^{m \times n} y tenemos una etiqueta yi∈{−1,1}y_i \in \{-1, 1\} asociada a cada dato. LA etiqueta indica la clase a que pertenece. Luego denotamos el vector de etiquetas por

y=[y1y2⋮ym], y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \\ \end{bmatrix},\\

La SVMs para clasificación binaria se formulan como un QP con resticciones de cota y una restricción de igualdad. El problema a resolver esta dado por

(6)
arg⁡min⁡s12v⊤Ks−1⊤s            s.a.      y⊤s=00⪯s⪯C \underset{s}{\arg \min} \frac{1}{2} v^\top {\bf K} s - {\bf 1}^\top s \\ \;\;\;\;\;\; \text{s.a.} \;\;\; y^\top s = 0 \\ 0 \preceq s \preceq C
donde K{\bf K} es una matrix semidefinida positiva con elementos dados por

(7)
[K]ij=yi yj xi⊤xj \left[{\bf K} \right]_{ij} = y_i \, y_j \,x_i^\top x_j
para el caso de clases linelamente separables y

(8)
[K]ij=yi yj K(xi,xj) \left[{\bf K} \right]_{ij} = y_i \, y_j \, K(x_i, x_j)
para el caso de clases no-linelamente separables, donde KK es una función Kernel qel mapeo de datos xx's a un espacio de mayor dimensión: K(p,q)=ϕ(p)⊤ϕ(q)K(p,q) = \phi(p)^\top \phi(q); espacio donde se espera que las clases sean linelamente separables. Finalmente CC permite hacer la clasificación robusta a outliers. En el caso en que las calses sean estrictamente linealmente separables C=∞C= \infty; es decir no hay restricción de cota superior.

Para más sobre SVMs ver la siguiente liga, el artículo original [7], el tutorial [8].

[7] Cortes, C. & Vapnik, V. (1995). Support-vector network. Machine Learning, 20, 1–25.

[8] M.A. Hearst et a., Support vector machines, IEEE Int. Syst., 13(4), pp. 18-28 , 1998, DOI: 10.1109/5254.708428.

El Gradiente Protectado como Motivación

[5] J. Nocedal and S. Wright, Numerical Optimization, 2nd Ed. Springer, 2006.

El algoritmo de gradiente proyectado puede entenderse a partir de la siguiente figura.

En el panel (a) se asume que iniciamos en un punto actual xtx^t dentro de la región factible (región rectangular en verde). Si usamos una estrategia de máximo descenso, sin considerar las restricciones, entonces el paso estaría definido por −α gt.-\alpha\, g^t. Sin embargo el nuevo punto xt−α gtx^t - \alpha \, g^t no sería factile. Para evitar ello, el paso (gradiente con tamaño de paso) es proyectado a la región factible usando

P(z;l,h)={lizi<lihizi>hiziotro P(z;l,h) = \left\{ \begin{matrix} l_i & z_i < l_i \\ h_i & z_i > h_i \\ z_i & \text{otro} \end{matrix} \right.

El paso proyectado forma un camino recto a pedazos como lo muestra el Panel (b). Sobre el camino proyectado se busca el primer mínimo mediante una inspeción de tramo por tramo. El primer mínimo se muestra en el Panel © que es el lugar en que el camino proyectado es tangente a una curva (o superficie) de nivel.

El algoritmo de Gradiente Proyectado tienen un paso más que mejora su convergencia. Una vez que se determina el primer mínimo en lo largo del camino proyectado, se fijan las variables que han activado restricciones (denominadas variables activas) y se procede a minimizar, aproximadamente, en el sub-espacio definido por las variables no activas.

Decaf Gradiente Protectado

Cuando nos referimos a la versión descafeinada de un algoritmo nos referimos a una versión más fácil de implementar y, si bien es tan eficiente en términos de convergencia que la versión original, si grantiza convergencia a la solución. Una versión DECAF puede ser muy útil para desarrollar prototipos; en la etapa en que aun estamos haciendo pruebas a nuestros modelos.

El Gradiente Proyectado Descafeinado se ilustra en la siguiente figura.

La estrategia de gradiente proyectado re resume en iterar:

Mas formalmente lo implementamos como sigue:

Sea m=1m =\mathbf{1} un vector con unos en todas sus entradas y de las mismas dimensiones que θ\theta, luego

Iterar los siguientes pasos hasta convergencia

  1. Calcular el gradiente de la función objetivo

  2. Calcular la dirección de descenso: p=−gp=-g

  3. Reinicializar mm cada kk iteraciones:
    if t%k==0: m=1

  4. Actualizar los parámetros
    θt+1=θt+α∗m⊙p \theta^{t+1} = \theta^t + \alpha * m \odot p
    donde ⊙\odot es el producto elemento a elemento (producto de Hadamard: x⊙y=[x1y1,x2y2,…]⊤x \odot y = [x_1 y_1, x_2 y_2, \ldots]^\top).

  5. Detectar los índices de las entradas que violan la restricción:
    Ω={i:θi<0} \Omega = \{ i : \theta_i <0\}

  6. Recortar (Clipping) las variables que se salen de la región factible: ∀i∈Ω\forall i \in \Omega hacer θi=0\theta_i=0

  7. Recortar mm: ∀i∈Ω\forall i \in \Omega hacer mi=0m_i=0

Ejemplo 1: Aproximación mediante NN-RBF

Dada la función suave

yi=sin⁡(xi7)+2 cos⁡(xi−7020)+c y_i = \sin\left(\frac{x_i}{7}\right) + 2\, \cos \left(\frac{x_i-70}{20}\right) + c
donde cc es una constante que hace que y⪰0y \succeq 0 y xi=ix_i = i para i=0,1,2…,ni = 0,1,2 \ldots, n; con n=100n=100

Resolver
arg⁡min⁡θ  ∥Φθ−y∥2              s.a.    θ≥0 \underset{\theta}{\arg \min } \; \| \Phi \theta - y \|^2 \\ \;\;\;\;\;\;\; s.a. \;\; \theta \ge 0
donde

Φ=[ϕ0,ϕ2,…,ϕm]\Phi = [\phi_0, \phi_2, \ldots, \phi_m]

es un diccionario de funciones base
y ϕj\phi_j es el jj-ésimo átomo (función base), que es un vector columna y se define por

ϕi=exp⁡(−x−μi2σ2) \phi_i = \exp\left(-\frac{x-\mu_i}{2\sigma^2} \right) 

import numpy as np
import matplotlib.pyplot as plt

x = np.array(range(100))

def f(x):
    y=np.sin(x/7)+2.*np.cos((x-70)/20)
    return y-np.min(y)

def gss(x, media, s):
    return np.exp(-(x-media)**2/(2.*s**2))

def calculaPhi(x, numRBF=10, sigma=6):
    ndata=len(x)
    paso = np.ceil(ndata/numRBF)
    medias = np.arange(0,ndata+paso,paso)
    Phi=[]
    for media in medias:
        phi= gss(x,media,sigma)
        Phi.append(phi)
    return np.array(Phi).T

def calculaGradf(y, Phi, theta):
    grad = Phi.T@(Phi@theta-y)
    return grad

# señal
y=f(x)
# Diccionario

Phi=calculaPhi(x=x, numRBF=12, sigma=6)

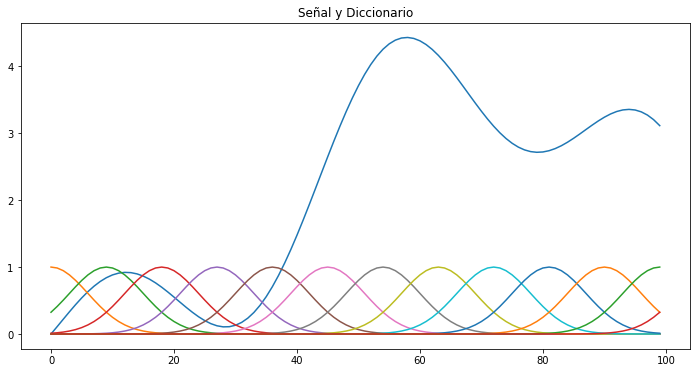
Deiccionario y función a aproximar

plt.figure(figsize=(12,6))
plt.plot(y)

n,m= Phi.shape
for i in range(m):
    plt.plot(Phi[:,i])

plt.title('Señal y Diccionario')
plt.show()

png

Desceso de gradiente simple sin restricciones

N=100
theta = np.ones(m)
alpha=0.01
for i in range(N):
    grad = calculaGradf(y, Phi, theta)
    theta=theta-alpha*grad

print('grad=\n', grad)
print('theta=\n', theta)

plt.figure(figsize=(12,6))
plt.plot(y, 'r')
for i in range(m):
    plt.plot(theta[i]*Phi[:,i])

haty= Phi@theta
plt.plot(haty, 'go')
plt.title('Approximación RBF')
plt.show()

grad=
 [ 0.15576335 -0.13285693  0.06640374 -0.00863362 -0.01732008  0.01881689
 -0.01368835  0.0102288  -0.00404902 -0.01093976  0.03037573 -0.03781717
 -0.00632543]
theta=
 [-0.07728272  0.6386445   0.57739821 -0.17022554  0.1908662   1.63681606
  2.84901629  2.64892047  1.72460445  1.43476044  2.09451563  2.04728421
  1.17367164]

png

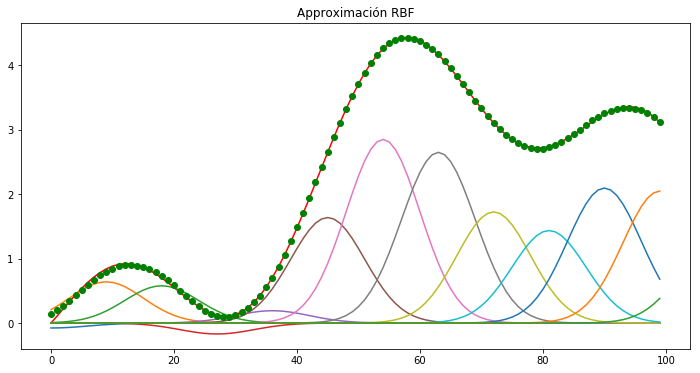
Como podemos observar, la aproximación (puntos verdes) se ajusta muy bien a la función original (línea roja)

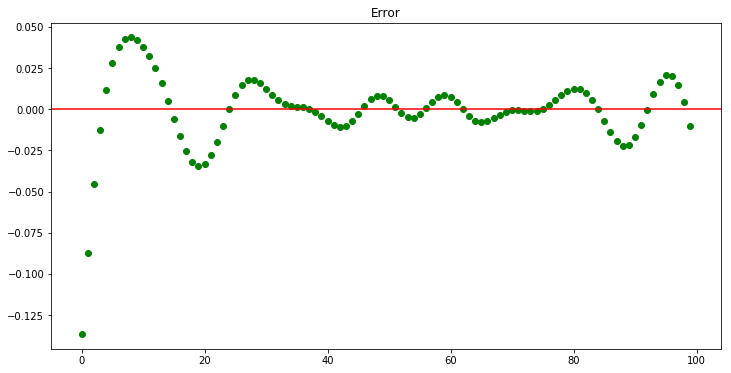
En la siguiente figura desplegamos el error en cada punto.

plt.figure(figsize=(12,6))
plt.plot(y-haty, 'go')
plt.axhline(y=0, color='r', linestyle='-')
plt.title('Error')
plt.show()

png

Descenso de gradiente proyectado descafeinado

Ahora la implementación del GP-Decaf para NN-RBF

N=300
theta = np.ones(m)
alpha=0.01

msk = np.ones(theta.shape) 

K=10
for i in range(N):
    grad = msk*calculaGradf(y, Phi, theta)
    theta=theta-alpha*grad
    # proyeccion
    msk[theta<0]=0
    theta[theta<0]=0
    if i%K==0:
        msk = np.ones(theta.shape) 
        
print('norma del grad=\n', grad@grad)
print('theta=\n', theta)


plt.figure(figsize=(12,6))
plt.plot(y, 'r')
for i in range(m):
    plt.plot(theta[i]*Phi[:,i])

haty= Phi@theta
plt.plot(haty, 'g*')
plt.title('')
plt.show()

norma del grad=
 0.000127934053097
theta=
 [ 0.          0.65809328  0.46698228  0.          0.0736745   1.70112498
  2.81665557  2.66632238  1.71049321  1.45282892  2.07062272  2.07227976
  1.16924487]

png

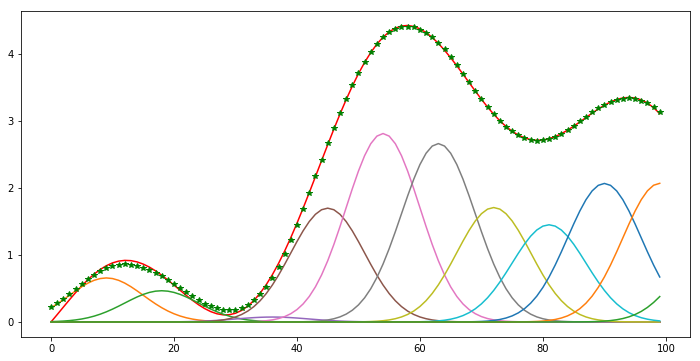
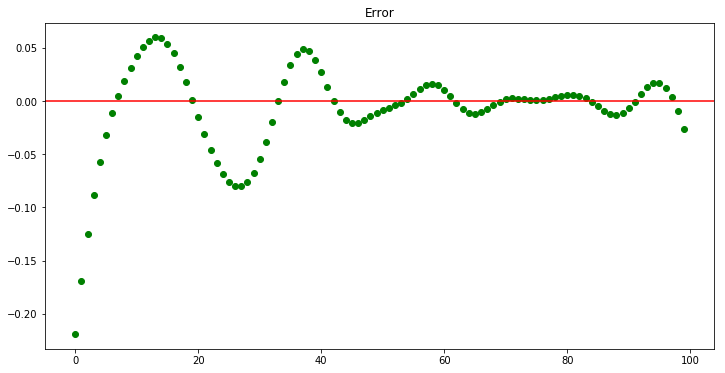
Note que no hay valores negativos en los coeficientes calculados, de hecho la solución no negativa requiere de 2 (ver los zeros) funciones base menos que la no retringida. Los errores se concentran al inicio donde la estimación esta por arriba de los datos y no es posible reducir la aproximación sin usar coeficientes negativos.

plt.figure(figsize=(12,6))
plt.plot(y-haty, 'go')
plt.axhline(y=0, color='r', linestyle='-')
plt.title('Error')
plt.show()

png

Ejemplo 2: SVMs

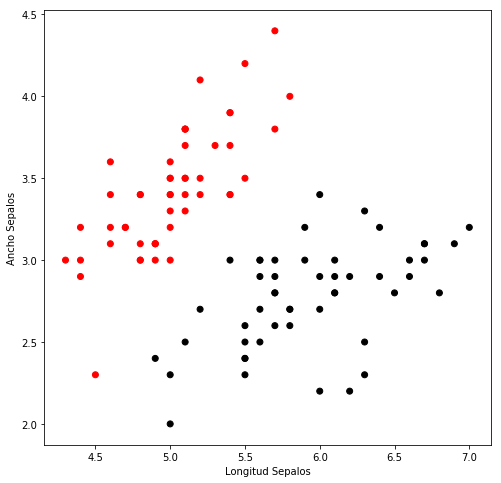
En este ejercicio entrenaremos una máquina de vectores de soporte para clasificación binaria de las dos primeras clases ({0,1}\{0,1\}) de la base de datos IRIS.

La base de datos IRIS esta diponible en el paquete de python scikit-learn y consta de 4 clases, de las cuales seleccionamos las dos primeras, cada datos consta de 4 rasgos medidos a flores iris:

  1. Largo del sépalo
  2. Ancho del sépalo
  3. Largo del pétalo
  4. Ancho del pétalo

Se seleccionaron esas clases y rasgos por ser en el linealmente separables como se muestra en los puntos gráficados.

La estrategia utilizada es optmizar el Lagrangiano Aumentado [5] con la restricción de igualdad y con Decaf Gradiente Proyectado se implementa la restricción de cota (no-negatividad).

Lectura de los Datos

%matplotlib inline

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn import datasets

iris = datasets.load_iris()

print("llaves :", iris.keys())
print('número de muestras :', iris['data'].shape[0])
print('número de caractéristicas : ', iris['data'].shape[1])

llaves : dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])
número de muestras : 150
número de caractéristicas :  4

idx= iris.target<2        # primeras dos clases
y= iris.target[idx]   
y =2*y -1                 # {-1, 1}
#-[1]                     # cambiamos a un dato su etiqueta
x  = iris.data[idx, :2]   # primeras dos características

plt.figure(figsize=(8, 8))
plt.scatter(x[:, 0], 
            x[:, 1], 
            c=Y, 
            cmap=plt.cm.flag)
plt.xlabel('Longitud Sepalos')
plt.ylabel('Ancho Sepalos')
plt.show()

png

Lagrangiano y su gradiente

def LagrangianAug(Q, y, theta, Lambda, rho):
    return 0.5* theta.T@Q@theta - np.sum(theta) - Lambda*constricc + 0.5*rho* constricc**2

def gradLagrangianAug(Q, y, theta, Lambda, rho):
    return Q@theta - 1.0 - (Lambda - rho*y.T@theta)*y
    
theta  = np.ones(y.shape)

nIter=150000
alpha=0.001
if y.shape !=(100,1):
    y= np.expand_dims(y, axis=1)
    
Lambda = 1.0
rho = 1/1000.
theta  = np.ones((x.shape[0],1))
msk = np.ones(theta.shape) 

K=5
Q = (y*x)@(y*x).T
for i in range(nIter):
    grad = msk*gradLagrangianAug(Q=Q, y=y, theta=theta, Lambda=Lambda, rho=rho)
    theta=theta-alpha*grad
    # proyeccion
    msk[theta<0]=0
    theta[theta<0]=0
    if i%K==0:
        msk = np.ones(theta.shape) 
        if rho<100:
            rho*=1.01
        Lambda=Lambda-rho*y.T@theta

print('norma del grad=\n', grad.T@grad)


norma del grad=
 [[ 0.00838404]]

Valor de la restricción de igualdad

np.sum(y*theta)

-6.7296752614964817e-09

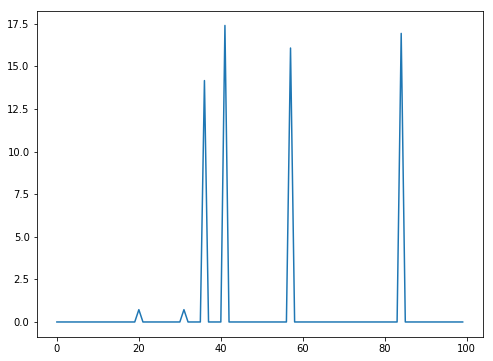
Valor de los multiplicadores de Lagrange que indican los vectores soporte detectados

plt.figure(figsize=(8,6))
plt.plot(theta)
plt.show

<function matplotlib.pyplot.show>

png

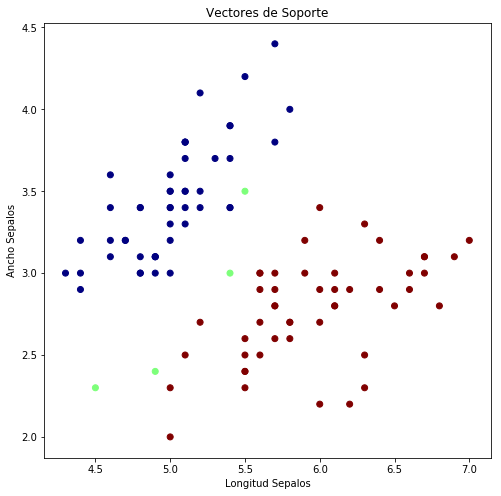
idx = theta>5.0
y[idx]=0
plt.figure(figsize=(8, 8))
plt.scatter(x[:, 0], 
            x[:, 1], 
            c=(y[:,0]+1.0)/2.0, 
            cmap=plt.cm.jet) 
plt.xlabel('Longitud Sepalos')
plt.ylabel('Ancho Sepalos')
plt.title('Vectores de Soporte')
plt.show()

png

Ejercicio 1. Implementar NNMF usando decaf-pg

Ejercicio 2. Implementar la versión decaf-nesterov para el problema de SVM