Autocodificadores Variacionales

(Variational Autoencoders, VAEs)

Mariano Rivera

Diciembre 2018

Ejemplo tomado del capítulo 2 de (Lagr and Bok, 2019).

Los autoencoders variacionales (VAEs) son una estrategia que ha demostrado se muy exitosa para aprender en forma no supervisada distribuciones complejas de datos.

Los VAEs han permitido generar datos complejos, por ejemplo

Números manuscritos (ejemplo desarrollado en esta notas) (Kingma and Welling, 2014)
Rostros humanos (Kingma and Welling, 2014, Jimenez-Rezende et al, 2014).
Segmentación de imágenes (Sohn et al, 2015).

Modelos predictivos

Suponga el problema de reconocimiento de rostros, donde dado un vector de datos (imagen) $x_i$ en el conjunto de imágenes $X$ , la tarea es clasificar a $x_i$ entre rostro humano o no-rostro humano. Es decir, deseamos estimar el valor de la etiqueta asociada $y_i \in \{0,1\}$ , con $1$ que significa “si rostro” y $0$ que significa “no rostro”.

En vez de tratar de calcular directamente la etiqueta, lo que nos llevaría a un problema combinatorio, un más enfoque práctico es calcular la probabilidad de que $x_i$ sea la imagen de un rostro:

(1)
$P(x_i) \overset{def}{=}P(y_i=1 | x_i) \in [0,1]$

de esta manera, la probabilidad de que la imagen sea un “no-rostro” es $P(y_i=0 | x_i) = 1-P(x)$ .

Primero, lo que notamos es que contamos con un conjunto de $m$ imágenes (denotado por $X$ ) de las cuales conocemos sus etiquetas $Y$ . Es decir, es nuestro problema es del tipo aprendizaje supervisado.

Las imágenes han sido organizadas de la siguiente manera:

(2)
$X = \begin{bmatrix} x_1^\top \\ x_2^\top \\ \vdots \\ x_m^\top \\ \end{bmatrix}$
donde el reglón $i$ -ésimo de $X$ , y el vector $x_i \in \mathbb{R}^n$ es un vector donde los renglones de la matriz de han puesto tras otro ( $n=$ num_renglones $\times$ num_columnas), como lo hace la Capa (layer) Flatten de Keras.

También asumimos que para reducir los efectos de iluminación o tono de piel, cada rostro fue normalizado usando

(3)
$x_i \leftarrow \frac{(x_i - mean(x_i) )}{std(x_i)}$

es decir, a cada renglón se le substrajo la media y se le dividió entre su desviación estándar.

Por otro lado las etiquetas asociadas se han organizado en el vector

(4)
$Y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \\ \end{bmatrix}$

El primer problema que afrontamos es ¿cómo definir esta probabilidad $P(x)$ ?

Se nos ocurren inicialmente dos estrategias:

Estos métodos son útiles para para dadad una imágen $x$ estimar la probabilidadd de que dicha imagen es un rostro, pero no para generar datos sintéticos que no hayan sido vistos por el método. No no permiten construir generadores de datos sintéticos complejos.

Modelos Generativos

Ahora, consideremos que no solo queremos aprender la distribución subyacente de los datos para hacer inferencia sobre datos no vistos (evaluar la probabilidad de que una nueva imagen sea o no un rostro), sino que queremos generar muestras de (muestrear) dicha distribución. Es decir, queremos generar imágenes que sean muy parecidas a rostros, imágenes que no han sido vistas antes en el proceso de entrenamiento. Para esta nuevo problema, los modelos predictivos son útiles para indicar que tan parecida es una imágen a un rostro no son necesariamente útiles para sintetizar imágenes de rostros.

Si nuestros datos $x$ (en la base de datos $X$ ) se distribuyen de acuerdo a la distribución verdadera $\hat P(x)$ , el próposito es ahora, estimar una distribución $P(X)$ que podamos muestrear y que sea lo mas similar posible a $\hat P(x)$ .

Este problema de aprendizaje de máquina es de gran interés para la comunidad de aprendizaje, sin embargo las estrategias usadas, generalmente, tienen las siguientes limitantes:

Construyen sobre suposiciones muy estrictas de la distribución verdadera $\hat P$ . Por ejemplo, que sigue una forma paramétrica simple y/o monomodales, o son mezclas de ellas con un límitado número de modas.
Hacen aproximaciones muy fuertes sobre la estructura de los datos. Por ejemplo, el que las correlaciones entre las entradas son lineales.
Para su cálculo se require el uso de métodos numéricamente costosos como Monte Carlo para Cadenas de Markov (MCMC).

Recientemente se ha propuesto un método llamado Autocodificadores Variacionales (VAN) para estimar distribuciones. En los VANs, las suposiciones sobre las distribuciones son relajadas considerablemente y son entrenables mediante backpropagation (BP); con todas las ventajas de paralelización y entrenamiento por lotes de BP.

Para mas información sobre VAEs, recomendamos el tutorial de (Doersch, 2016) y el (Blog de Altosaar)

Variables Latentes

El ejemplo que usaremos es el de generar imágenes de dígitos manuscrito a partir de los ejemplos en la BD MNIST.

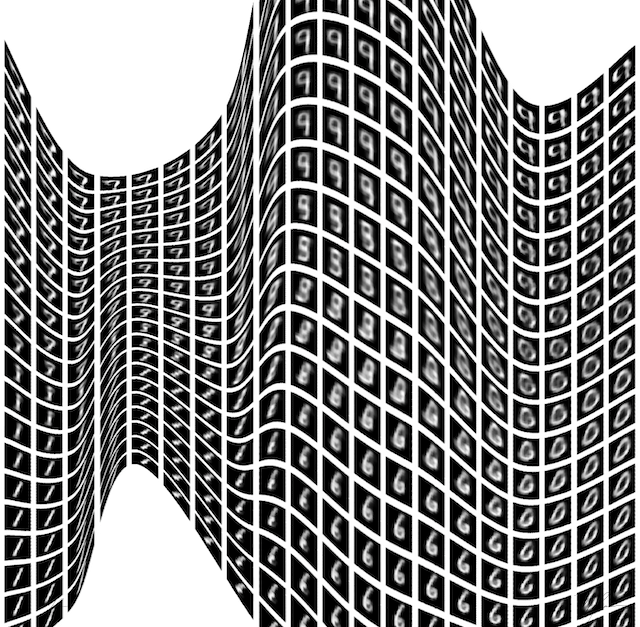
La idea clave en los autoencoders variacionales es que nuestros datos, aunque sean de muy altas dimensiones ( $28 \times 28 = 784$ pixeles), en realidad “viven” en un espacio de baja dimensión el cual es parametrizado por el vector $z$ ; que, como digimos, es de baja dimensión. Este vector $z$ es la variable latente y codifica la información para generar las imágenes. Variando $z$ generamos los distintos dígitos con sus distintos estilos.

Como dato, el número de posibles imágenes de $32 \times 32$ pixeles, cada pixel en colores RGB con 256 posibles valores es

$\left(\underbrace{256}_{R} \times \underbrace{256}_{G} \times \underbrace{256}_{B}\right)^{\overbrace{32 \times 32}^{pixeles}} = \left(\underbrace{2^{24}}\right)^{{32 \times 32}} = 2^{24576} \approx 10^{7398}$

es un número realmente grande, se estima que el número de átomos en el universo es de tan solo de $10^{82}$ .

bend

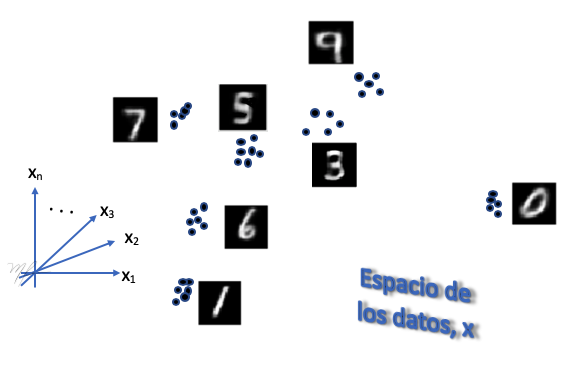
Considere el espacio n-dimensional de los datos como el ilustrado en la siguiente figura. Donde cada punto representan un datos (imágen de dígito). En el espacio original, los datos se agrupan en clusters que corresponden a un mismo dígito.

espacio datos

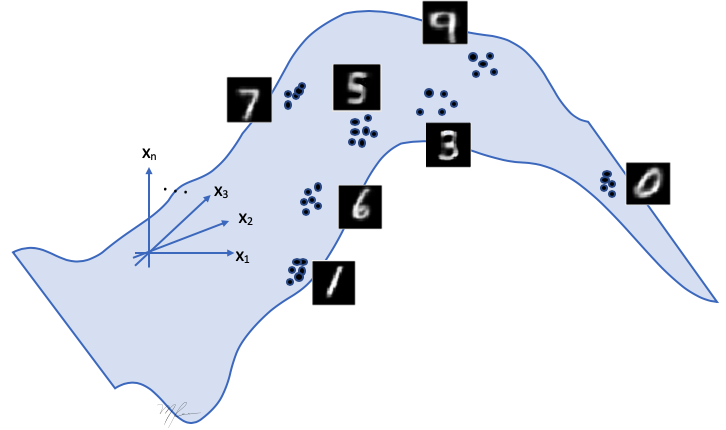
Luego, es posible pasar una función suave $%f$ de menor dimensión por dichos datos. Dicha $f$ es función del vector $z$ , llamado variable latente que tienen la información de que dígito generar (clase, inclinación, tamaño, grueso del trazo, etc.) y otros parámetros $\theta$ que especifican como pasar la definición dada por $z$ a valores de pixel.

(10)
$x_i = f(z_i; \theta)$

función_f

Como en el caso de Análisis de Componentes Principales (Principal Componente Analysis, PCA), tal vez sea necesario admitir una pequeña pérdida para proyectar los datos a la superficie $f$ . Generalmente, los clusters tienen funciones de densidades de probabilidad (Probability Density Functions, PDF) complejas y lo serán también sus proyecciones sobre la superficie de $f$ : multimodales, asimétricas, con huecos, colas pesadas, etc.

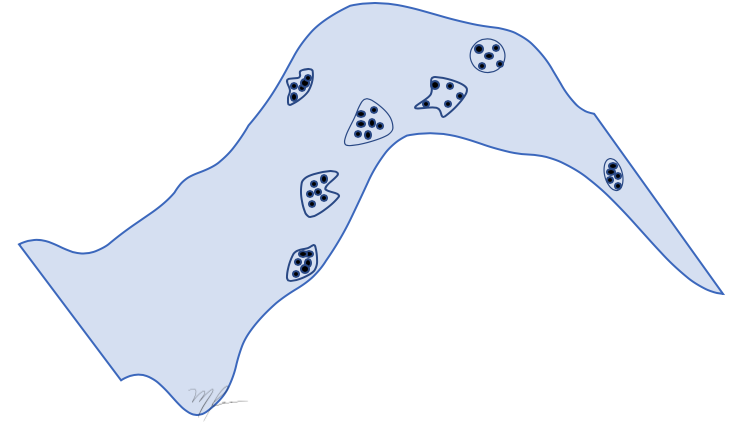
pdf datos

La clave de los VAE es que la PDF de las variables latentes $z$ ( $P(Z)$ ) de la función $f$ es mucho mas simple que la PDF de los datos $x$ ( $P(X)$ ). Esto se ilustra en la siguiente figura donde las PDFs de los datos (proyectadas sobre la superficie) son localmente tangentes a la superficie.

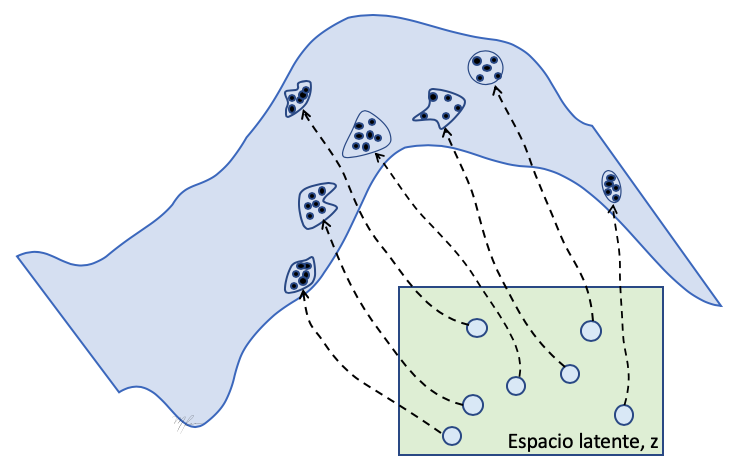
pdf latente

Como podemos ver, $f$ es un modelo generador de imágenes al que le introducimos $z$ , emplea $\theta$ y genera una imagen $x$ .

Gráficamente, el modelo generador se representa como en el siguiente diagrama

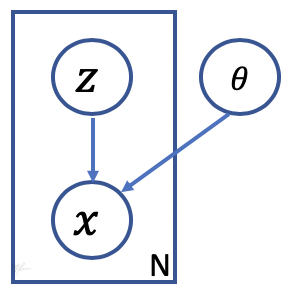
likelihood

donde las flechas indican la dependencia entre las variables y el rectángulo indica que podemos generar $N$ muestras de $x$ cambiando $z$ (muestreandola de acuerdo a $P(Z)$ ) con un solo conjunto de parámetros $\theta$ .

La siguiente figura ilustra el proceso de generación de imágenes $x$ .

pxz

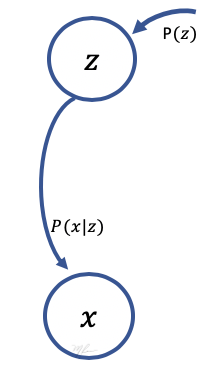
Se obtienen una instancia de la variable latente $z$ mediante el muestreo de $P(z)$ dada $z$ y $\theta$ (hemos omitido $\theta$ para efectos de simplificar la notación). A $P(x | z) \equiv P(x \, | \, z; \theta)$ se le denomina verosimilitud y se interpreta como que tan verosímil es observar la imagen $x$ para unos valores dados de $z$ y $\theta$ .

Si asumimos el error, pixel a pixel, entre la observación $x$ y la generada por el modelo $f$ sigue una distribución Gaussiana y que los errores son independientes (no hay correlación espacial), entonces la verosimilitud esta dada por

(11)
$P(x \, | \, z; \theta) = \frac{1}{\sqrt{2 \pi} \sigma^{n/2}} \exp \left( - \frac{1}{2 \sigma^2} \| x - f(z;\theta) \|^2\right)$

Notamos que pueden ser usadas otras distribuciones distintas de la Gaussiana. Por ejemplo, si los pixeles toman valores binarios ( $\{ 0,1\}$ ), entonces una distribución Bernoulli puede ser mas apropiada. Aunque es buen sabido la ventaja numérica que implica optimizar la log-verosimilitud que resulta ser cuadrática.

Otra forma de visualizar el proceso de generación es mediante la siguiente figura.

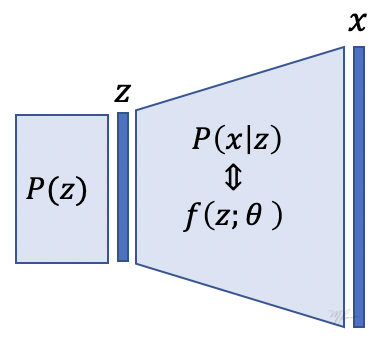
decoder

En ella se ilustra que $z$ se obtienen a partir (del muestreo) de $P(z)$ , luego la variable latente es empleada en el siguiente proceso para generar $x$ . Aqui podemos simplificar el proceso, hagamos la varianza (hiperparámetros del método) $\sigma$ en (11) muy pequeña tal que, dadas $z$ y $\theta$ la verosimilitud es una delta de Dirac y que el único valor posible para $x$ es:

$x = f(z; \theta)$
Esto simplifica el proceso, haciendo una parte completamente determinista, el mustreo de $P(z)$ sigue siendo el componente estocástico que permitirá generar variantes en $x$ .

Si consideramos un conjunto de observaciones $x_i$ y hacemos $z_i=y_i$ ( $z$ sólo codifica la clase del dígito), podemos aprender $\theta$ mediante un enfoque de máxima verosimilitud:

(13)
$\theta^\ast = \underset{\theta} {\arg \min} \prod_i P(x_i | z_i ; \theta)$

dicha optimización no es, en principio, complicada dada la dependencia continua de la verosimilitud en $\theta$ . Decimos “en principio” porque dependerá de la forma precisa de $f$ . Pero usando descenso estocástico se garantiza convergencia al menos a un mínimo local.

Ahora, para relacionar nuestro modelo generador $f$ con $P(X)$ hacemos explícita la dependencia en $z$ :

(12)
$\boxed{ P(x) = \int P(x \, | \, z; \theta) P(z) \, dz }$

Otra forma de escribir (12) es

(13)
$P(x) = E_{z \sim P(z)} \{ P(x| z)\}$
donde $z \sim P(z)$ (esto significa que $z$ se distribuye de acuerdo a $P(z)$ ).

Función Objetivo (Cota Bayesiana Variacional)

Los Autocodificadores Variacionales, VAEs, son un método para maximizar (12) en forma aproximada, proponiendo una forma simple para $P(z)$ y usando retropropagación.

Los dos puntos importantes en VAEs son:

No se especifica como la información es codificada en la variable latente $z$ . Esto es, no es necesario decir que información se codifica en que dimensión, no es necesario preocuparnos por dependencias; Las VAEs incrustarán la información en forma adecuada.
Aproxima la integral en (12) en forma eficiente. Evita integrar sobre todas las imágenes posibles $x$ (lo que es impráctico), de las cuales, para muchas la verosimilitud será prácticamente cero. En vez de ello, considera solo los ejemplos positivos, es decir integrará sobre $z$ 's tal que $P(x | z) >> 0$ .

De aquí y en lo sucesivo, hemos obviado la dependencia en $\theta$ de la verosimilitud: $P(x|z) \equiv P(x|z; \theta)$ .

Veamos una forma de generar $z$ a partir de una distribución; la idea es la siguiente:

En vez usar $P(z)$ para generar la variable latente $z$ usaremos una distribución approximada $Q(z | x) \approx P(z|x)$ . Si bien, $P(z)$ es la distribución de los valores latentes, la condicional $P(z|x)$ también debe corresponder a la misma distribución cuando usamos los datos $x$ ; y esta es su ventaja, nos permite hacer que $z$ dependa de $x$ . Entonces es de esperar que para $x$ 's similares tengamos $z$ 's similares. Como dijimos, usaremos $Q(z|x)$ que debe aproximar muy bien a $P(z|x)$ . Este paso require de ser estocástico. Es decir, cada vez que presentemos una imágen $x$ se genera una instancia de $z$ ; si presentamos varias veces un mismo dato $x_i$ , se generará una $z_i$ distinta.
Luego, dada $z$ generamos una aproximación de $x$ denotada por $\tilde x$ mediante $P(x | z)$ . Este paso se implementa totalmente determinista ( $\tilde x = f(z;\theta$ ).

En la siguiente figura se muestra el proceso de dos pasos de generacion de imágenes.

vae1

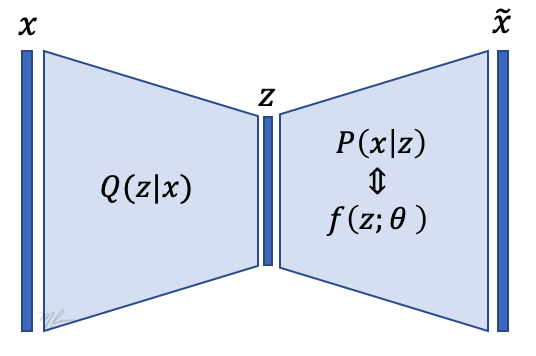
La dependencia entre las variables se muestran en la siguiente gráfica, en ella se muestra a la aproximación $Q(z|x)$ de $P(z|x)$ .

pzx

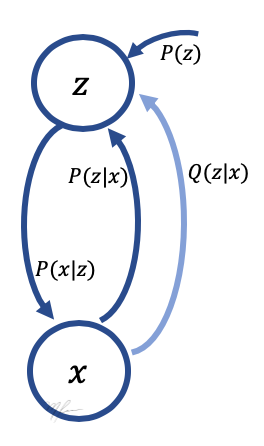
Para medir la diferencia entre nuestra aproximación $Q(z |x )$ y $P(z | x)$
usamos la Divergencia de Kullback-Leibler:

(14)
$D[Q(z|x) \|P(z|x)] = \sum_z Q(z | x) \log \frac{Q(z | x)}{P(z|x)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = E_{z \sim Q}\{\log Q(z | x) - \log P(z|x)\}$

Usando la regla de Bayes,

$P(z|x) = P(x \,| \, z) P(z) / P(x)$ ,
$\log P(z\,|\,x) = \log P(x\,| \, z) + \log P(z) -\log P(x)$ ,
y notando que $P(x)$ es independiente de $z$ ;

rescribimos (14):

(15)
$D[Q(z | x) \|P(z\,|\,x)] = E_{z \sim Q}\{ \log Q(z | x) - \log P(x\,|\,z) - \log P(z) \} + \log P(x)$

Notamos que $E_{z \sim Q}\{\log Q(z | x) - \log P(z)] = D[Q(z) \| P(z)\}$ y re-ordenando términos de (15):

(16)
$\boxed{\log P(x) - D[Q(z | x) \| P(z|x)] = \underbrace{E_{z \sim Q}\{ \log P(x\,|\,z) - D [Q(z | x) \| P(z) ] }_{\overset{def}{=}L} \} }$

Eq. (16) es importante porque el lado izquierdo contiene

El término que queremos maximizar: $P(x)$ (o $\log P(x)$ ).
Un término de error $D(Q(z | x) \| P(z|x))$ que se puede interpretar como una penalización es y es cero ssi $Q(z | x) = P(z|x)$ .

El lado derecho (definido como $L$ ) lado derecho es la forma computable y que puede ser optimizada mediante descenso de gradiente. A $L$ se le denomina la Cota Inferior Variacional (Variational Lower Bound) o Límite Inferior de la Evidencia (Evidence Lower Bound, ELBO). La ELBO es muy empleado en Métodos Bayesianos Variacionales muy útil para expresar problemas de inferecia estadística como problemas de optimización (Blei et al, 2017); es decir traducir problemas de inferir el valor de una variable a partir de otra a un problema de encontrar parámetros en funciones de costo (Ba et al., 2014), (Mnih et al., 2014), (Xu et al., 2015).

Optimización de la Cota Bayesiana Variacional de los VAE

Regresando al lado izquierdo de (16), lo que notamos es que si nuestra aproximación $Q$ es suficientemente buena, entonces maximizar la Cota Inferior Variacional equivale a maximizar $\log P(x)$ y por ende $P(x)$ . Esta maximización se hace con respecto a los parámetros de todo el sistema; parámetros que hemos obviado escribir, $\theta_q$ en $Q(z | x ; \theta_q)$ y $\theta$ en $P(x|z; \theta)$ (o lo que es lo mismo, en $f(z; \theta)$ .

Los puntos pendientes son

¿Cómo definir a $f(z;\theta)$ para que pueda mapear las variables latentes $z$ a imágenes $x$ ? La respuesta es usando un aproximador universal, es decir una red neuronal profunda (DNN). En dicho caso $\theta$ son los pesos de la DNN que pueden ser aprendidos mediante backpropagation si contamos con pares $(x,z)$ .
¿Cómo definir $Q(z| x)$ para que sea los suficientemente general y pueda representar a $P(z|x)$ ? La respuesta de nuevo es usando una DNN. Solo que ahora requerimos dos ingredientes. a) Darle una forma a $P(z)$ y b) introducir una componente estocástica para que la salida de la DNN (respuesta) a una misma $x$ variable de acuerdo a $P(z)$ .

El primer punto es realmente simple, se define una DNN que mapee del espacio latente al de las imágenes. Ver la siguiente figura

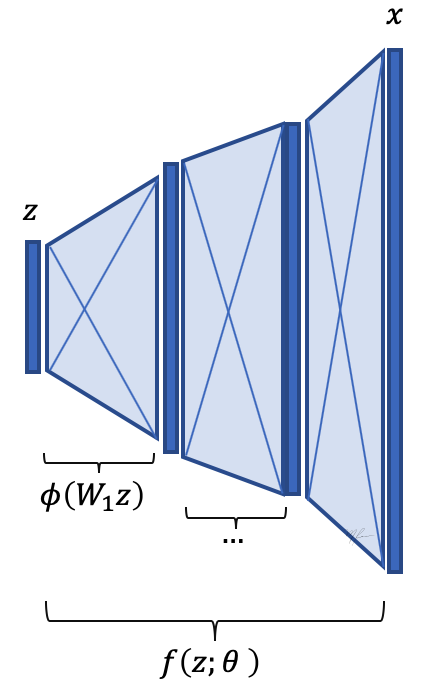
decoderDNN

El segundo punto es un poco mas complicado. Primero definimos $P(z)$ , la distribución de las variables latentes. Aprovechamos el hecho de que dada una variable aleatoria, digamos $z$ , con una cierta distribución, es posible crear otra variable aleatoria mediante una función determinística, denotada por $x=g(z)$ , con distribución muy distinta. Ver el código y gráficas siguientes.

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
m = 100

z = np.random.normal(loc=0., scale=1, size=(m,2))
x = z + z/np.abs(z)

plt.figure(figsize=(14,7))
plt.subplot(121)
plt.scatter(z[:,0], z[:,1], c='b')
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.title('z')
plt.subplot(122)
plt.scatter(x[:,0], x[:,1], c='r')
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.title('x')
plt.show()

png

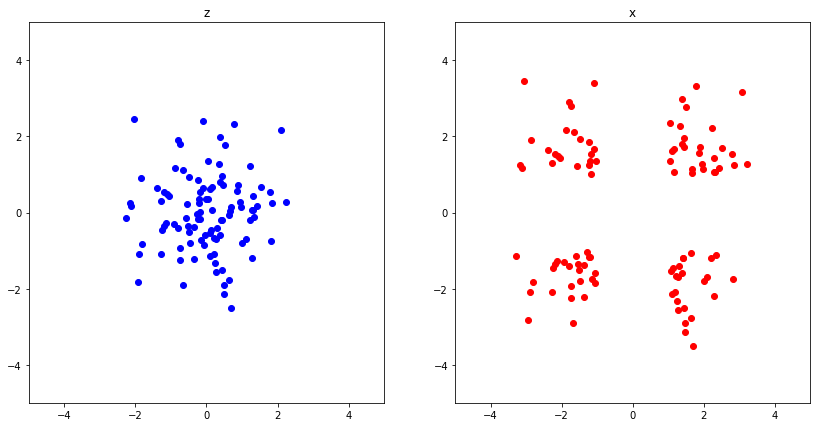
Entonces, proponemos que $P(z)$ sean una distribución Gaussiana multivariada,

(17)
$P(z) = \mathcal{N}(0, I),$

con media cero y varianza unitaria no correlacionada.

Luego, dado que elegimos generar $z$ a partir de los datos $x$ , esta debe ser también Gaussiana y proponemos:

(18)
$Q(z | x) = \mathcal{N}(\mu(x), \Sigma(x))$

donde $\mu(x)$ es el vector de medias y $\Sigma(x)$ la matrix de covarianza. Las distribuciones $P(z)$ , Gaussiana multivariada homogénea, y $Q(z|x)$ , Gaussiana multivariada no correlacionada, se ilustran en la siguiente figura.

p_q

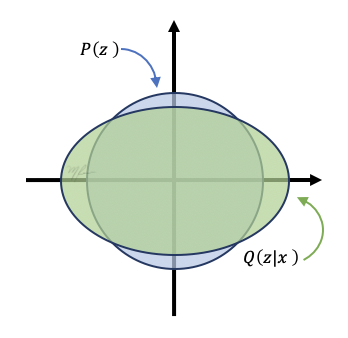
Dado que Divergencia KL entre dos Gaussianas de dimensión $n$ se define por:

(19)
$D[\mathcal{N}(\mu_0, \Sigma_0) \| \mathcal{N}(\mu_1, \Sigma_1)]= \frac{1}{2} \left[ \mathrm{tr}\,( \Sigma_1^{-1} \Sigma_0) + (\mu_1-\mu_0)^\top \Sigma_1^{-1} (\mu_1-\mu_0) - n + \log \left(\frac{\mathrm{det}\, \Sigma_1} {\mathrm{det}\, \Sigma_0} \right) \right]$

entonces, en nuestro caso se simplifica a

(20)
$D[\mathcal{N}(Q(z|x) \| P(z)] = D[\mathcal{N}(\mu(x) \| \Sigma(x)), \mathcal{N}(0, I)] \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \frac{1}{2} \left[ \mathrm{tr}\, \Sigma(x) + \mu(x)^\top \mu(x) - n - \log \mathrm{det}\, \Sigma(x) \right]$

Mas aun, si asumimos que $Q(z \, | \, x) = \mathcal{N}(\mu(x),\sigma^2(x) \, I)$ , con
$\mu (x) = [\mu_1(x), \mu_2(x), \ldots, \mu_n(x)]^\top \;\;\; \text{y} \;\;\; \sigma^2(x) = [\sigma^2_1(x), \sigma^2_2(x), \ldots, \sigma^2_n(x)]^\top$
podemos simplificar aun más la KL:

(21)
$\boxed{ D[\mathcal{N}(\mu(x), \sigma(x) I) \| \mathcal{N}(0, I)] = \frac{1}{2} \sum_i \left[ \sigma^2_i(x) + \mu_i(x)^2 - 1 - \log \sigma^2_i(x) \right] }$

La eq. (20) corresponde al segundo término del lado derecho de la función objetivo ELBO ( $L$ ). Para optimizar, uno requiere de estimar el gradiente también del primer término de la ELBO ( $L$ ). Para calcular un gradiente numérico uno tendía que usar cada dato $x$ en la base de datos $X$ y generar $z$ mediante $Q(z|x)$ . Luego con $P(x| z)$ una generar $\hat x$ , la cual tendrá un error respecto a la verdadera $x$ . Este error se puede usar mediante retropropagación (backpropagation) para tener gradiente de

$E_{z \sim Q} \{ P( x | z ) \}$

En vez de usar toda la base de datos, es mejor aun, usar un subconjunto de datos $x$ 's en la base de datos $X$ , obtener un estimado del gradiente para ser usado mediante gradiente estocástico.

Truco de reparametrización

Aun queda una cuestión, ¿cómo hacer que la DNN que implemente $Q(z|x)$ sea estocástica, es decir que si se evalua múltiples veces en un mismo dato $x_k$ se generen diferentes instancias $z_k \sim P(z)$ ? Pues las DNN tienen capas determinísticas, ante una misma $x$ generará una misma $z$ .

Primero, notamos que si

$y \sim \mathcal{N}(\mu, \sigma I)$
también se puede generar mediante

$y = \mu + \sigma \, \epsilon, \,\,\, \text{donde} \,\,\, \epsilon \sim \mathcal{N}(0, I)$

import numpy as np
import matplotlib.pyplot as plt

m   = 10000
mu  = 50
dev = 10.
y1      = np.random.normal(loc=mu, scale=dev*2, size=m)
epsilon = np.random.normal(loc=0, scale=1., size=m)
y2 = mu+dev*2*epsilon

plt.figure(figsize=(15,5))
plt.subplot(121)
_=plt.hist(y1, bins=30)
plt.title('$\mathcal{N}(\mu,\sigma^2)$')
plt.subplot(122)
_=plt.hist(y2, bins=30)
_=plt.title('$\mu + \sigma^2 \, \epsilon,$ con $\epsilon \sim \mathcal{N}(0,1)$')

png

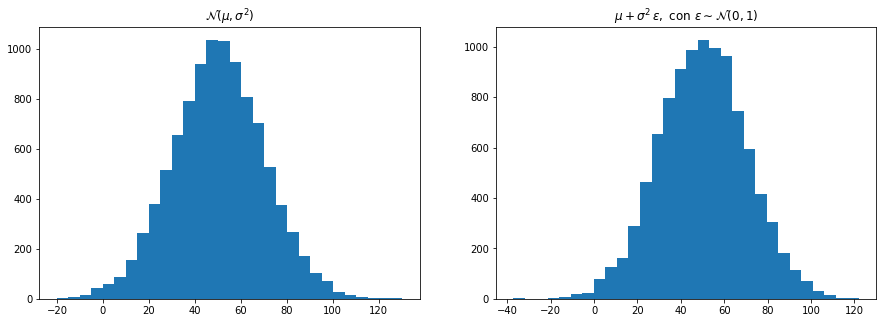
Poniendo todo junto, el Autoencoder Variacional se representa mediante la siguiente figura.

vae2

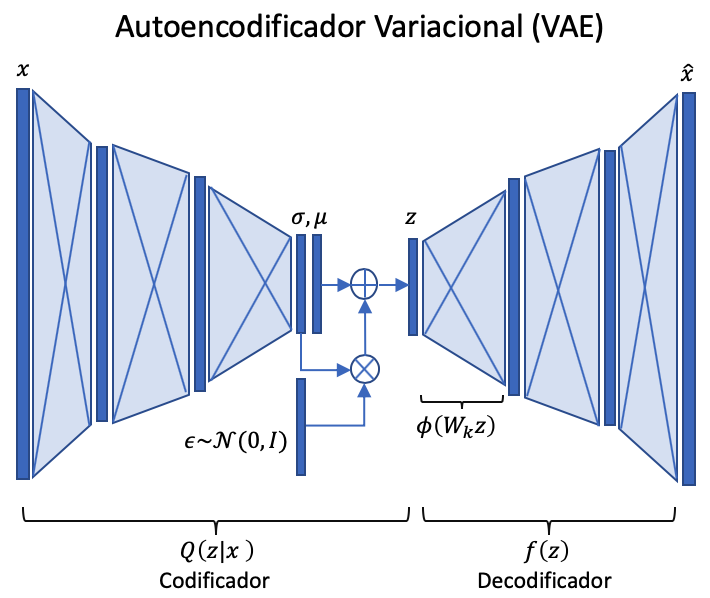
En la figura de arriba se aprecia que $Q(x | z)$ “codifica” $x$ en $z$ y $f(z)$ “decodifica” $z$ en $\hat x$ . También se parecia como $\mu(x)$ y $\sigma(x)$ se obtienen mediante una DNN determinística y que $z$ se obtiene mediate el "truco de la reparametrización. Cuando la red se entrena en forma completa, tanto el propagación hacia adelante como la retropopagación (para calcular el gradiente) se hace a través de capas (layers) determinísticas y continuas sobre los parámetros de $Q(z|x)$ , $P(z)$ y $f(x)$ . Por lo anterior, las distribuciones $Q(z|x)$ y $P(z)$ denben ser necesariamnete continuas (no se aceptan distribuciones dicontinuas).

Probando con la BD Dígitos de MNIST

Usaremos como ejercicio para implemnetar un VAE el reproducir imágenes correspondientes a dígitos manustritos de la base de datos MNIST (LeCun et al., 1998)

from keras.layers import Input, Dense, Lambda
from keras.models import Model
from keras import backend as K
from keras import objectives
from keras.datasets import mnist
import numpy as np

Using TensorFlow backend.

Lectura de datos

(x_train, y_train), (x_test, y_test) = mnist.load_data()
 
x_train = x_train.astype('float32') / 255.
x_test  = x_test.astype( 'float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test  = x_test.reshape( (len(x_test),  np.prod(x_test.shape[1:])))

x_train.shape

(60000, 784)

Definición de variables

epochs       = 5        # número de epocas
batch_size   = 100      # tamaño del lote
original_dim = x_train.shape[1]    # 784 tamaño de las imágenes MNIST
intermediate_dim = 256  # dimensión intermedia
latent_dim   = 2        # número de parámetros del espacio latente

Función de muestreo del espacio latente

def sample_z(args):
    mu, log_sigma2 = args
    epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.)
    return mu + K.exp(log_sigma2 / 2) * epsilon

Codificador (encoder)

Usamos la APi de Keras porque el Codificador (encoder) requiere de dos salidas: media y log-varianza.

# capa de entrada (datos) al decodificador
encoderIn = Input(shape=(original_dim,), 
                  name="input")
# capa intermendia
encoder_H1 = Dense(units=intermediate_dim, 
                   activation='relu', 
                   name="encoding")(encoderIn)
# media y log-varianza del espacio latente
z_mu         = Dense(units=latent_dim, 
                   name="mean")(encoder_H1)
z_log_sigma2 = Dense(units=latent_dim, 
                   name="log-variance")(encoder_H1)
# muestreo de z con el truco de la reparametrizacion
z          = Lambda(sample_z, 
                    output_shape=(latent_dim,))([z_mu, z_log_sigma2])

# Modelo del "encoder" las salidas son: media, log-varianza y muestra
encoder = Model(inputs=encoderIn, 
                outputs=[z_mu, z_log_sigma2, z],
                name="encoder")

encoder.summary()

__________________________________________________________________________________________________
Layer (type)                    Output Shape         Param #     Connected to                     
==================================================================================================
input (InputLayer)              (None, 784)          0                                            
__________________________________________________________________________________________________
encoding (Dense)                (None, 256)          200960      input[0][0]                      
__________________________________________________________________________________________________
mean (Dense)                    (None, 2)            514         encoding[0][0]                   
__________________________________________________________________________________________________
log-variance (Dense)            (None, 2)            514         encoding[0][0]                   
__________________________________________________________________________________________________
lambda_1 (Lambda)               (None, 2)            0           mean[0][0]                       
                                                                 log-variance[0][0]               
==================================================================================================
Total params: 201,988
Trainable params: 201,988
Non-trainable params: 0
__________________________________________________________________________________________________

Una vez que tenemos la media y la log-varianzas generamos la muestra para enviarla al decodificador.

Esta operación la implementamos mediante una capa especial de Keras, la capa Lambda (que nos recuerda las funciones lambda de python).

   keras.layers.Lambda(function, 
                       output_shape=None, 
                       mask        =None, 
                       arguments   =None)

Parámetros

function: la función a evaluar

output_shape: forma del tensor de salida (relevante en Theano)

input: forma de la salida

arguments: Diccionario de argumentos de la función a evaluar

La implementación de la función de muestreo es

def sample_z(args):
    z_mu, z_log_sigma2 = args
    epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.)
    return z_mu + K.exp(z_log_sigma2 / 2) * epsilon

Visualización del Codificador

### Visualización del Codificador

from keras.utils import plot_model
plot_model(encoder, to_file='model_encoder.png',show_shapes=True, show_layer_names=True)

Encoder

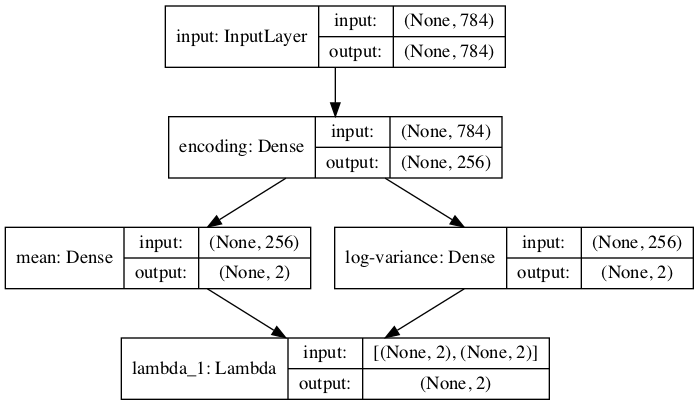
model_plot

Decodificador (decoder)

# capa de entrada (datos) al decodificador
decoderIn  = Input(shape=(latent_dim,), 
                   name="decoder_input")
# capa intermedia
decoder_H1 = Dense(intermediate_dim, 
                   activation='relu',    
                   name="decoder_h")(decoderIn)
# capa de salida con dimensiones igual a las orginales
decoderOut = Dense(original_dim,     
                   activation='sigmoid', 
                   name="flat_decoded")(decoder_H1)
# definición del modelo del decodificador
decoder    = Model(inputs=decoderIn, 
                   outputs=decoderOut, 
                   name="decoder")

decoder.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
decoder_input (InputLayer)   (None, 2)                 0         
_________________________________________________________________
decoder_h (Dense)            (None, 256)               768       
_________________________________________________________________
flat_decoded (Dense)         (None, 784)               201488    
=================================================================
Total params: 202,256
Trainable params: 202,256
Non-trainable params: 0
_________________________________________________________________

Vizualización del Decodificador

### Vizualización del Decodificador

plot_model(decoder, to_file='model_decoder.png',show_shapes=True, show_layer_names=True)

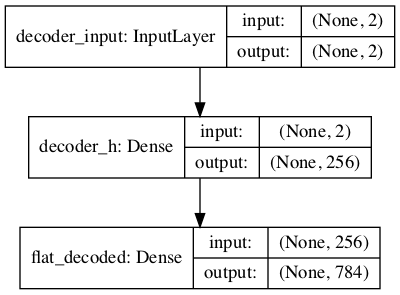
model_plot

VAE: Encoder + Decoder

Combinamos el codificador y el decodificador en un solo modelo.

$z = \phi_C(x)$
representa el codificador

$\tilde x = \phi_D(z)$
el decodificador. Entonces, hacemos la composición

$\tilde x = \phi_D( \phi_C(x))$

vaeOut = decoder(encoder(encoderIn)[2])
# construimos el  modelo
vae = Model(inputs=encoderIn, outputs=vaeOut)
vae.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input (InputLayer)           (None, 784)               0         
_________________________________________________________________
encoder (Model)              [(None, 2), (None, 2), (N 201988    
_________________________________________________________________
decoder (Model)              (None, 784)               202256    
=================================================================
Total params: 404,244
Trainable params: 404,244
Non-trainable params: 0
_________________________________________________________________

Visualización del VAE

plot_model(vae, to_file='model_vae.png',show_shapes=True, show_layer_names=True)

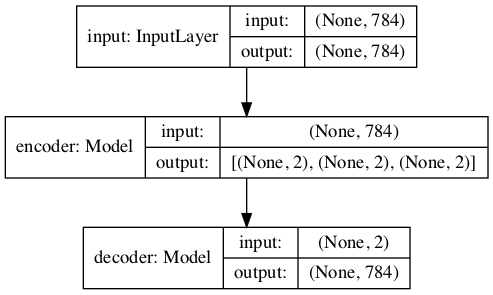
model_plot

Función de pérdida para el VAE (ELBO)

Como vimos en la derivación, la función de pérdida usada en autoncoders variacionales es la ELBO (16), una combinación de la entropía cruzada binaria $\log P(x|z)$ y la Divergencia de Kullback–Leibler $D [ Q(z|x) \| P(z) ]$ en (21).

def ELBO(x, x_decoded_mean):
    # log P(x|z)
    logP = original_dim * objectives.binary_crossentropy(x, x_decoded_mean)
    # D(Q(z|x)||P(z))
    Dkl =  0.05 * K.sum(K.exp(z_log_sigma2) + K.square(z_mu) - 1. -  z_log_sigma2 , axis=-1)
    return logP + Dkl
 
vae.compile(optimizer='rmsprop', loss=ELBO, metrics=['accuracy'])

Ajuste del Modelo,

vae.fit(x_train, x_train,
              shuffle    = True,
              epochs     = epochs,
              batch_size = batch_size,
              validation_data=(x_test, x_test),
              verbose=2)

Train on 60000 samples, validate on 10000 samples
Epoch 1/5
 - 2s - loss: 155.7120 - acc: 0.0127 - val_loss: 155.4324 - val_acc: 0.0120
Epoch 2/5
 - 2s - loss: 154.9287 - acc: 0.0132 - val_loss: 154.8914 - val_acc: 0.0095
Epoch 3/5
 - 2s - loss: 154.2709 - acc: 0.0125 - val_loss: 154.4437 - val_acc: 0.0111
Epoch 4/5
 - 2s - loss: 153.7247 - acc: 0.0121 - val_loss: 153.8589 - val_acc: 0.0109
Epoch 5/5
 - 2s - loss: 153.2183 - acc: 0.0123 - val_loss: 153.5299 - val_acc: 0.0145

<keras.callbacks.History at 0x7f60b7690c88>

Probando el Generador (decodificador)

numImgs = 30
newrows,newcols=28,28
lo, hi  = -3.,3.

z1 = np.linspace(lo, hi, numImgs)
z2 = np.linspace(lo, hi, numImgs)

import matplotlib.pyplot as plt

plt.figure(figsize=(15,15*newcols/newrows))
canvas=np.zeros((newrows*numImgs,newcols*numImgs))
for i in range(numImgs):
    for j in range(numImgs):
        z=np.array([z1[i], z2[j] ])
        z=np.expand_dims(z, axis=0)
        Im=decoder.predict(z)
        canvas[newrows*i:newrows*(i+1), newcols*j:newcols*(j+1)] = Im.reshape((newrows,newcols))
        
plt.imshow(canvas, 'gray')
plt.axis('off')        
plt.show()

png

Despliege del espacio latente generados por los datos, las etiquetas de los dígitos se usan para colorear cada $z$ .

x_test_encoded = encoder.predict(x_test, batch_size=batch_size)[0]
plt.figure(figsize=(12, 10))
plt.scatter(x_test_encoded[:,0], x_test_encoded[:,1], c=y_test, cmap='jet') 
plt.colorbar()
plt.show()

png

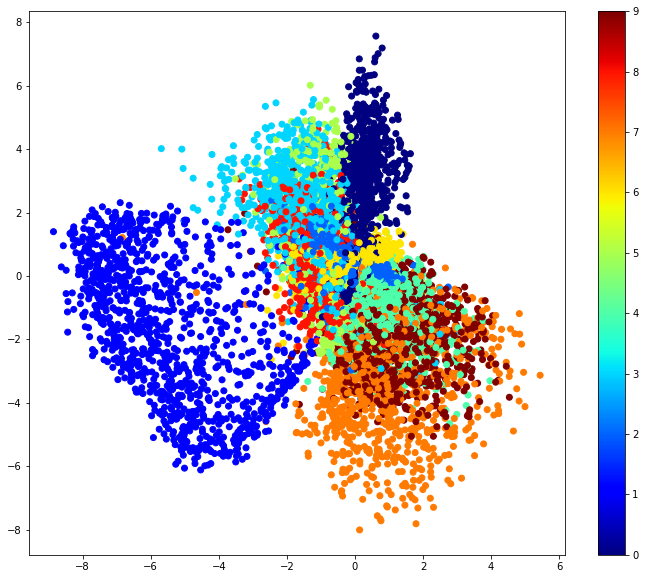
Referencias

(Lagr and Bok, 2019) Jakub Langr and Vladimir Bok, GANs in Action: Deep learning with Generative Adversarial Networks, Meanning Pub, 2019.

(Kingma and Welling, 2014) Diederik P Kingma and Max Welling. Auto-encoding variational Bayes.
ICLR, 2014.

(Jimenez-Rezende et al, 2014) Danilo Jimenez Rezende, Shakir Mohamed, and Daan Wierstra. Stochastic backpropagation and approximate inference in deep generative mod- els. In ICML, 2014.

(Sohn et al, 2015) Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning structured output representation using deep conditional generative models. In NIPS, 2015.

(Dorech, 2016) Doersch, C. 2016. Tutorial on Variational Autoencoders. arXiv e-prints arXiv:1606.05908.

(Blog de Altosaar) Jann Altosaar’s Blog, Tutorial - What is a variational autoencoder?

(Blei et al, 2017) D. M. Blei and A. Kucukelbir and J. D. McAuliffe, Variational Inference: A Review for Statisticians, Journal of the American Statistical Association 112 859-877 (2017)

(Ba et al., 2014) J. Ba, V. Mnih, and K. Kavukcuoglu. Multiple object recognition with visual attention. arXiv preprint arXiv:1412.7755, 2014.

(Mnih et al., 2014) V. Mnih, N. Heess, A. Graves, et al. Recurrent models of visual attention. in Proc. NIPS, pp 2204–2212, 2014.

(Xu et al., 2015) K. Xu, J. Ba, R. Kiros, K. Cho, A. C. Courville, R. Salakhutdinov, R. S. Zemel, and Y. Bengio. Show, attend and tell: Neural image caption generation with visual attention. In Proc. ICML, vol 14, pp 77–81, 2015.

(LeCun et al., 1998) Y. LeCun, L. Bottou,Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition.
Proceedings of the IEEE, 86(11):2278–2324, 1998.