La UNet

Version 0.1

Mariano Rivera

mayo 2019

¿Que aprenderemos?

  1. Inspiradoes en los autoencodificadores: una red que dada una imagen de entrada produce una imagen de salida.
  2. Segmentaremos imágenes.
  3. Capa de concatenacion.
  4. Capa Lambda.
  5. Capa UpSampling.
  6. Usaremos la API de Keras exhastivamente.

Autocodificadores (Antoencoders)

Seminales aplicaciones de la arquitectura de autocodificadores fueron:

Un autocodificador es una red que se puede representar mediante el esquema siguiente.

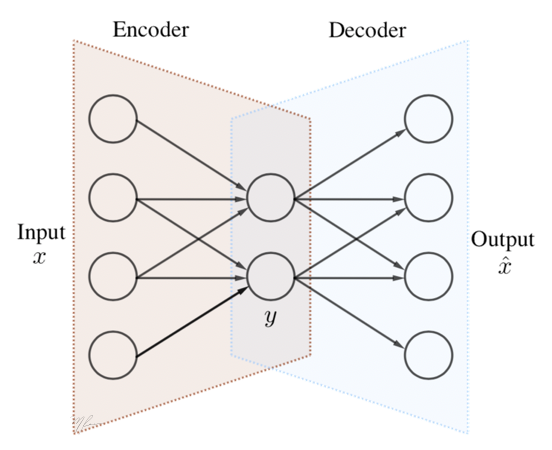
autoencoder

La primera motivación de los autocodificadores es tomar vector de entrada x∈Rnx \in \mathbb{R}^{n} para entrenar el sistema tal que la salida x^\hat x sea lo mas parecido a la entrada. La cuestión es que como paso intermedio, la red secuencial es obligada a producir un vector de menor dimención y∈py \in \mathbb{p}, con p<np<n. Si esto es logrado, el entrenamiento de la red permite hacer una reconstrucción fidedigna de la entrada, la red puede separarse en dos etapas. Un codificador que mapea los datos de entrada xx a los datos codificados (comprimidos) yy, y=E{x}y = \mathcal{E}\{x\}, un decodificador que permite restaurar los datos a partir de su versión codificada (comprimida), x^=D{y}\hat x = \mathcal{D}\{y\}.

Matemáticamente esto lo expresamos como sigue. Asumamos en coordenadas homogéneas a x∈Rnx \in \mathbb{R}^n, el autocodificador esta dado por

(1)
y=ϕ(Wex) y = \phi(W_e x)

y el decodificador por

(2)
x^=ϕ(Wdy) \hat x = \phi(W_d y)

con y∈Rpy \in \mathbb{R}^p tal que p<np<n. Luego, la forma de entrenar el autoencodificador es mediante la solución del siguiente problema de optimización

(3)
arg⁡min⁡We,Wd∥x−x^∥=∥x−ϕd(Wdy)∥=∥x−ϕd(Wd ϕd(Wex))∥ \underset{W_e, W_d}{ \arg \min} \| x - \hat x\| = \| x - \phi_d( W_d y) \| = \|x -\phi_d(W_d \, \phi_d( W_e x))\|

Autoencoders y PCA

Note que si el sistema es lienal, eliminamos las no-linealidades al hacer las funciones de activación son lineales, tenemos que en codificador esta dado por

(4)
y=Wex y = W_e x

y el decodificador

(5)
x^=Wsy \hat x = W_s y

la función objetivo será de la forma

(6)
arg⁡min⁡We,Wd∥x−x^∥=∥x−WdWex∥ \underset{W_e, W_d}{ \arg \min} \| x - \hat x\| = \|x - W_d W_e x\|

Entonces (4) es la proyección de x en los vectores renglón de WeW_e y la decodificación se obtienen al proyectar la variable codificada yy sobre los vectores renglón de WdW_d, para tener recostrucción perfecta deberemos tener WdWe=IW_d W_e = I.

En el caso de PCA, y=U⊤xy= U^\top x y x^=Uy\hat x = U y donde U es una matriz unitaria (UU⊤=U⊤U=IU U^\top = U^\top U = I), restricción que en (6) no aparece, pero el espacio expandido por WeW_e será el mismo que por U⊤U^\top.

Introducción de la Unet

Considremos el siguiete esquema donde los bloques mostrados son del tipo convolucional, no nos preocupemos por los detalles por ahora. Este esquema nos recuerda un poco a las redes residuales, que a groso modo se basan en bloqes que implementan x=x+F(x)x = x + F(x). La primara cuestión que surge con el bloque ResNet es si la suma es la mejor forma de combinar el vector de entrada y el procesado (residual). la respuesta es que no lo sabemos, por lo que lo mejro seria dejar a que este forma de combinar ambos tensores sea aprendida por la red.

El nuevo esquema mostrado es una generalización al bloque ResNet. A este componete elemental de la Unet llamaremos Bloque-U e implementa la operación

(1)
x^=G([x∣F(x)]) \hat x = G([x | F(x)])
donde [  ∣ ][ \; | \, ] representa el operador de concatenación, GG es el mecanismo aprendido para combinar xx y F(x)F(x). Note que si F=∅F=\varnothing, el bloque se comporta como un simple convolucional x^=G(x)\hat x = G(x).

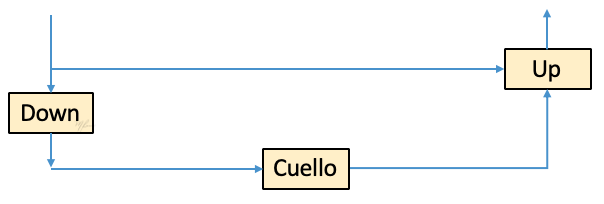
unet0

En este bloque pretenderemos que F(x)F(x) implemente un procesamiento sobre xx que implique la estimación de características de mayor complejidad (mas profundas) que las realizadas por GG, por ello el Bloque Down será convolucional: increementará los canales y decrementará las dimensiones espaciales de xx.

El Bloque Up, además de implementar la transformación GG, ajustará las dimensiones de los tensores de entrada para que sean concatenables.

El Bloque Cuello de Botella implementará un procesamiento extra que implicará estimar características mas profundas (mayor complejidad) en xx. Y es aquí donde ocurre la mayor diferencia con la ResNet, podemos implementar el cuello de botella como otro Bloque-U como se ilustra en la siguiente figura.

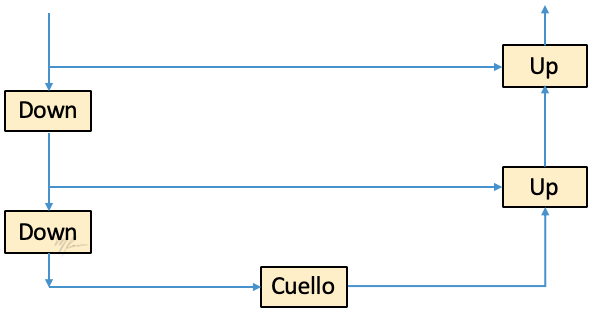
unet1

Que resulta en el el modelo matemático definido por

(2)
x^0=G1([x0∣G2([x1∣F(x)]) \hat x_0 = G_1 ( [ x_0| G_2 ([ x_1 | F(x) ])

Este construcción recursiva la podemos continuar en tanto la dimensiones espaciales de xx lo permitan. Luego en una siguiente recursión tendremos un esquema como el que a continuación se ilustra.

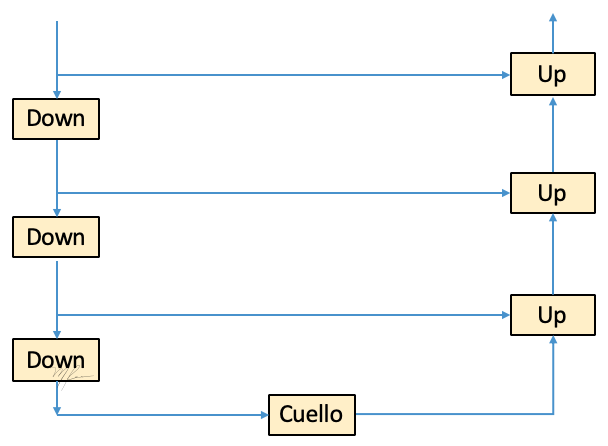
unet2

Este es el principio de la Unet propueta por Ronneberger et al. (2015), y se relaciona intimamente con los autoencodificadores en el sentido de que tenemos un tensor de entrada y uno de salida. Su arquitectura es muy similar, solo que ahora, tenemos ligas puente entre distintos niveles del autocodificador por lo que pretendemos tener una versión comprimida de los dato en alguna etapa intermedia; la red no es entendible como un sitema compuestompor un codificador y un decodificador, sino es un sistema completo.

En la siguiente figura se ilustra la arquitectura de la UNet que implementaremos.

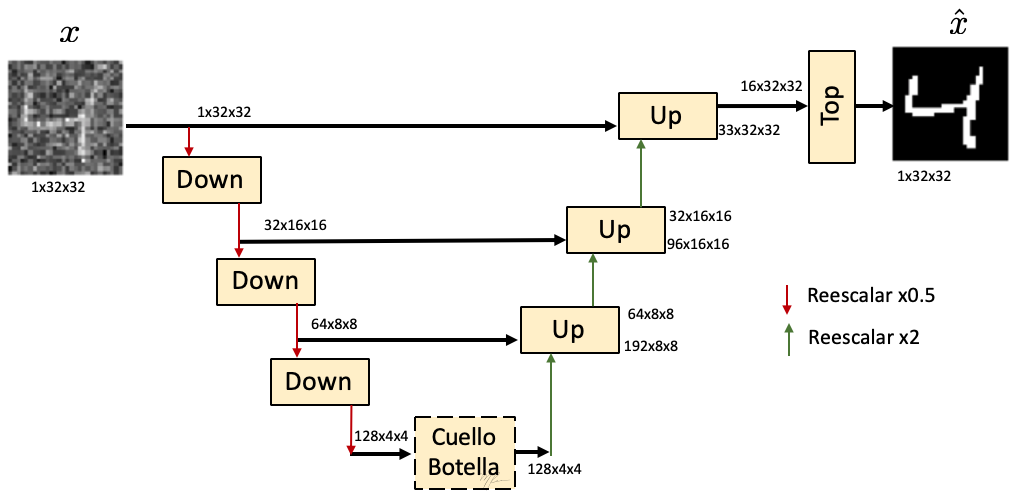
unet_esquema

La tarea a la que nos enfocaremos es la segmentación de imágenes (parches) ruidosas de dígitos. En el esquema anterior, las ligas indican el flujode datos y las dimensiones de los tensores se ulustran en el formato (num_canales, num_genglones, num_columnas). Notemos que conforme vamos a niveles mas profundos los tensores incrementan en número de canales y decrementan es dimensiones espaciales.

Regresando a la Unet que aquí implementamos, los bloques mas sencillos de definir son el cuello de botella (Neck), y la cabeza (Top). En la siguiente figura se muestra esquemáticamente los componentes de estos dos bloques convolucionales.

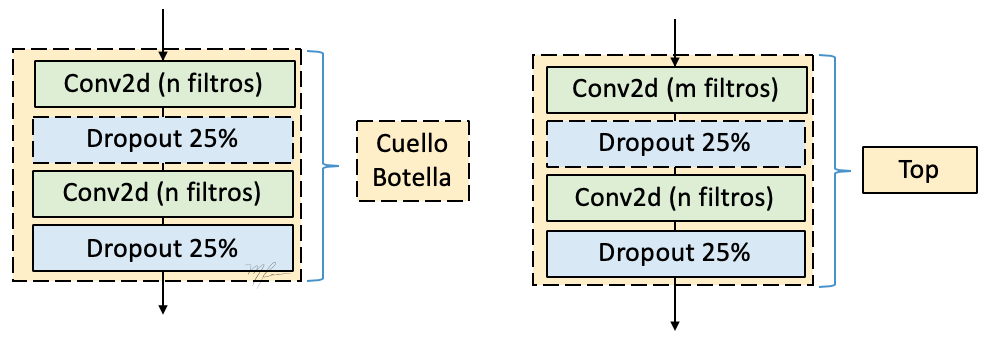
neck_top

Por otro lado los bloews Down y Up se componen de acuerdo al siguiente esquema:

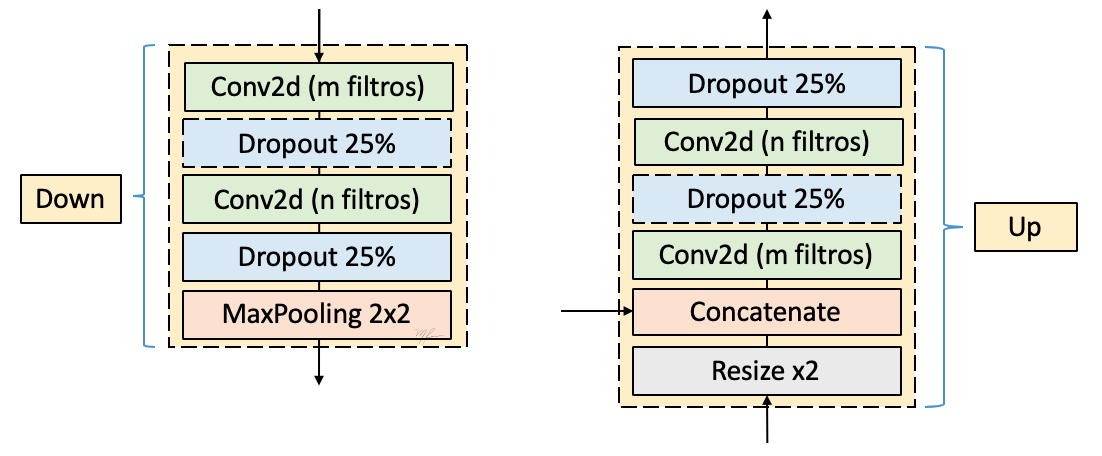
down_up

Entonces el Bloque Unet introducido al inicio de esta sección, se representa con mas detalles como en la siguiente figura.

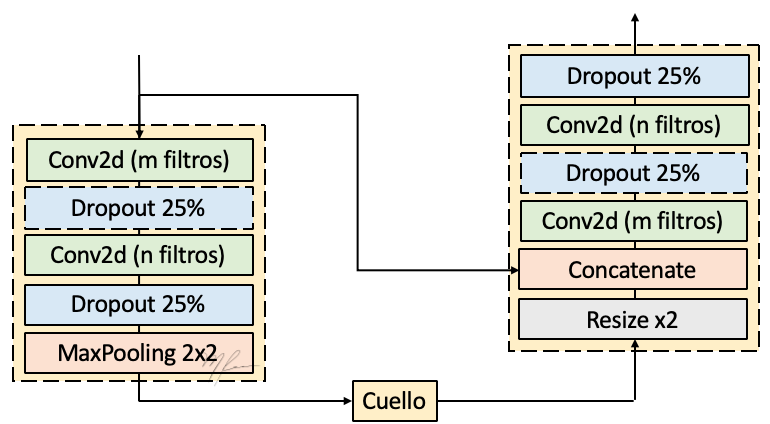
unet0_ext

Aunque la UNet fue concevida inicialmente para segmentación se han publicado variantes que implementan regresión imagen-imagen, ejemplos de ellos son

Bibliografía

Autoencoders

(Olshausen et al., 1996) Bruno A Olshausen, and David J Field. Emergence of simple-cell recep- tive field properties by learning a sparse code for natural images. Nature, 381(6583):607–609, 1996.

(Lee et al., 2006) Honglak Lee, Alexis Battle, Rajat Raina, and Andrew Y Ng. Efficient sparse coding algorithms. In NIPS, 2006.

(Vincent et al., 2008) Pascal Vincent, Hugo Larochelle, Yoshua Bengio, and Pierre-Antoine Manzagol. Extracting and composing robust features with denoising autoencoders. In ICML, 2008.

(Bengio et al., 2014) Yoshua Bengio, Eric Thibodeau-Laufer, Guillaume Alain, and Jason Yosinski. Deep generative stochastic networks trainable by backprop. ICML, 2014.

UNet

(Ronneberger et al., 2015) Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-Net: Convolutional Networks for Biomedical Image Segmentation. MICCAI (3) 2015: 234-241

(Dosovitskiy et al., 2015) P. Fischer, E.I. Philip Häusser, C. Hazirbas, V. Golkov, P. va der Smagt, D. Cremers, and T. Brox. FlowNet: Learning Optical Flow with Convolutional Networks," IEEE ICCV pp. 2758-2766 (2015).

(A. Reyes-Figueroa, 2019) Alan Reyes-Figueroa and Mariano Rivera. Deep neural network for fringe pattern filtering and normalisation, arXiv:1906.06224v1.

(Hu et al., 2019) X. Hu, M. A. Naiel, A Wong, M. Lamm and P, Fieguth. RUNet: A Robust UNet Architecture for Image Super-Resolution, CVPR (2019)

Implementación en Keras de la UNet

import os
os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID";
os.environ["CUDA_VISIBLE_DEVICES"]="1";  

import keras
from keras.layers import Input, Dense, Activation, Conv2D
from keras.layers import MaxPooling2D, Dropout, UpSampling2D
from keras.layers import BatchNormalization, Reshape
from keras.layers.merge import Concatenate
from keras.models import Model
from keras.models import Sequential
from keras.utils import plot_model

import numpy as np
import matplotlib.pyplot as plt

Using TensorFlow backend.

def resumen(model=None):
    '''
    Descipción del modelo en foam compacta (la prefiero a `summary` de keras)
    '''
    header = '{:4} {:16} {:24} {:24} {:10}'.format('#', 'Layer Name','Layer Input Shape','Layer Output Shape','Parameters'
    )
    print('='*(len(header)))
    print(header)
    print('='*(len(header)))
    count=0
    count_trainable=0
    for i, layer in enumerate(model.layers):
        count_trainable += layer.count_params() if layer.trainable else 0
        input_shape = '{}'.format(layer.input_shape)
        output_shape = '{}'.format(layer.output_shape)
        str = '{:<4d} {:16} {:24} {:24} {:10}'.format(i,layer.name, input_shape, output_shape, layer.count_params())
        print(str)
        count += layer.count_params()
    print('_'*(len(header)))
    print('Total Parameters : ', count)
    print('Total Trainable Parameters : ', count_trainable)
    print('Total No-Trainable Parameters : ', count-count_trainable)

Lectura de datos (Mnist)

El objetivo es segmentar imágenes con ruido de dígitos (28x28 pixeles) de la popular base de datos MNIST

from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

Cargar la base de datos MNIST que vienen con keras

from keras.datasets import mnist

# lectura de los datos
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

print('Dimensiones del conjunto de entrenamiento: ', train_images.shape)
print('Dimensiones del conjunto de evaluación: ',    test_images.shape)

num_data, nrows, ncols = train_images.shape

Dimensiones del conjunto de entrenamiento:  (60000, 28, 28)
Dimensiones del conjunto de evaluación:  (10000, 28, 28)

Datos: binarización y añadido de ruido

X_train = np.copy(train_images).astype('float64')/255.
Y_train = np.copy(train_images).astype('float64')/255.
X_test  = np.copy(test_images).astype('float64')/255.
Y_test  = np.copy(test_images).astype('float64')/255.

sigma = 0.4
X_train += np.random.normal(loc=0, scale=sigma, size=train_images.shape)
X_test  += np.random.normal(loc=0, scale=sigma, size=test_images.shape)
Y_train = Y_train>0.5
Y_test  = Y_test>0.5

num_test_images, num_rows, num_cols = X_test.shape
X_test.shape

(10000, 28, 28)

imgs=10
plt.figure(figsize=(14,4))
for i in range(imgs):
    plt.subplot(3,imgs,i+1)
    idx = list(train_labels).index(i)
    plt.imshow(train_images[idx], 'gray')
    plt.title(train_labels[idx])
    plt.axis('off')
    
    plt.subplot(3,imgs,i+1+imgs)
    idx = list(train_labels).index(i)
    plt.imshow(X_train[idx], 'gray')
    #plt.title(train_labels[idx])
    plt.axis('off')

    plt.subplot(3,imgs,i+1+2*imgs)
    idx = list(train_labels).index(i)
    plt.imshow(Y_train[idx], 'gray')
    #plt.title(train_labels[idx])
    plt.axis('off')

png

Se muestran, en el primer renglón ejemplos de cada dígito en la base de datos, en el segundo renglón los datos ruidosos usados como entrada y el el tercer renglón la salida binaria esperada.

X_train = np.expand_dims(X_train, axis=3)
Y_train = np.expand_dims(Y_train, axis=3)
X_test  = np.expand_dims(X_test,  axis=3)
Y_test  = np.expand_dims(Y_test,  axis=3)

print('Dimensiones de entradas (X) para entrenamiento  (imagenes x rows x cols) =', X_train.shape)
print('Dimensiones de saida (Y) para entrenamiento     (imagenes x rows x cols) =', Y_train.shape)
print('Dimensiones de entradas (X) para evaluación     (imagenes x rows x cols) =', X_test.shape)
print('Dimensiones de saida (Y) para evaluación        (imagenes x rows x cols) =', Y_test.shape)

Dimensiones de entradas (X) para entrenamiento  (imagenes x rows x cols) = (60000, 28, 28, 1)
Dimensiones de saida (Y) para entrenamiento     (imagenes x rows x cols) = (60000, 28, 28, 1)
Dimensiones de entradas (X) para evaluación     (imagenes x rows x cols) = (10000, 28, 28, 1)
Dimensiones de saida (Y) para evaluación        (imagenes x rows x cols) = (10000, 28, 28, 1)

Código del Modelo

from keras import models
from keras.layers import Conv2D, Dropout, MaxPooling2D, UpSampling2D, Concatenate
from keras import optimizers
from keras.backend import tf as tf
from keras.layers import Lambda, Input

La lista filters_per_block define el número de canales en cada etapa de la Unet, la profundidad de la Unet se adapta de acuerdo a la longitud de dicha lista.

_, num_rows, num_cols, num_channels = X_train.shape
img_dim          = (num_rows, num_cols, num_channels,)
filters_per_block = np.array([num_channels, 32, 64, 128])
num_blocks        = len(filters_per_block)   
kernel_size       = (3,3)
drop              = 0.25*np.ones(num_blocks)
drop

array([0.25, 0.25, 0.25, 0.25])

Encoder

Los bloques convolucionales Down tienen la estructura:

  1. Conv2D 3x3 con activación ReLu con padding para matener la dimensión espacial

  2. Conv2D 3x3 con activación ReLu con padding para matener la dimensión espacial

  3. Dropoout del 25% (parametro definible)

  4. MaxPolling 2x2 que reduce la dimensión espacial

No se usa Bloque Cuello de Botella.

nm= 'encoder'
Xdicc={}

Xin  = Input(shape=img_dim, name="x_true")

X = Lambda(lambda image: tf.image.resize_images(image, (32, 32)))(Xin)
# resize image layer
Xdicc[0] = X
numFilters=filters_per_block[0]
print(0, numFilters, X.shape)

for i in range(1,num_blocks):
    numFilters=filters_per_block[i]
    X = Conv2D(numFilters, kernel_size=kernel_size, padding='same', activation='relu', name='encoder-conv1'+str(i))(X) 
    X = Conv2D(numFilters, kernel_size=kernel_size, padding='same', activation='relu', name='encoder-conv2'+str(i))(X)
    X = Dropout(rate=drop[i], name='encoder-drop'+str(i))(X)
    X = MaxPooling2D(pool_size=(2,2), padding='valid', name='encoder-maxpool'+str(i))(X)
    Xdicc[i] = X
    print(i, numFilters, Xdicc[i].shape) 
      

0 1 (?, 32, 32, 1)
1 32 (?, 16, 16, 32)
2 64 (?, 8, 8, 64)
3 128 (?, 4, 4, 128)

Decoder

Los bloques convolucionales Up tienen la estructura:

Dados la salida del bloque anterior Y y la del Bloque Down espejo Xdicc[i-1]

  1. Supermuestrear: Y <- UpSample(Y)

  2. Concatenar: [Y | Xdicc[i-1]

  3. Conv2D 3x3 con activación ReLu con padding para matener la dimensión espacial

  4. Conv2D 3x3 con activación ReLu con padding para matener la dimensión espacial

  5. Dropoout del 25% (parametro definible)

Y=X
for i in range(num_blocks-1,0,-1):
    if i>1:
        numFilters = filters_per_block[i-1] 
    else:
        numFilters = 32
    #print(i, numFilters, Y.shape, Xdicc[i-1].shape)
    Y = UpSampling2D(size=2, name='decoder-up'+str(i))(Y)  
    print(i, numFilters, Y.shape, Xdicc[i-1].shape)
    Y = Concatenate(name='decoder-concat'+str(i))([Y, Xdicc[i-1]])
    Y = Conv2D(numFilters, kernel_size=(3,3), padding='same', activation='relu', name='decoder-conv2'+str(i))(Y)
    Y = Conv2D(numFilters, kernel_size=(3,3), padding='same', activation='relu', name='decoder-conv3'+str(i))(Y)
    Y = Dropout(rate=drop[i], name='decoder-drop'+str(i))(Y)

3 64 (?, 8, 8, 128) (?, 8, 8, 64)
2 32 (?, 16, 16, 64) (?, 16, 16, 32)
1 32 (?, 32, 32, 32) (?, 32, 32, 1)

Tail

El Bloque Tail, contienne dos capas convolucionales: la primera reduce el número de canales preparando el tensor para realizar la clasificación el la capa final de un solo filtro.

# output layers
Y = Conv2D(6, kernel_size=(3,3), 
           padding='same', 
           activation=None,
           name='tail-2xch')(Y)

Y = Conv2D(1, kernel_size=(1,1), 
           padding='same', 
           activation=None, 
           name='tail-last')(Y)
Yout = Lambda(lambda image: tf.image.resize_images(image, (num_rows, num_cols)))(Y)

Construye el modelo del encoder

unet = Model(inputs =Xin,  
                outputs=[Yout], 
                name   ='Unet')
resumen(unet)
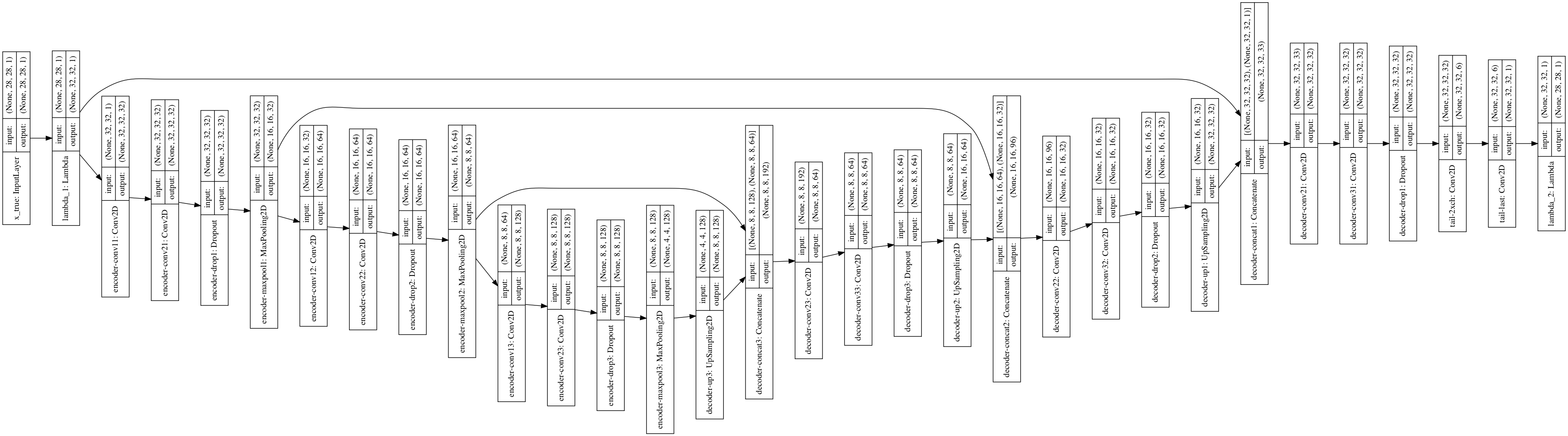
plot_model(unet, to_file='unet.png', show_shapes=True)

==================================================================================
#    Layer Name       Layer Input Shape        Layer Output Shape       Parameters
==================================================================================
0    x_true           (None, 28, 28, 1)        (None, 28, 28, 1)                 0
1    lambda_1         (None, 28, 28, 1)        (None, 32, 32, 1)                 0
2    encoder-conv11   (None, 32, 32, 1)        (None, 32, 32, 32)              320
3    encoder-conv21   (None, 32, 32, 32)       (None, 32, 32, 32)             9248
4    encoder-drop1    (None, 32, 32, 32)       (None, 32, 32, 32)                0
5    encoder-maxpool1 (None, 32, 32, 32)       (None, 16, 16, 32)                0
6    encoder-conv12   (None, 16, 16, 32)       (None, 16, 16, 64)            18496
7    encoder-conv22   (None, 16, 16, 64)       (None, 16, 16, 64)            36928
8    encoder-drop2    (None, 16, 16, 64)       (None, 16, 16, 64)                0
9    encoder-maxpool2 (None, 16, 16, 64)       (None, 8, 8, 64)                  0
10   encoder-conv13   (None, 8, 8, 64)         (None, 8, 8, 128)             73856
11   encoder-conv23   (None, 8, 8, 128)        (None, 8, 8, 128)            147584
12   encoder-drop3    (None, 8, 8, 128)        (None, 8, 8, 128)                 0
13   encoder-maxpool3 (None, 8, 8, 128)        (None, 4, 4, 128)                 0
14   decoder-up3      (None, 4, 4, 128)        (None, 8, 8, 128)                 0
15   decoder-concat3  [(None, 8, 8, 128), (None, 8, 8, 64)] (None, 8, 8, 192)                 0
16   decoder-conv23   (None, 8, 8, 192)        (None, 8, 8, 64)             110656
17   decoder-conv33   (None, 8, 8, 64)         (None, 8, 8, 64)              36928
18   decoder-drop3    (None, 8, 8, 64)         (None, 8, 8, 64)                  0
19   decoder-up2      (None, 8, 8, 64)         (None, 16, 16, 64)                0
20   decoder-concat2  [(None, 16, 16, 64), (None, 16, 16, 32)] (None, 16, 16, 96)                0
21   decoder-conv22   (None, 16, 16, 96)       (None, 16, 16, 32)            27680
22   decoder-conv32   (None, 16, 16, 32)       (None, 16, 16, 32)             9248
23   decoder-drop2    (None, 16, 16, 32)       (None, 16, 16, 32)                0
24   decoder-up1      (None, 16, 16, 32)       (None, 32, 32, 32)                0
25   decoder-concat1  [(None, 32, 32, 32), (None, 32, 32, 1)] (None, 32, 32, 33)                0
26   decoder-conv21   (None, 32, 32, 33)       (None, 32, 32, 32)             9536
27   decoder-conv31   (None, 32, 32, 32)       (None, 32, 32, 32)             9248
28   decoder-drop1    (None, 32, 32, 32)       (None, 32, 32, 32)                0
29   tail-2xch        (None, 32, 32, 32)       (None, 32, 32, 6)              1734
30   tail-last        (None, 32, 32, 6)        (None, 32, 32, 1)                 7
31   lambda_2         (None, 32, 32, 1)        (None, 28, 28, 1)                 0
__________________________________________________________________________________
Total Parameters :  491469
Total Trainable Parameters :  491469
Total No-Trainable Parameters :  0

unet

epochs     = 5        # número de epocas
batch_size = 64        # tamaño del lote
alpha      = 0.0001    # razon de aprendizaje
decay      = 0.0001    # decaimiento de alpha

unet.compile(optimizer =optimizers.adam(lr=alpha, decay=decay),
             loss      = 'mae',
             metrics   = ['accuracy'])

history = unet.fit(x               = X_train,
                   y               = Y_train,
                   batch_size      = batch_size,
                   epochs          = epochs,
                   validation_split= 0.2,
                   verbose         = 1)

Train on 48000 samples, validate on 12000 samples
Epoch 1/5
48000/48000 [==============================] 
- 11s 231us/step 
- loss: 0.0487 
- acc: 0.8138 
- val_loss: 0.0336 
- val_acc: 0.8152
Epoch 2/5
48000/48000 [==============================] 
- 10s 213us/step 
- loss: 0.0345 
- acc: 0.8144 
- val_loss: 0.0304 
- val_acc: 0.8154
Epoch 3/5
48000/48000 [==============================] 
- 10s 213us/step 
- loss: 0.0323 
- acc: 0.8145 
- val_loss: 0.0290 
- val_acc: 0.8154
Epoch 4/5
48000/48000 [==============================] 
- 10s 215us/step 
- loss: 0.0312 
- acc: 0.8146 
- val_loss: 0.0281 
- val_acc: 0.8154
Epoch 5/5
48000/48000 [==============================] 
- 10s 212us/step 
- loss: 0.0305 
- acc: 0.8146 
- val_loss: 0.0276 
- val_acc: 0.8155

# training history
loss = history.history['loss']
acc  = history.history['acc']


epochs = range(1, len(loss) + 1)
plt.figure(2, figsize=(16,5))
plt.subplot(1,2,1)
plt.plot(epochs, loss, 'b.', label='Training loss')
plt.plot(epochs, acc, 'b', label='Validation accuracy')
plt.title('Training and validation MAE loss')
plt.xlabel('Epochs')
plt.ylabel('Loss (MAE)')
plt.legend()


<matplotlib.legend.Legend at 0x7ff024b525f8>

png

Predicciones

import time 
tic = time.time()
Y_train_pred = unet.predict(X_train)
print('\n prediction time for the whole dataset image:', time.time()-tic, 'seconds')

 prediction time for the whole dataset image: 3.971289873123169 seconds

X_train.shape

(60000, 28, 28, 1)

imgs=10

plt.figure(figsize=(14,4))
for i in range(10):
    plt.subplot(3,imgs,i+1)
    idx = list(train_labels).index(i)
    plt.imshow(X_train[idx,:,:,0], 'gray')
    plt.title(train_labels[idx])
    plt.axis('off')

    plt.subplot(3,imgs,i+1+imgs)
    idx = list(train_labels).index(i)
    plt.imshow(Y_train[idx,:,:,0], 'gray')
    plt.axis('off')
    
    plt.subplot(3,imgs,i+1+2*imgs)
    idx = list(train_labels).index(i)
    plt.imshow(Y_train_pred[idx,:,:,0], 'gray')
    plt.axis('off')    
plt.show()

png

Se muestran, en el primer renglon ejemplos de cada dígito de entrada, en el segundo renglón la salida esperada, y el tercer renglon corresponde a la segmentación realizada por la Unet.

Versión Final

import keras
from keras.layers import Input, Dense, Activation, Conv2D
from keras.layers import MaxPooling2D, Dropout, UpSampling2D
from keras.layers import BatchNormalization, Reshape
from keras.layers.merge import Concatenate
from keras.models import Model
from keras.models import Sequential
from keras.utils import plot_model

import numpy as np
import matplotlib.pyplot as plt
import time 

# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
def resumen(model=None):
    '''
    Descipción del modelo en foam compacta (la prefiero a `summary` de keras)
    '''
    header = '{:4} {:16} {:24} {:24} {:10}'.format('#', 'Layer Name','Layer Input Shape','Layer Output Shape','Parameters'
    )
    print('='*(len(header)))
    print(header)
    print('='*(len(header)))
    count=0
    count_trainable=0
    for i, layer in enumerate(model.layers):
        count_trainable += layer.count_params() if layer.trainable else 0
        input_shape = '{}'.format(layer.input_shape)
        output_shape = '{}'.format(layer.output_shape)
        str = '{:<4d} {:16} {:24} {:24} {:10}'.format(i,layer.name, input_shape, output_shape, layer.count_params())
        print(str)
        count += layer.count_params()
    print('_'*(len(header)))
    print('Total Parameters : ', count)
    print('Total Trainable Parameters : ', count_trainable)
    print('Total No-Trainable Parameters : ', count-count_trainable)
    
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Base de Datos Digitos de Mnist
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -


from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

from keras.datasets import mnist

# lectura de los datos
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

print('Dimensiones del conjunto de entrenamiento: ', train_images.shape)
print('Dimensiones del conjunto de evaluación: ',    test_images.shape)

num_data, nrows, ncols = train_images.shape

# binarizaciñon y añadido de ruido

X_train = np.copy(train_images).astype('float64')/255.
Y_train = np.copy(train_images).astype('float64')/255.
X_test  = np.copy(test_images).astype('float64')/255.
Y_test  = np.copy(test_images).astype('float64')/255.

sigma = 0.4
X_train += np.random.normal(loc=0, scale=sigma, size=train_images.shape)
X_test  += np.random.normal(loc=0, scale=sigma, size=test_images.shape)
Y_train = Y_train>0.5
Y_test  = Y_test>0.5

num_test_images, num_rows, num_cols = X_test.shape
X_test.shape

X_train = np.expand_dims(X_train, axis=3)
Y_train = np.expand_dims(Y_train, axis=3)
X_test  = np.expand_dims(X_test,  axis=3)
Y_test  = np.expand_dims(Y_test,  axis=3)

print('Dimensiones de entradas (X) para entrenamiento  (imagenes x rows x cols) =', X_train.shape)
print('Dimensiones de saida (Y) para entrenamiento     (imagenes x rows x cols) =', Y_train.shape)
print('Dimensiones de entradas (X) para evaluación     (imagenes x rows x cols) =', X_test.shape)
print('Dimensiones de saida (Y) para evaluación        (imagenes x rows x cols) =', Y_test.shape)


# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# UNet
# - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

from keras import models
from keras.layers import Conv2D, Dropout, MaxPooling2D, UpSampling2D, Concatenate
from keras import optimizers
from keras.backend import tf as tf
from keras.layers import Lambda, Input


# `filters_per_block` define el número de canales en cada etapa de la Unet, 
# la profundidad de la Unet se adapta de acuerdo a la longitud de dicha lista.
_, num_rows, num_cols, num_channels = X_train.shape
img_dim          = (num_rows, num_cols, num_channels,)
filters_per_block = np.array([num_channels, 32, 64, 128])
num_blocks        = len(filters_per_block)   
kernel_size       = (3,3)
drop              = 0.25*np.ones(num_blocks)


# Encoder

nm= 'encoder'
Xdicc={}

Xin  = Input(shape=img_dim, name="x_true")

X = Lambda(lambda image: tf.image.resize_images(image, (32, 32)))(Xin)
# resize image layer
Xdicc[0] = X
numFilters=filters_per_block[0]
print(0, numFilters, X.shape)

for i in range(1,num_blocks):
    numFilters=filters_per_block[i]
    X = Conv2D(numFilters, kernel_size=kernel_size, padding='same', activation='relu', name='encoder-conv1'+str(i))(X) 
    X = Conv2D(numFilters, kernel_size=kernel_size, padding='same', activation='relu', name='encoder-conv2'+str(i))(X)
    X = Dropout(rate=drop[i], name='encoder-drop'+str(i))(X)
    X = MaxPooling2D(pool_size=(2,2), padding='valid', name='encoder-maxpool'+str(i))(X)
    Xdicc[i] = X
    print(i, numFilters, Xdicc[i].shape) 
      
# Decoder

Y=X
for i in range(num_blocks-1,0,-1):
    if i>1:
        numFilters = filters_per_block[i-1] 
    else:
        numFilters = 32
    #print(i, numFilters, Y.shape, Xdicc[i-1].shape)
    Y = UpSampling2D(size=2, name='decoder-up'+str(i))(Y)  
    print(i, numFilters, Y.shape, Xdicc[i-1].shape)
    Y = Concatenate(name='decoder-concat'+str(i))([Y, Xdicc[i-1]])
    Y = Conv2D(numFilters, kernel_size=(3,3), padding='same', activation='relu', name='decoder-conv2'+str(i))(Y)
    Y = Conv2D(numFilters, kernel_size=(3,3), padding='same', activation='relu', name='decoder-conv3'+str(i))(Y)
    Y = Dropout(rate=drop[i], name='decoder-drop'+str(i))(Y)
    
# Tail 

Y = Conv2D(6, kernel_size=(3,3), 
           padding='same', 
           activation=None,
           name='tail-2xch')(Y)

Y = Conv2D(1, kernel_size=(1,1), 
           padding='same', 
           activation=None, 
           name='tail-last')(Y)
Yout = Lambda(lambda image: tf.image.resize_images(image, (num_rows, num_cols)))(Y)

# construye el modelo
unet = Model(inputs =Xin,  
                outputs=[Yout], 
                name   ='Unet')

# Entrenamiento

epochs     = 5         # número de épocas
batch_size = 64        # tamaño del lote
alpha      = 0.0001    # razon de aprendizaje
decay      = 0.0001    # decaimiento de alpha

unet.compile(optimizer =optimizers.adam(lr=alpha, decay=decay),
             loss      = 'mae',
             metrics   = ['accuracy'])

tic = time.time()
history = unet.fit(x               = X_train,
                   y               = Y_train,
                   batch_size      = batch_size,
                   epochs          = epochs,
                   validation_split= 0.2,
                   verbose         = 1)
print('\n Tiempo de entrenamiento:', time.time()-tic, 'segundos')

# Predicción

tic = time.time()
Y_train_pred = unet.predict(X_train)
print('\n Tiempor de predicción de todos los datos de prueba:', time.time()-tic, 'segundos')