Regresión Logística: la red de una neurona

Mariano Rivera

agosto 2018

Regresión logística

Se muestra una implementación de la regresión logística logística en forma de red neuronal.
El método de regresión logística permite clasificar datos con etiquetas binarias (clasificación binaria), Hastie et. al, 2009.

Representamos por

(1)
${x_i} \in \mathbb{R}^n$
donde asumimos que a todos los datos les hemos agregado un $1$ en su primer entrada $x_{i1} = 1$ y los ordenamos en una matriz $X$ de la forma

(2)
$X = \begin{bmatrix} {x}_1^\top \\ {x}_2^\top \\ {x}_3^\top \\ \vdots \\ {x}_m^\top \end{bmatrix}$
al conjunto de datos vectoriales. Luego contamos para cada dato $x_i$ con la etiqueta

(3)
${y_i} \in \{0, 1 \} \\$
que acomodamos como vector columna $Y \in \{0, 1 \}^{m}$

Datos Iris

Usemos como ejemplo la base de datos Iris. La cual esta disponible en scikit-learn

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn import datasets

iris = datasets.load_iris()

irs

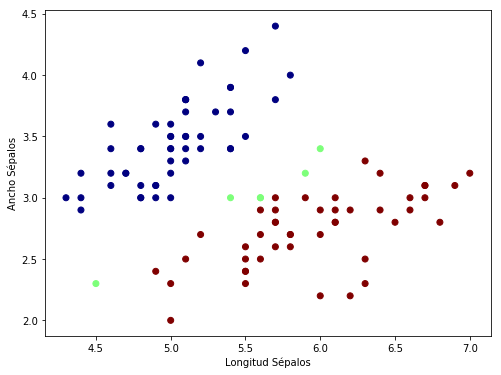
Tomamos los primeros dos valores del vector de rasgos de las primeras dos clases (la base de datos tienen cuatro clases).

idx  = iris.target<2        # primeras dos clases
y    = iris.target[idx]     # {0, 1}
#Y[1] = 1-Y[1]              # cambiamos a un dato su etiqueta
x    = iris.data[idx, :2]   # primeras dos características

plt.figure(figsize=(8, 6))
plt.scatter(x[:, 0], 
            x[:, 1], 
            c=y, 
            cmap=plt.cm.flag)
plt.xlabel('Longitud Sépalos')
plt.ylabel('Ancho Sépalos')
plt.show()

png

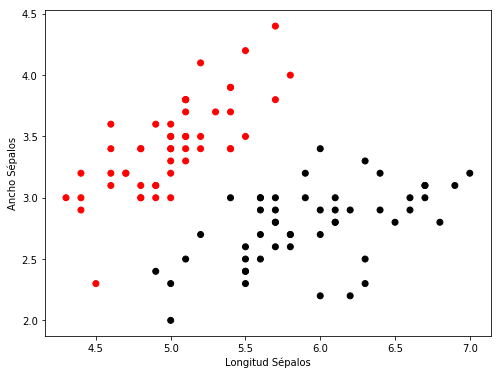
Podemos ver que los datos bidimensionale son linealmente separabes: esto es, existe un plano definido por el vector $w$ ,

(4)
$w_0 + w_1 x_{1,i} + w_2 x_{2,i} = w^\top \begin{bmatrix} 1 \\ x_{1,i} \\ x_{2,i} \end{bmatrix} = w^\top x_i$

en dimensión mayor en uno a la de los datos (por ello agregamos el uno a cada dato), tal que:

(5)

$w^\top x_i \ge 0 \;\;$ si $\;\;y_i=1$ ,
$w^\top x_i < 0 \;\;$ si $\;\; y_i=0$ .

Gráficamente, esto se muestra en la siguiente figura.

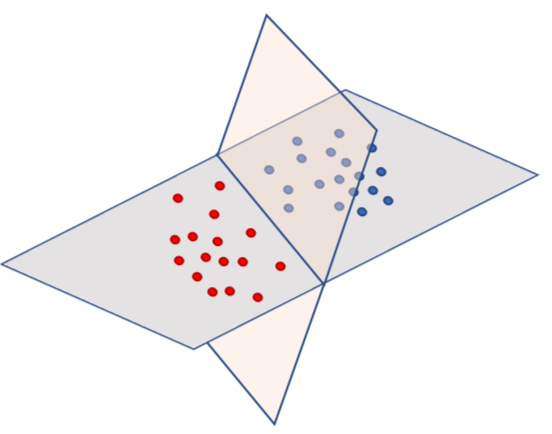
plano separador

Podemos interpretar a $w_1$ y $w_2$ como las pendientes en las del plano, tantas pendientes como dimensiones hay en los datos.
El caso de $w_0$ es más interesante en este caso, pues permite que el plano se desplace y que no tenga que, necesariamente, pasar por el origen.
A $w_0$ le llamaremos bias.

Antes de continuar, introducimos la función sigmoide (que tiene forma de sigma o ‘s’):

(6)
$\phi(z) = \frac{1}{1+exp(-z)}$

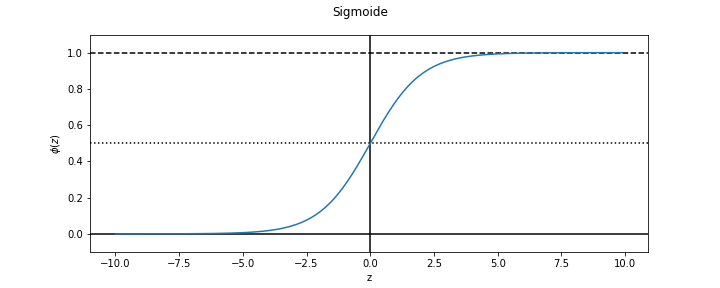
sigmoide

Ahora, usamos el plano separador definido por el vector $w$ como argumento de la función sigmoide, tendremos algo como lo ilustrado en la siguiente figura.

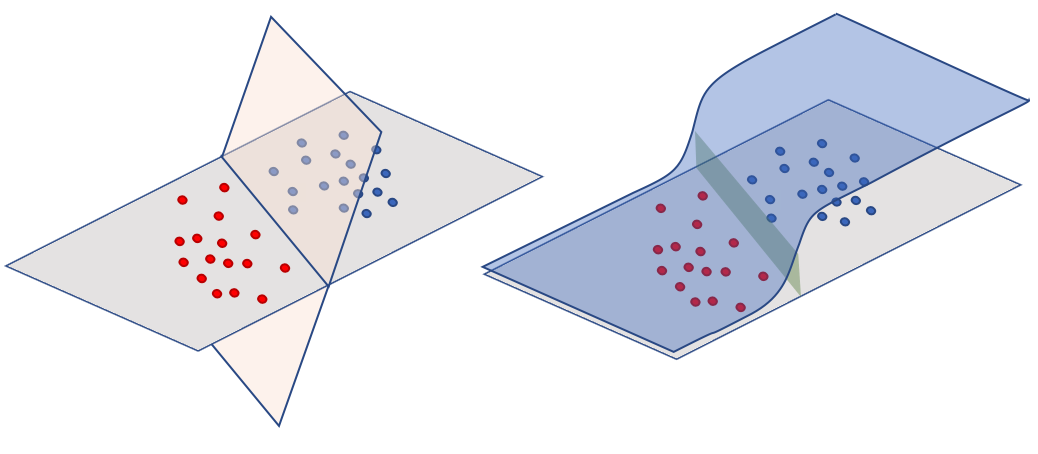
logistica

Si hemos elegido correctamente $w$ resultará que $\phi(w^\top x_i) \approx y_i$ : la sigmoide ajusta los valores de las etiquetas.

Entonces, encontrar el plano separador del conjunto de datos linealmente separable $X$ consiste en resolver el problema de regresión:

(7)
$\underset{w}{\arg\min} \sum_i D[ y_i, \hat y_i]$

donde $\hat y_i$ es el valor

(8)
$\hat y_i \overset{def}{=}\phi(w^\top x_i).$

Queda una duda por resolver, cual es la medida de error o pérdida $D$ a usar en (7). Para ello podemos intrepretamos a $y_i$ como variable aleatoria con distribución Bernoulli (que toma valores $\{0,1\}$ ) y a $\hat y_1$ su predicción, es decir

(11)
$\hat y_i = Prob(y_i=1 | x_i; w) = \phi(w^\top x_i)$
y

(12)
$(1-\hat y_i) = Prob(y_i=0 | x_i; w) = (1-\phi(w^\top x_i))$

Una primera alternativa es usar el Error Cuadrático Medio (Mean Square Error, MSE), quedando (7) de la forma

(9)
$\underset{w}{\arg\min} \sum_i \| y_i - \hat y_1 \|_2^2 + \| (1-y_i) - (1-\hat y_1) \|_2^2 \\ = \underset{w}{\arg\min} \sum_i \| y_i - \hat y_1 \|_2^2 + \| -(y_i-\hat y_1) \|_2^2 \\ = \underset{w}{\arg\min} \sum_i \| y_i - \hat y_1 \|_2^2$

Sin embargo, la correlación cruzada entre dichas variables es mas adecuada:

(10)
$\underset{w}{\arg\min} \sum_i y_i \hat y_1 + (1-y_i) (1-\hat y_1)$

Dado que $y$ esta asociada con clasificar entre dos clases, a (10) se le denomina correlacion cruzada binaria (binary cross-correlation).

Implementación en Keras

import keras
import numpy as np

import matplotlib.pyplot as plt

Una neurona con activación sigmoidal

from keras import models
from keras import layers

logistica = models.Sequential()   

logistica.add(layers.Dense(units= 1,                # numero de neuronas en la capa 
                    activation  = 'sigmoid',        # funcion de activacion = sigmoide
                    name        = 'neurona_unica',  # nombre de la capa  
                    input_shape = (2,)))            # forma de la entrada: (szIm, ) la otra 
                                                    # (dimension del dato, ¿tamano de lote?), 

logistica.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
neurona_unica (Dense)        (None, 1)                 3         
=================================================================
Total params: 3
Trainable params: 3
Non-trainable params: 0
_________________________________________________________________

logistica.compile(optimizer='adam',
                  loss     ='binary_crossentropy',
                  metrics  =['accuracy'])

import time
tic=time.time()

history = logistica.fit(x         = x, 
                        y         = y, 
                        epochs    = 1000, 
                        shuffle   = True,
                        batch_size= 20,
                        verbose   = 0,
                        validation_split=0.2,
                        )

print('Tiempo de procesamiento (secs): ', time.time()-tic)

Tiempo de procesamiento (secs):  4.643330097198486

y_pred = logistica.predict(x).squeeze()

score = logistica.evaluate(x, y, verbose=2)
print('Test loss:',     score[0])
print('Test accuracy:', score[1])

Test loss: 0.35442371606826784
Test accuracy: 0.94

y_pred>0.5

array([False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False,  True, False, False, False,
       False, False, False, False, False,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True, False,  True,  True,  True, False,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True, False, False,  True,  True, False,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True])

plt.figure(figsize=(8, 6))
plt.scatter(x[:, 0], 
            x[:, 1], 
            c=((y_pred>0.5)+y)/2., 
            cmap=plt.cm.jet)
plt.xlabel('Longitud Sépalos')
plt.ylabel('Ancho Sépalos')
plt.show()

png

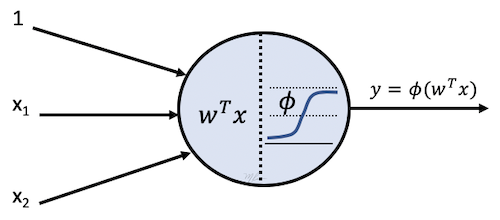
La presente implementación de la regresión logística se puede resumir en la gráfica siguiente:

neurona logistica

Bibliografia

(Hastie et al, 2009) T. Hastie et al., The elements of Statistical Learning, 2nd Ed. Springer, 2009.