Pix2Pix para texturizar imágenes

Mariano Rivera

version 1.0, noviembre 2021

version 1.1, agosto 2022

Citar:

Reyes-Saldana, E., & Rivera, M. (2022). Deep Variational Method with Attention for High-Definition Face Generation. In Mexican Conference on Pattern Recognition (pp. 116-126). Springer, Cham.

View on TensorFlow.org

Pix2pix, propuesto por Isola et al.(2017), es red neuronal profunda que se basa en el entrenamiento tipo GAN de una red tipo UNet. El modelo pix2pix calcula la transformación de una imagen $x$ en una imagen $y$ las cuales difieren, generalmente, en estilo.

Ejemplo de aplicaciones de pix2pix es la transformación entre imágenes aéreas y mapas. Otro ejemplo es generación automática de fachadas de edificios a partir de descipción por bloques (mápa de etiquetas o segmentación semántica). Este último ejemplo es el quese describe en la siguiente figura (Tomada de https://www.tensorflow.org/images/gan/pix2pix_1.png).

sample output_1

La imagen de entrada ( $x$ ) es una mapa de segmentación (mapa descriptivo) de la fachada real (GT) o imagen destino ( $y$ ). Como una etiqueta (color) en mapa descriptivo puede corresponder a muy distintas instancias de la clase (por ejemplo, la etiqueta ventana puede tener muchas correspondencias) Por ello:

No es sensato entrenar la red con una función de ṕerdida que mida el error de la imagen generada ( $x^\prime$ ) respecto a la fachada real ( $y$ ). Por ello es mas razonable evaluar que tan realista resulta la fachada generada.

La propuesta de Isola et al. (2017) consiste en usar como red transformadora de la imagen de entrada $x$ a una imágen predicha ( $x'$ ) una una red UNet; Ronnenberg et al. (2015). Asuminedo $y$ la imagen verdarera que corresponde a $y$ , se utiliza una red Discriminadora para evaluar los pares de imágenes verdaderos $(x,y)$ y los sintéticos $(x, x')$ .

Referencias

(Isola, 2017) Phillip Isola et al. “Image-to-image translation with conditional adversarial networks”. In: Proceedings of the IEEE conference on computer vision and pattern recognition. 2017, pp. 1125–1134

(Ronnenberg et al., 2015) Olaf Ronnenberg et al., U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proc. ICCAI, Springer, LNCS 9351, pp. 234–241.

(Reyes-Saldana & Rivera, 2022) Reyes-Saldana, E., & Rivera, M. (2022). Deep Variational Method with Attention for High-Definition Face Generation. In Mexican Conference on Pattern Recognition (pp. 116-126). Springer, Cham.

Problema a resolver

En esta variante que presentamos de pix2pix la tarea será la de incorporar textura en imágenes generadas por la VAE.

En ese ejemplo usamos datos de Celeb-A de Alta definición (HQ). Esos datos se codifican en un espacio latente de dimensión 128. Dicho vector normal-gaussiano com media 0 y desviación estándard 1. Luego, un Decodificador genera los datos a partir de vectores muestreados en el espacio latente. En la figura a continuación muestra un dato original y su reconstrucción a partir de su codificación.

vae_in_out

Ahora es incorporar en la imaged generada por la VAE textura tal que luzca tan realista (no necesariamnete igual) como a imagen original. Para ello usaremos el modelo pix2pix. Dicho modelo se puede representar gráficamente por el siguiente diagrama.

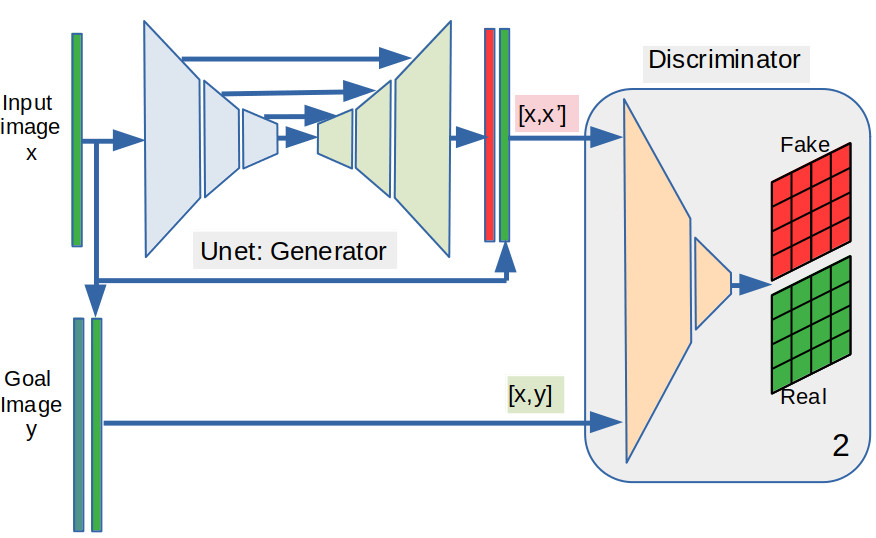
Generator Update Image

De acuerdo al diagrama de arriba, para entrenar el modelo pix2pix, es necesario dar como entradas tanto la imágen en el dominio de entrada $x$ como la del dominio de salida $y$ . Luego cada vez que se realiza una predicción (de transformación) $x'$ , se generan dos pares de imágenes, uno que contienen las imágenes reales ( $x,y$ ) y otro conformado por la entrada y la predicción ( $x,x'$ ). Ambas imágenes son evaluadas por la red totalmente convolucional Discriminadora para producir un tensor 2D de dimensiones ( $h \times w$ ). Cada elemento del tensor salida del Discriminador toma valores en el intervalo $[0,1]$ , por lo que puede interpretarse como la probabilidad de que la región de soporte tiene las características (que dicha respuesta evalúa) de un par real. No podemos saber de antemano que características evalúa cada elemento de la respuesta del discriminador: estos extractores de carácterísticas se entrenan dependiendo de la tarea.

Lo interesante es que se analiza los pares de imágenes región (de soporte) por región (de soporte), cada región puede tener una calificación diferente de “verasidad”.

La tarea del Disciminador es distinguir entre regiones que pertenecen al par real y del sintético. Mientras que la tarea del Generador es producir imágenes tan realistas como sea posible que confundan al Discriminador.

Dado que idealmente el Discriminador produce una tensor de puros ceros si el par evaluado es sintético y de puros unos si es real, la función de costo implica calcular la entropía cruzada (cross-entropy).

Implementacion de pix2pix (ejemplo de tf)

A continuación presentamos nuestra versión comentadad del código ejemplo de tensorflow para pix2pix.

Iniciamos cargando librerías que usaremos.

import os
from glob import glob
import numpy as np
import matplotlib.pyplot as plt
import pathlib
import time
import datetime
from IPython import display


import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

Definimos variables globales de nuestra implementación:

Tamaño de las imágenes a procesar ( $x,y,x'$ ).
Número de canales de la imagen de salida, por si acaso fuera distinto al de la imagen de entrada.
Tamaño del lote, se ha visto que el modelo pix2pix funciona adecuadamente con tamaños de lote pequeños, inclusive de tamaño 1.
Número de épocas.
Época de inicio (por si acaso retomamos el entrenamietos y desemos continuar con la numeración).

INPUT_DIM     = (256,256,3)
OUTPUT_CHANNELS = INPUT_DIM[-1]   
BATCH_SIZE    = 10
R_LOSS_FACTOR = 10000
EPOCHS        = 100
INITIAL_EPOCH = 0

Ubicamos los datos:

El directorio X_FOLDER contiene los datos de las imágenes de entrada.
El directorio Y_FOLDER contiene los datos de las imágenes de objetivo.

Asumimos que ambos directorios contienen el mísmo número de imágenes y que una vez ordenados el listado de archivos en cada directorio, los archivos se corresponden 1 a 1.

El directorio DIR_MODELS será donde almacenaremos el modelo que durante el entrenamiento tenga el mejor resultado parcial

# run params
X_FOLDER      = "/home/mariano/Data/CelebAMask-HQ/CelebA-HQ-vae-256/"
Y_FOLDER      = "/home/mariano/Data/CelebAMask-HQ/CelebA-HQ-img-256/"
DIR_MODELS    = "./results_vae_unet_hq_256_z128/models"

Creamos las listas de archivos en los directorios con la imágenes con que trabajaremos.

xfiles  = glob(os.path.join(X_FOLDER, '*.jpg'))
yfiles  = glob(os.path.join(Y_FOLDER, '*.jpg'))
xfiles.sort()
yfiles.sort()
xfiles=np.array(xfiles)
yfiles=np.array(yfiles)

A modo de validación, imprimimos los primeros 5 nombres en cada lista. Los directorios serán distintos, pero los nombres de los archivos son iguales.

[print(x, y) for x,y in zip(xfiles[:5],yfiles[:5])];

/home/mariano/Data/CelebAMask-HQ/CelebA-HQ-vae-256/0.jpg /home/mariano/Data/CelebAMask-HQ/CelebA-HQ-img-256/0.jpg
/home/mariano/Data/CelebAMask-HQ/CelebA-HQ-vae-256/1.jpg /home/mariano/Data/CelebAMask-HQ/CelebA-HQ-img-256/1.jpg
/home/mariano/Data/CelebAMask-HQ/CelebA-HQ-vae-256/10.jpg /home/mariano/Data/CelebAMask-HQ/CelebA-HQ-img-256/10.jpg
/home/mariano/Data/CelebAMask-HQ/CelebA-HQ-vae-256/100.jpg /home/mariano/Data/CelebAMask-HQ/CelebA-HQ-img-256/100.jpg
/home/mariano/Data/CelebAMask-HQ/CelebA-HQ-vae-256/1000.jpg /home/mariano/Data/CelebAMask-HQ/CelebA-HQ-img-256/1000.jpg

Por razones de eficiencia, usaremos la librería tensorflow.datasets para administrar la lectura de archivos. Para ello definimos las siguentes variables globales.

BUFFER_SIZE con el número total de (pares de) imágenes a procesar. Esto permitira que datasets pueda administrar adecuadamente la memoria de la CPU para cargar anticipadamente los datos.
Dado que sobrecargaremos el método fit, la variable step_per_epoch nos indicará cuando se habrá concluido una época. Pues los datos se cargan por dataset asumiendo una stream infinita.

BUFFER_SIZE      = len(xfiles)
steps_per_epoch  = BUFFER_SIZE //BATCH_SIZE
print('num image files : ', BUFFER_SIZE)
print('steps per epoch : ', steps_per_epoch )

num image files :  30000
steps per epoch :  3000

Pix2pix: Traducción de Imagen-a-Imagen con una GAN condicional

Como dijimos, usaremos librerías de Tensorflow para cargar la imágenes y preprocesarlas. Ello nos permite usar estos procedimientos eficientemente con la librería datasets.

Las imágenes están en formato jpg por lo que leeremos el archivo con tf.io.read_file y posteriormente decodificamos es stream de bytes con tf.image.decode_jpeg.

Se transforman a float32, en dimensión ( $256 \times 256$ ) y con valores en el intervalo $[-1,1]$ .

En pix2pix paper realizan como aumentación de datos un flip horizontal aleatorio (izq. $\leftrightarrow$ der.).

A continuación definimos dos funciones auxilares para cargar los datos y guardar reusultados parciales en forma de mosaico.

def load_images(xfile, yfile, flip=True):
    '''
    Lee par de imagenes jpeg y las reescala la tamaño deseado 
    
    Aumantación: Flip horizontal aleatorio, sincronizado
    '''
    
    xim = tf.io.read_file(xfile)
    xim = tf.image.decode_jpeg(xim)
    xim = tf.cast(xim, tf.float32)
    xim = xim/127.5-1 
    '''
    # en caso de ser necesario cambiar las dimensiones de la imagen x al leerla
    xim = tf.image.resize(xim, INPUT_DIM[:2],
                            method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
    # en caso de ser necesario cambiar las dimensiones de la imagen y al leerla
    yim = tf.image.resize(yim, INPUT_DIM[:2],
                            method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
    ''';
    
    yim = tf.io.read_file(yfile)
    yim = tf.image.decode_jpeg(yim)
    yim = tf.cast(yim, tf.float32)
    yim = yim/127.5-1    
    
    # Aumentación sincronizada de dada imágen del par $(x,y)$, en este caso solo un flip der-izq
    if flip and tf.random.uniform(()) > 0.5:
        xim = tf.image.flip_left_right(xim)
        yim = tf.image.flip_left_right(yim)
    
    return xim, yim

def display_images(x_imgs=None, y_imgs=None, rows=4, cols=3, offset=0):
    '''
    Despliega pares de imágenes tomando una de cada lista 
    '''
    plt.figure(figsize=(cols*5,rows*2.5))
    for i in range(rows*cols):
        plt.subplot(rows, cols*2, 2*i+1)
        plt.imshow((x_imgs[i+offset]+1)/2)
        plt.axis('off')
    
        plt.subplot(rows, cols*2,2*i+2)
        plt.imshow((y_imgs[i+offset]+1)/2)
        plt.axis('off')
                      
    plt.tight_layout()
    plt.show()

Imágenes de ejemplo

Pares de imágenes ( $x,y$ ), imagen entrada y su imagen destino.

rows=2
cols=2

x_imgs=[]
y_imgs=[]

for i in range(rows*cols):
    xim, yim = load_images(xfiles[i], yfiles[i])
    x_imgs.append(xim)
    y_imgs.append(yim)
    
print(x_imgs[0].shape, x_imgs[0].shape) # a modo de comprobacion

(256, 256, 3) (256, 256, 3)

Deplegamos pares de imagenes $(x,y)$ y comentamos abajo algunos detalles.

display_images(x_imgs, y_imgs, rows=rows, cols=cols)

png

Como podemos observar, la imagen de entrada parece ser una versión “suavizada” de la imagen destino. Pero no es simplemente un suavizado el que las distingue. Podemos notar que la expresión de los rostros puede cambiar (por ejemplo la sonrisa de la rubia de arriba a derecha no esta presente en el rostro suavizado, ni el color de los ojos corresponde. Notamos que no existe una correspondencia exacta Pixel-a-Pixel entre las imágenes ( $x,y$ ). Lo mismo podemos decir para los demás rostros. La tarea que resolveremos será la de incluir textura en las imágenes “suaves”, con ello llevaremos al límite al modelo pix2pix. Veamos que puede hacer el modelo.

Datasets para Entrenamiento-Validación y Prueba

Con el 80% de la lista creamos primero un tf.Dataset de entrenamiento/validación para los archivos de entrada (codificados) y otro para los objetivo (reales). Estos datasets estan ordenados tal que los archivos corresponden uno a uno.

idx = int(BUFFER_SIZE*.8)

train_x = tf.data.Dataset.list_files(xfiles[:idx],shuffle=False)
train_y = tf.data.Dataset.list_files(yfiles[:idx],shuffle=False)

Luego, creamos un tercer dataset que empareja los elementos de los anteriores datasets. Este dataset es creado con un zip de los dos primeros. Ahora si podemos permitir que sean remezclados en cada época (shuffle).

El dataset se conforma con pares de nombres de archivos, con idéntico nombre (en este caso) pero almacenados en distintos directorios. Leemos cada elemento del dataset al hacer map de la lectura cada elemento del nuevo data set (pareja de nombres de archivos).

train_xy = tf.data.Dataset.zip((train_x, train_y))
train_xy = train_xy.shuffle(buffer_size=idx, reshuffle_each_iteration=True)
train_xy = train_xy.map(load_images, num_parallel_calls=tf.data.AUTOTUNE)
train_xy = train_xy.batch(BATCH_SIZE)

Igual procedemos para el restante 20% de archivos que conforman el dataset de prueba (test).

test_x = tf.data.Dataset.list_files(xfiles[idx:],shuffle=False)
test_y = tf.data.Dataset.list_files(yfiles[idx:],shuffle=False)

test_xy = tf.data.Dataset.zip((test_x, test_y))
test_xy = test_xy.map(load_images, num_parallel_calls=tf.data.AUTOTUNE)
test_xy = test_xy.batch(BATCH_SIZE)

Comprobamos que el objeto datset que lee pares de imágenes de directorios distintos esta sincronizado.

rows=2
cols=2
for x,y in train_xy.take(1):
    display_images(x, y, rows=rows, cols=cols)
    break

png

Generator

El generador pix2pix cGAN es una modificación de la U-Net.

Bloque de codificación (down-sampling)

def downsample(filters, size, apply_batchnorm=True):
    '''
    Bloque de codificación (down-sampling)
    '''
    initializer = tf.random_normal_initializer(0., 0.02)

    result = tf.keras.Sequential()
    result.add(tf.keras.layers.Conv2D(filters           = filters, 
                                      kernel_size       = size, 
                                      strides           = 2, 
                                      padding           = 'same',
                                      kernel_initializer= initializer, 
                                      use_bias          = False))

    if apply_batchnorm:
        result.add(tf.keras.layers.BatchNormalization())

    result.add(tf.keras.layers.LeakyReLU())

    return result

Validamos el bloque de codificación

down_model  = downsample(3, 4)
down_result = down_model(tf.expand_dims(xim, 0))
print(down_result.shape)

(1, 128, 128, 3)

Bloque de decodicación (up-sampling)

def upsample(filters, size, apply_dropout=False):
    '''
    Bloque de decodicación (up-sampling)
    '''
    initializer = tf.random_normal_initializer(0., 0.02)

    result = tf.keras.Sequential()
    result.add(tf.keras.layers.Conv2DTranspose(filters           = filters, 
                                               kernel_size       = size, 
                                               strides           = 2,
                                               padding           = 'same',
                                               kernel_initializer= initializer,
                                               use_bias          = False))

    result.add(tf.keras.layers.BatchNormalization())

    if apply_dropout:
        result.add(tf.keras.layers.Dropout(0.5))

    result.add(tf.keras.layers.ReLU())

    return result

up_model = upsample(3, 4)
up_result = up_model(down_result)
print (up_result.shape)

(1, 256, 256, 3)

Las dimensiones son correctas, se downsample reduce el alto y ancho de los tensores en la mitad y upsample las incrementa al doble.

Generador UNet

def Generator():
    '''
    UNet
    '''
    
    # Capas que la componen
    x_input = tf.keras.layers.Input(shape=INPUT_DIM)
    down_stack = [
        downsample(64,  4, apply_batchnorm=False),# (batch_size, 128, 128, 64)
        downsample(128, 4),                       # (batch_size, 64,  64,  128)
        downsample(256, 4),                       # (batch_size, 32,  32,  256)
        downsample(512, 4),                       # (batch_size, 16,  16,  512)
        downsample(512, 4),                       # (batch_size, 8,   8,   512)
        downsample(512, 4),                       # (batch_size, 4,   4,   512)
        downsample(512, 4),                       # (batch_size, 2,   2,   512)
        downsample(512, 4),                       # (batch_size, 1,   1,   512)
    ]

    up_stack = [
        upsample(512, 4, apply_dropout=True),     # (batch_size, 2,    2,  1024)
        upsample(512, 4, apply_dropout=True),     # (batch_size, 4,    4,  1024)
        upsample(512, 4, apply_dropout=True),     # (batch_size, 8,    8,  1024)
        upsample(512, 4),                         # (batch_size, 16,   16, 1024)
        upsample(256, 4),                         # (batch_size, 32,   32, 512)
        upsample(128, 4),                         # (batch_size, 64,   64, 256)
        upsample(64,  4),                         # (batch_size, 128, 128, 128)
    ]

    initializer = tf.random_normal_initializer(0., 0.02)
    last = tf.keras.layers.Conv2DTranspose(OUTPUT_CHANNELS, 4,
                                         strides=2,
                                         padding='same',
                                         kernel_initializer=initializer,
                                         activation='tanh')  # (batch_size, 256, 256, 3)

    # pipeline de procesamiento
    x = x_input
    # Codificador
    skips = []
    for down in down_stack:
        x = down(x)
        skips.append(x)  # se agrega a una lista la salida cada vez que se desciende en el generador
    skips = reversed(skips[:-1])
    # Decodificador
    for up, skip in zip(up_stack, skips):
        x = up(x)
        x = tf.keras.layers.Concatenate()([x, skip])

    x = last(x)

    return tf.keras.Model(inputs=x_input, outputs=x)

Arquitectura del generador (UNet).

generator = Generator()
tf.keras.utils.plot_model(generator, show_shapes=True, dpi=64)

png

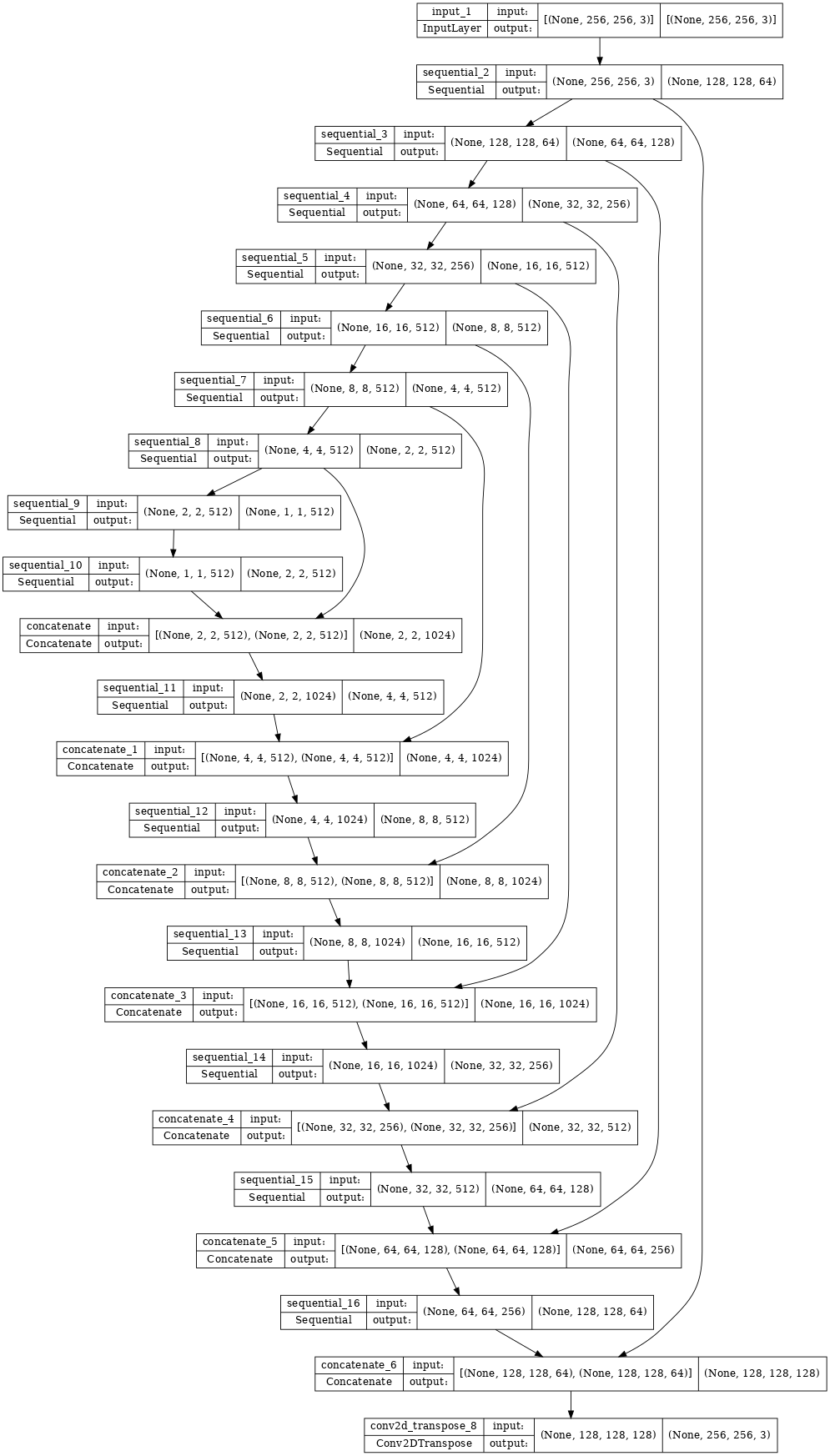
Probamos el generador pasando un dato a través de la red. Por el momento no esperemos resultados notables pues los pesos tienen valores aleatorios: solo que la entrada puede ser procesada; es decir, que hayamos construido el modelo correctamente.

gen_output = generator(xim[tf.newaxis, ...], training=False)
plt.imshow(gen_output[0, ...]*50)

png

A modo de recordatorio, repetimos el diagrama del modelo que implementamos a continuación.

Generator Update Image

En este diagrama $x'$ es un dato aproximado y $y$ es el dato real. Recordando nuestra tarea, pretendemos añadir a $x$ características tal que el resultado $x'$ sea semejante a $y$ , no necesariamente igual.

$y \approx x^\prime = x+C$

Es decir, que parezca que $x'$ es generado a partir de la misma distribución que $y$ . Esto es, si $y \sim P(Y)$ , entonces queremos $x^\prime \sim P(Y)$ .

Luego, sea $P(Y)$ la distribución real de donde vienen el dato real $y$ , y $x$ el dato aproximado generado con $P(X)$ conocida (en ets caso un VAE), entonces:

$P(Y) = P(Y|X) P(X)$

Para completar el lado derecho de la igualdad, vamos a aproximar la probabilidad condicional $P(Y|X)$ por una función determinística:

$P(Y|X) = G(X; W)$
donde $G$ es el generador y $W$ sus parámetros (pesos de la red). Todo el componente aleatorio para generar $x^\prime$ será responsabilidad de $P(X)$ .

Finalmente, para encontrar este generador usamos un enfoque del tipo Redes Generadoras Antagónicas (GAN).

Discriminador

El discriminador que usamos es una red convolucional que tiene como salida un tensor 2D (en este caso de 1 canal). Cada salida en el discriminador se calcula usando un parche de la imagen de entrada como soporte. Cada salida es responsable de indicar si su soporte corresponde a un par que contiene a la image real $y$ o a la imagen sintética $x$ . Ver pix2pix paper.

Es importante notar que:

El discriminador procesa un par de entrada y produce un tensor de salida.
Aunque para cada imagen $x$ procesada por $G$ se invoca dos veces: una para evaluar el par con datos generados y la otra para evaluar el par con datos reales. En realidad procesa por lotes, no por pares, pero ese detalle no es necesario para entender el funcionamiento de pix2pix.
Reusamos los bloques downsample: Conv2D (con submuestreo) -> BatchNormalization -> LeakyReLU obteniendo una salida de (batch_size, 30, 30, 1).
Por conveniencia, a salida del Discriminador se pone una activación sigmoidal, sino que se deja lineal para interpretar como logits, valores reales en el intervalo $(-\infty, \infty)$ .

def Discriminator():
    initializer = tf.random_normal_initializer(0., 0.02)

    inp = tf.keras.layers.Input(shape=[256, 256, 3], name='input_image')
    tar = tf.keras.layers.Input(shape=[256, 256, 3], name='target_image')
    x = tf.keras.layers.concatenate([inp, tar])  # (batch_size, 256, 256, channels*2)

    down1 = downsample(64, 4, False)(x)  # (batch_size, 128, 128, 64)
    down2 = downsample(128, 4)(down1)    # (batch_size, 64, 64, 128)
    down3 = downsample(256, 4)(down2)    # (batch_size, 32, 32, 256)

    zero_pad1 = tf.keras.layers.ZeroPadding2D()(down3)  # (batch_size, 34, 34, 256)
    conv = tf.keras.layers.Conv2D(512, 4, strides=1,
                                kernel_initializer=initializer,
                                use_bias=False)(zero_pad1)  # (batch_size, 31, 31, 512)
    batchnorm1 = tf.keras.layers.BatchNormalization()(conv)
    leaky_relu = tf.keras.layers.LeakyReLU()(batchnorm1)
    
    zero_pad2 = tf.keras.layers.ZeroPadding2D()(leaky_relu)  # (batch_size, 33, 33, 512)
    last = tf.keras.layers.Conv2D(filters    =1, 
                                  kernel_size=4, 
                                  strides    =1,
                                  kernel_initializer=initializer)(zero_pad2)  # (batch_size, 30, 30, 1)

    return tf.keras.Model(inputs=[inp, tar], outputs=last)

discriminator = Discriminator()
tf.keras.utils.plot_model(discriminator, show_shapes=True, dpi=64)

png

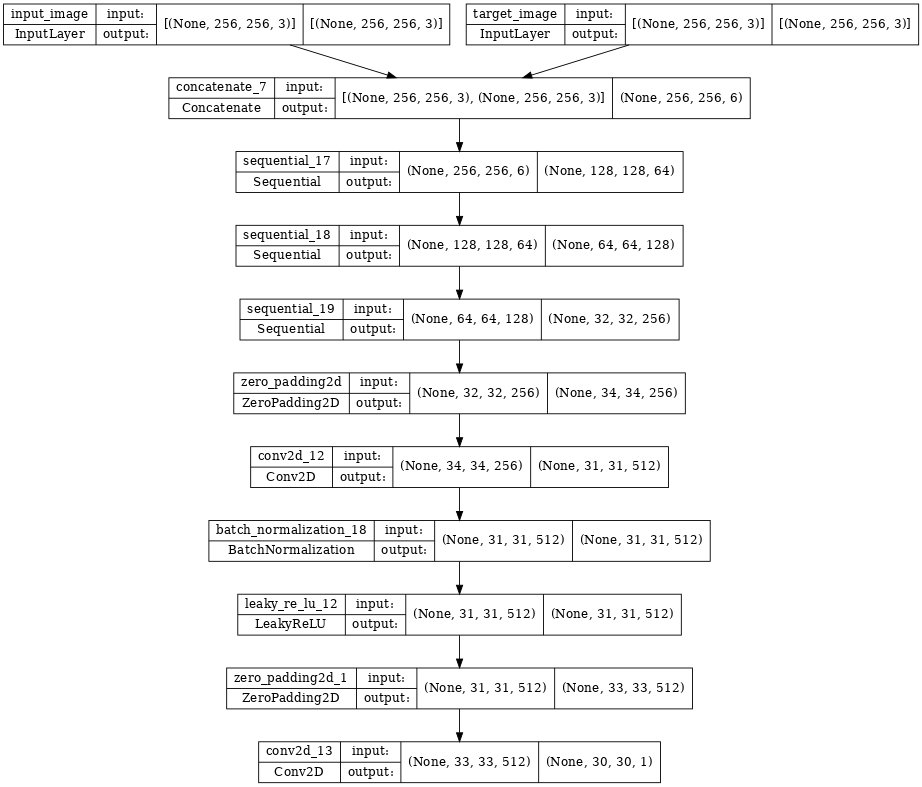
Notemos que en este caso, tenemos un arreglo de semáforos de ( $30 \times 30$ ), cada uno indicando si el par de entrada en la región de soporte es es real o generado.

Es posible que el Generador (Unet) logre engañar al Discriminador en algunas regiones y no en otras. Por lo que en el entrenamiento, los pesos del Discrimimador se ajustaran para detectar mejor las regiones en que fue engañado. Por otro lado, el Generador se enfocará a mejorar las regiones en que lo han descubierto.

Probamos el Discriminador pasando la salida “dummy” del generador. Sólo es para pobar que esté corectamente implementado, los pesos aun son aleatorios.

disc_out = discriminator([xim[tf.newaxis, ...], gen_output], training=False)

plt.figure(figsize=(10,5))
plt.subplot(121)
plt.imshow((xim+1)/2)
plt.subplot(122)
plt.imshow(disc_out[0, ..., -1]*200, vmin=-20, vmax=20, cmap='RdBu_r')  #*100
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7f8c717e0430>

png

Funciones de Pérdida (Losses) de la GAN

En el ejemplo de tensorflow se emplea una pérdida que:

Compara la imagen generada con la real mediante (evalua el mapeo pix2pix) usando MSE (L1). En nuestro problema esto no tenen sentido dado que no pretendemos generar la imagen exacta original, sino solo imponer textura en la imagen aproximada $x$ (generada por el VAE).

2 Calcula la entropía-cruzada binaria entre cada elemento de la salida del discriminador y un 1.

Para entrenar el generador queremos que cada región de la imagen generada sea realista. Es decir, la pérdida del generador mide la discordancia entre la salida del discriminador y el vector de 1’s

Para entrenar el discriminador medimos de su salida:

La concordancia (signo negativo) con un el vector de 1’s. Diríamos que el generador le pasó un strike al discriminador.
La discordancia con un el vector de 1’s, debe detectar como reales los reales.

Resumiedo nuestra estrategia:

Contamos con pares de datos $(x,y)$
Para cada dato $x$ realizamos una predicción (imagen con textura) $\hat y$ mediante el generador, $G$ .
Luego el discriminador $D$ obtienen un tensor que califica la veracidad de un parche (de soporte) en $y$ real y la predicción $\hat y$ ; digamos que la salida para el $i$ -ésimo dato la denotamos $\hat z_i \in [0,1]$ .
Lo que esperamos es que el discriminador aproxime con $\hat z$ a $z = \mathbf{1}$ si dato es real, y a $\hat z = \mathbf{0}$ si el dato es sintético.
El costo del discriminador lo calcularemos mediate la entropía cruzada (crossentropy):

$L (\hat z ) = - \frac{1}{N}\sum_{i:z_i=1} z_i \log \hat z_i - \frac{1}{N}\sum_{i:z_i=0} (1-z_i) \log (1-\hat z_i)$
donde $N$ es el número de pares imágenes de entrenamiento.

Demos un paso mas para simplificar la red. Asumimos que el discriminador calcula los logits $\alpha$ en vez de las probabilidades:
$\alpha_i = \log \hat z_i \in (-\infty, \infty).$
Luego la pérdidad del discriminador estará dada por:
$L (\hat z ) = - \frac{1}{N} \sum_{i: z_i\in \{0, 1\}} \alpha_i.$
Consecuentemente, la pérdidad del generdor queda
$L (\hat z ) = - \frac{1}{N} \sum_{i:z_i=0} \alpha_i.$

Por ello usamos

loss_object = tf.keras.losses.BinaryCrossentropy(from_logits=True)

Loss del Discriminador

def discriminator_loss(disc_real_output, disc_generated_output):
    real_loss        = loss_object(tf.ones_like(disc_real_output), disc_real_output)
    generated_loss   = loss_object(tf.zeros_like(disc_generated_output), disc_generated_output)
    total_disc_loss  = real_loss + generated_loss
    return total_disc_loss

Loss del Generador

En el caso de la ṕérdida del generador, con el fin de guiar la predicción incluimos el error de reconstrucción
$L (\hat z ) = - \frac{1}{N} \sum_{i:z_i=0} \alpha_i + \Lambda \, MAE(y, x^\prime)$
donde MAE es la Media de los Errores Absolutos y $\Lambda$ es un parámetro positivo que pesa la contribución de cada término.

LAMBDA = 100

def generator_loss(disc_generated_output, gen_output, target):
    '''
    el generador debe entrenarse para maximizar los errores de detección de imágenes sintéticas
    '''  
    # Entropia cruzada a partir de logits
    gan_loss = loss_object(tf.ones_like(disc_generated_output), disc_generated_output)

    # Media de los Errores Absolutos
    l1_loss = tf.reduce_mean(tf.abs(target - gen_output))

    total_gen_loss = gan_loss + (LAMBDA * l1_loss)

    return total_gen_loss, gan_loss, l1_loss

Optimizadores

Usamos el algoritmo Adam tanto para el generador como al discriminador. Dichas optimizaciones se realizan en paralelo (evolucionan en forma distinta) por lo que requerimos dos instancias de Adam.

generator_optimizer     = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
discriminator_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)

Puntos de control (Checkpoints)

Durante el entrenamiento monitoramos el proceso e iremos guardaremos (salvamos en arhivo) los valores de los pesos de el discriminador y el generador.

checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
                                 discriminator_optimizer=discriminator_optimizer,
                                 generator=generator,
                                 discriminator=discriminator)

Definimos una función para ir desplegando los avances del algoritmo.

def generate_images(model, x_input, y_input):
    '''
    Con training=True se obtienen las metricas sobre el Lote. 
    En otro caso, no se evaluan y se regresan las del entrenamiento.
    '''
    y_pred= model(x_input, training=True)  
    
    
    plt.figure(figsize=(15, 15))
    display_list = [ y_input[0], x_input[0], y_pred[0]]
    title        = ['Objetivo, $y$', 'VAE $x$', 'P2P  $x^\prime$']
    for i in range(3):
        plt.subplot(1, 3, i+1)
        if i<3: 
            plt.title(title[i])
        # Getting the pixel values in the [0, 1] range to plot.
        plt.imshow((display_list[i]+1)/2)
        plt.axis('off')
    plt.show()

Probamos la función

for x_input, y_input in train_xy.take(1):
    generate_images(generator, x_input, y_input)
    print(x_input.shape, y_input.shape)
    break

png

(10, 256, 256, 3) (10, 256, 256, 3)

Podemos constatar que al menos completa el procesamiento. Dado que no hemos entrenado el modelo (los pesos todavía son aleatorios), el resultado ( $x^\prime$ ) aún no tiene significado.

Entrenamiento

Basados el el proceso arriba ilustrado, usaremos para el entrenamiento una estrategia del tipo Generador por Redes Adversarias (GAN).

log_dir="logs/"

summary_writer = tf.summary.create_file_writer(
  log_dir + "fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S"))

A continuación se muestra la función que se llama a cada paso de entrenamiento. Esta función recibe pares de imágenes $(x,y)$ de entrada.

@tf.function
def train_step(input_image, target, step):
    '''
    Cálculos realizados durante un paso del entrenamiento
    
    Dadas los pares x,y (suavizada, real):
    - Genera datos sintéticos x' con Unet
    - Evalua el discriminador para los pares suavizado-(x,y) y texturizado-(x',y) 
    - Evalua los costos del generador y del discriminador
    - Calcula los gradiente
    - Realiza los pasos de optimización
    - Reporta loss y métricas
    '''
    
    with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
    
        gen_output = generator(input_image, training=True)

        disc_real_output      = discriminator([input_image, target],     training=True)
        disc_generated_output = discriminator([input_image, gen_output], training=True)

        gen_total_loss, gen_gan_loss, gen_l1_loss = generator_loss(disc_generated_output, gen_output, target)
        disc_loss = discriminator_loss(disc_real_output, disc_generated_output)

    generator_gradients     = gen_tape.gradient(gen_total_loss, generator.trainable_variables)
    discriminator_gradients = disc_tape.gradient(disc_loss,     discriminator.trainable_variables)

    generator_optimizer.apply_gradients(    zip(generator_gradients,     generator.trainable_variables))
    discriminator_optimizer.apply_gradients(zip(discriminator_gradients, discriminator.trainable_variables))

    with summary_writer.as_default():
        ss = step//1000
        tf.summary.scalar('gen_total_loss', gen_total_loss, step=ss)
        tf.summary.scalar('gen_gan_loss',   gen_gan_loss,   step=ss)
        tf.summary.scalar('gen_l1_loss',    gen_l1_loss,    step=ss)
        tf.summary.scalar('disc_loss',      disc_loss,      step=ss)

¡No usamos el método fit de keras!

Ahora definimos el lazo (loop) completo de entrenamiento que invoca al paso de entrenamiento. Esta función es tal cual se propone en el ejemplo de tensorflow:

Iterar un número de pasos (steps)
Cada 10 iteraciones imprime un punto ‘.’
Cada 1K iteraciones muestra el progreso al desplegar la imagen generada.
Cada 5K iteraciones guarda los pesos (checkpoint).

def fit(train_xy, test_xy, steps):
    
    # toma un lote, batch de pares (x,y)
    x, y = next(iter(test_xy.take(1)))
    start = time.time()

    for step, (x, y) in train_xy.repeat().take(steps).enumerate():
        
        # muestra avance en la texturización 
        if (step) % 1000 == 0:
            display.clear_output(wait=True)
            if step != 0: 
                print(f'Time taken for 1000 steps: {time.time()-start:.2f} sec\n')
            
            start = time.time()
            generate_images(generator, x,y)  
            print(f"Step: {step//1000}k")

        # paso de entrenamiento
        train_step(x,y, step)
        if (step+1) % 10 == 0: print('.', end='', flush=True)

        # Checkpoint every 5k steps
        if (step + 1) % 5000 == 0:
              checkpoint.save(file_prefix=checkpoint_prefix)

Usando TensorBoard para monitorear el entrenamiento

Tensorboardse debe lanzar antes de iniciar el entrenamiento. Ejecutar los siguientes comandos en una celda de código.

%load_ext tensorboard
%tensorboard --logdir {log_dir}

Ahora realizamos propiamente la iteración de entrenamiento. Desplegamos resultados conforme progresamos.

fit(train_xy, test_xy, steps=80000)

Time taken for 1000 steps: 68.63 sec

png

Step: 79k
....................................................................................................

Durante el entrenamiento es importante verificar algunas métricas para constatar que el entrenamiento progrese como esperamos: que no tengamos una convergencia temprana, ni dominio del discriminador o del generador. Es es que la pérdida de alguno de ellos no se haga muy pequeña.

Lo deseable es que la perplejidad (confusión) del discriminador sea del 50%. Ésto es, que en promedio las probabilidades de la verasidad en el discriminador sea: $\mathbb{E} \left\{ -log \, \hat z_i \right\} = \log(2) = 0.693$ . Esta es una buena medida para los términos de costo del generador y discriminador.

Verfiquemos durante el entrenamiento lo siguiente.

Si disc_loss<0.69 entonces el discriminador tiene un mejor desempeño que un clasificador aleatorio en pares reales y sintéticos.
Si gen_gan_loss<0.69 entonces el generador logra confundir al dicriminador las mas de las veces.
El término MAE debe ir reduciéndose.

Restablecemos el último checkpoint y probamos la red

#!ls {checkpoint_dir}

Una vez que se entrena el modelo, leemos el Nombre del archivo del último checkpoint y cargamos los pesos.

# Restoring the latest checkpoint in checkpoint_dir
chkpnt = tf.train.latest_checkpoint(checkpoint_dir)         
chkpnt = './training_checkpoints/ckpt-5' 
checkpoint.restore(chkpnt)

<tensorflow.python.training.tracking.util.CheckpointLoadStatus at 0x7f99bc40f3a0>

Probar el generador con datos de prueba


for inp, tar in test_xy.take(8):
    generate_images(generator, inp, tar)

png

Notamos que el modelo pix2pix puede efectivamente añadir textura a las imágenes base $x$ generadas con el VAE. Algunas de las imágenes texturizadas $x^\prime$ tienen una apariencia muy realista, aunque en otras se introducen distorciones.

Finalmente, guardamos los pesos del modelo para poder usarlo posteriormente.

generator.save_weights('results_p2p/generator_weights.h5')

That all