Tutorial PyTorch: Perceptron Multi-Capa (MLP)

Red Neuronal Artificial

Basado en el blog ejemplo de regresión lineal, pytorch tutorial

Mariano Rivera

agosto 2020

PyTorch es una librería de alto nivel (similar a TensorFlow) para implementar Redes Neuronales Artificiales y ha ganado mucha popularidad entre los investigadores y desarrolladores que desean tener mas control solo la ceración, y entrenamiento de la red. Por ello, incluimos en varias secciones ejemplos de redes implementadas en PyTorch.

Para implementar un Perceptrón multicapa en PyTorch, seguiremos los siguientes pasos:

Importar librerias.
Preparar el conjunto de datos. Leeremos los datos de MNIST
Crear la RNA.
Instanciar la clase Modelo
Instanciar la función de pérdidad de la red. dado que implementaremos un clasificador multiclase, la fucnión de pérdida sera la cross-entropía (entropía cruzada) y que incluye la función softmax, por lo que no la prondremos en nuestro modelo.
Instanciar el Optimizador. Usaremos como algoritmo de entrenamiento (optimización) el Descenso de Gradiente Estócastico con acelaración de Nesterov.
Entrenar el modelo.
Realizar predicción (inferencia) para medir la eficiencia.

Importar librerias

import numpy as np
import matplotlib as plt

import os
from sklearn.model_selection import train_test_split

import torch
import torch.nn as nn
import torchvision.transforms as transforms
from torch.autograd import Variable
import torchvision.datasets as datasets

torch.__version__

'1.3.1'

use_cuda = torch.cuda.is_available()
use_cuda

True

Dado que tenemos una GPU disponible, implementaremos una MLP con varias capas ocultas. Nos servirá para ilustrar:

Pasar el modelo y variables a GPU (en Keras esto es automático si contamos con un GPU y usamos Tensorflow-GPU).
Recuparar variables de espacio del GPU al espacio del CPU.
Usar varias funciones de activación, como la ahora popular ELU.

Preparar el conjunto de datos

Carga datos, los pasa a Tensor (variable de pytorch) y los normaliza usando

$image = (image - mean) / std$

mean = (0.5,)
std = (1.0,)
datapath = './data'
trans = transforms.Compose([transforms.ToTensor(), transforms.Normalize(mean, std)])

train = datasets.MNIST(root=datapath, train=True,  download=True, transform=trans)
test  = datasets.MNIST(root=datapath, train=False, download=True, transform=trans)

print('Número de datos de entrenamiento: {} \nNúmero de datos de prueba: {}'.format(len(train), len(test)))

Número de datos de entrenamiento: 60000 
Número de datos de prueba: 10000

Definimos el directorio donde los datos se localizán (o se localizarán en caso de que no estén disponibles aun, para descargarlos en tal caso usamos download=True). Los datos no son transformados al descargarse.

Cargador de Datos (data loader)

batch_size = 100
n_iters    = 80000
num_epochs = int( n_iters / (len(train) / batch_size) )

train_loader = torch.utils.data.DataLoader(dataset    = train,
                                           batch_size = batch_size,
                                           shuffle    = True)
test_loader  = torch.utils.data.DataLoader(dataset    = test,
                                           batch_size = batch_size,
                                           shuffle    = False)

Crear la RNA

La RNA se define como una clase, ANNModel en este caso.

En el constructor __init__ se definen las capas de las cuales constará el modelo, aunque no la forma en que se interconectan.

La interconección de las capas se especifica en el método forward.

Note que la capa no lineal definida por

(1)
$y = \phi(W x + b)$

se implementa en dos pasos:

La parte lineal

(2)
$z = W x + b.$

La activación no-lineal

(3)
$y = \phi(z)$

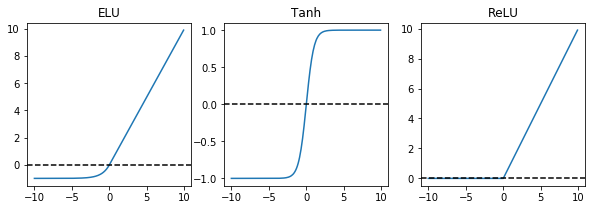
En el modelo usaremos 3 capas acultas y, para propositos de ilustración, con activaciones ReLU, Tanh y ELU.

ELU

$\text{ELU}(x) = \max(0,x) + \min(0, \alpha * (\exp(x) - 1))$

ReLU

$\text{ReLU}(x) = \max(0, x)$

import matplotlib.pyplot as plt
import numpy as np

def miReLU(x, alpha=1.):
    return x*(x>0)

def miELU(x, alpha=1.):
    y = alpha*(np.exp(x)-1)
    return x*(x>0) + y*(y<0)
   
x = np.array(range(-100,100))/10.

yReLU = miReLU(x)
yELU  = miELU(x)
yTanh = np.tanh(x)

plt.figure(figsize=(10,3))
plt.subplot(131)
plt.plot(x, yELU)
plt.axhline(0, linestyle='--', color='k')
plt.title('ELU')

plt.subplot(132)
plt.plot(x, yTanh)
plt.axhline(0, linestyle='--', color='k')
plt.title('Tanh')

plt.subplot(133)
plt.plot(x, yReLU)
plt.axhline(0, linestyle='--', color='k')
plt.title('ReLU')

plt.show()

png

Clase MLPnet

Aqui definimos la red neuronal que usaremos, sera un Perceptrón Multi-Capa (MLP):

En el método constructor __init__ definimos los componentes de nuestro MLP, note que la cala Linearno incluye la función de activación, por lo que ésta debe aplicarse como una capa extra. Por claridad, hemos definido las capas en el order que se usaran en nuestro modelo secuancial, pero esto no es obligatorio
El método forward define el la secuancia de cálculos desde la entrada hasta la salida que realiza el MPL.
En método backwarddefini los cálculos de la retropagación requeridos desde la salida hacia cada variable respecto a la cual se entrena la red. Si todos las capas componentes en forward son diferenciables (tienen su propio metodo backward, entonces el backward se define automáticamente por la secuencia inversa de los backwardde cada capa segun se invocaron en forward.

Si deseamos crear una nueva capa o función de activación debemos crear una clase con los 'metodos: __init__, forwardy backward. Todas las capas de PyTorch inlcuyen ya esos métodos,. Pero es importante tenerlo en cuenta para implementar nustroas pripoas capas (custom layer).

En nuetro MLP no uinlcuimos una función de actiovación softmax a la salida porque emplearemos como función de pérdida la CrossEntropyLoss() que ya incluye la activación softmax. Esto no es igual en Keras, donde explicitamente requerimos poner la activación softmax a la salida de una red clasificadora multiclase.

class MLPnet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(MLPnet, self).__init__()
        '''
        El método init define las capas de las cuales constará el modelo, 
        aunque no la forma en que se interconectan
        '''
        # Función lineal 1: 784 --> 100
        self.fc1 = nn.Linear(input_dim, hidden_dim) 
        # Activación no lineal 1: 100 -->100
        self.relu1 = nn.ReLU()
        
        # Función lineal 2: 100 --> 100
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        # Activación no lineal 1: 100 -->100
        self.tanh2 = nn.Tanh()
        
        # Función lineal 3: 100 --> 100
        self.fc3 = nn.Linear(hidden_dim, hidden_dim)
        # Activación no lineal 3: 100 -->100
        self.elu3 = nn.ELU()
        
        # Función lineal 3: (Capa de salida): 100 --> 10
        self.fc4 = nn.Linear(hidden_dim, output_dim)  

    def forward(self, x):
        x = x.view(-1, input_dim)  # aqui convertimos la imagen a un vector unidimensional
        # Capa 1
        z1 = self.fc1(x)
        y1 = self.relu1(z1)
        # Capa 2
        z2 = self.fc2(y1)
        y2 = self.tanh2(z2)
        # Capa 3
        z3 = self.fc3(y2)
        y4 = self.elu3(z3)
        # Capa 4 (salida)
        out = self.fc4(y4)
        return out
    
    def name(self):
        return "MLP"

Crear instancia (modelo) de la clase RNA

input_dim  = 28*28  # 784 número de pixeles
hidden_dim = 150    # número de neuronas en las capas ocultas
output_dim = 10     # número de etiquetas

model = MLPnet(input_dim, hidden_dim, output_dim)

En caso de que dispongamos de un GPU, pasamos el modelo al espacio de cálculo de la GPU.

if use_cuda:
    model = model.cuda()

Crear instancia de la función de pérdida

Dado que es clasificacion usamos la entropía cruzada

error = nn.CrossEntropyLoss()

Crear instancia del Optimizador

Usamos Descenso de gradiente estocástico (Stochastic Gradient Descent, SGD).

learning_rate = 0.02
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

Entrenar el modelo

Entrenar la red model minimizando la función de pérdida error con el optimizador optimizer

loss_list         = []
iteration_list    = []
accuracy_list     = []
accuracy_list_val = []

for epoch in range(num_epochs):
    total=0
    correct=0
    # - - - - - - - - - - - - - - - 
    # Entrena la Red en lotes cada época
    # - - - - - - - - - - - - - - - 
    for i, (images, labels) in enumerate(train_loader):
        
        if use_cuda:                              # Define variables
            images, labels = images.cuda(), labels.cuda()
        images = Variable(images) 
        labels = Variable(labels)
        
        optimizer.zero_grad()                      # Borra gradiente
        outputs = model(images)                    # Propagación
        loss    = error(outputs, labels)           # Calcula error
        loss.backward()                            # Retropropaga error
        optimizer.step()                           # Actualiza parámetros
        
        predicted = torch.max(outputs.data, 1)[1]  # etiqueta predicha (WTA)
        total += len(labels)                       # número total de etiquetas en lote
        correct += (predicted == labels).sum()     # número de predicciones correctas
        
    # calcula el desempeño en entrenamiento: Precisión (accuracy)
    accuracy = float(correct) / float(total)
    # almacena la evaluación de desempeño
    iteration_list.append(epoch)
    loss_list.append(loss.item())
    accuracy_list.append(accuracy)

    # - - - - - - - - - - - - - - - 
    # Evalúa la predicción en lotes cada época
    # - - - - - - - - - - - - - - - 
    correct = 0
    total   = 0
    for images, labels in test_loader: 


        if use_cuda:
            images, labels = images.cuda(), labels.cuda()
        images = Variable(images)                   # Define variables
        labels = Variable(labels)
        
        outputs = model(images)                     # inferencia

        predicted = torch.max(outputs.data, 1)[1]   # etiqueta predicha (WTA)  
        total += len(labels)                        # número total de etiquetas en lote
        correct += (predicted == labels).sum()      # número de predicciones correctas

    # calcula el desempeño: Precisión (accuracy)
    accuracy_val = float(correct) / float(total)
    accuracy_list_val.append(accuracy_val)

    # - - - - - - - - - - - - - - - 
    # Despliega evaluación
    # - - - - - - - - - - - - - - - 
    print('Epoch: {:02}  Loss: {:.6f}  Accuracy: {:.6f}  Accuracy Val: {:.6f}'.format(epoch, loss.data, accuracy, accuracy_val))

Epoch: 00  Loss: 0.648598  Accuracy: 0.545467  Accuracy Val: 0.811200
Epoch: 01  Loss: 0.392635  Accuracy: 0.858867  Accuracy Val: 0.885400
Epoch: 02  Loss: 0.367481  Accuracy: 0.894383  Accuracy Val: 0.904100
Epoch: 03  Loss: 0.439114  Accuracy: 0.907967  Accuracy Val: 0.916200
...
Epoch: 131  Loss: 0.000622  Accuracy: 1.000000  Accuracy Val: 0.978500
Epoch: 132  Loss: 0.000812  Accuracy: 1.000000  Accuracy Val: 0.978400

Visualización

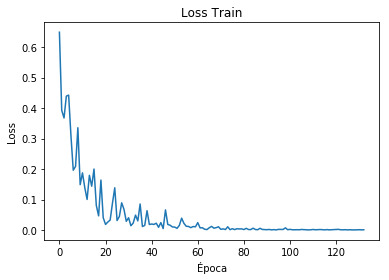
# Loss
plt.plot(iteration_list,loss_list)
plt.xlabel("Época")
plt.ylabel("Loss")
plt.title("Loss Train")
plt.show()

png

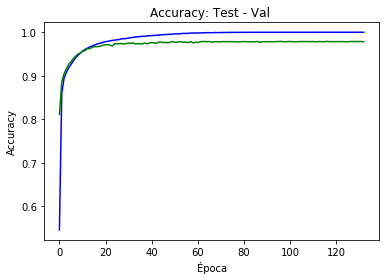
# Accuracy
plt.plot(iteration_list,accuracy_list,'b')
plt.plot(iteration_list,accuracy_list_val, 'g')
plt.xlabel("Época")
plt.ylabel("Accuracy")
plt.title("Accuracy: Test - Val ")
plt.show()

png