Perceptrón Multicapa en Tensorflow-Keras

Mariano Rivera

versión 1.1 septiembre 2023

Previas: 1.0 agosto 2020

Aprendizaje Automático, Mariano Rivera, CIMAT © 2022

---

Nuestro primer ejercicio con Keras es construir un clasificador multiclase basado en una Red Neuronal Artificial (ANN, o simplemente NN).

El objetivo es clasificar las imágenes de dígitos (28x28 pixeles) de la popular base de datos MNIST.

import numpy as np
import matplotlib.pyplot as plt

Importando Keras

import tensorflow.keras as keras
print('backend :', keras.backend.backend())
print('keras version :', keras.__version__)

backend : tensorflow
keras version : 2.9.0

Ok, estamos usando Tensorflow 2+ y keras será la API que usaremos para implementar la red neuronal.

Si queremos saber si usaremos el CPU o un el GPU como dispositivo de cómputo, necesitamos comprobarlo a través de tensorflow:

from tensorflow.python.client import device_lib
print(device_lib.list_local_devices())

[name: "/device:CPU:0"
device_type: "CPU"
memory_limit: 268435456
locality {
}
incarnation: 728060542527599681
xla_global_id: -1
]

La estación de trabajo (workstation) donde se ejecutó esta instrucción cuenta con dos dispositivos en los que se puede ejecutar tensorflow:

• el CPU, y
• un GPU (una tarjeta NVIDIA 3090 RTX).

En caso de contar con acceso a una GPU, tensorflow-gpu automáticamente se elegirá la GPU.

Cargando Datos MNIST mediante Keras

MNIST es una de las base de datos de prueba disponibles a través de Keras.

# cargar la interfaz a la base de datos que vienen con keras
from tensorflow.keras.datasets import mnist

# lectura de los datos
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

A = train_images[0]  # la primera imagen

print('Dimensiones del conjunto de entrenamiento: ', train_images.shape)
print('Dimensiones del conjunto de evaluación: ',    train_images.shape)

num_data, nrows, ncols = train_images.shape

Dimensiones del conjunto de entrenamiento:  (60000, 28, 28)
Dimensiones del conjunto de evaluación:  (60000, 28, 28)

La BD MNIST consta de 60 mil datos datos de entrenamiento y 60 mil de prueba, con sus respectivas etiquetas.

La datos para cada clase estan aproximadamentre balanceados: cerca de 6 mil para imágenes para cada clase.

plt.figure(figsize=(10,10))
plt.subplot(211)
plt.hist(train_labels[:], bins=10)
plt. title('Conteo de las etiquetas del conjunto de entrenamiento')
plt.subplot(212)
plt.hist(test_labels[:], bins=10)
plt. title('Conteo de las etiquetas del conjunto de prueba')
plt.show()

Ejemplos de las imágenes para cada clase

plt.figure(figsize=(10,4))

for i in range(10):
    plt.subplot(2,5,i+1)
    idx = list(train_labels).index(i)
    plt.imshow(train_images[idx], 'gray')
    plt.title(train_labels[idx])
    plt.axis('off')
    
plt.show()

A continuación desplegamos las primeras 400’s ocurrencias de las imágenes de los dígitos 1 y 7.

nrowsIm = 20
ncolsIm = 20
numIm = nrowsIm*ncolsIm

digit=1
Indexes = np.where(train_labels==digit)[0][:numIm]

plt.figure(figsize=(12,12))
for i,idx in enumerate(Indexes[:numIm]):
    plt.subplot(nrowsIm,ncolsIm,i+1)
    plt.imshow(train_images[idx], 'gray')
    plt.axis('off')
    
plt.show()

digit=7
Indexes = np.where(train_labels==digit)[0][:numIm]

plt.figure(figsize=(12,12))
for i,idx in enumerate(Indexes[:numIm]):
    plt.subplot(nrowsIm,ncolsIm,i+1)
    plt.imshow(train_images[idx])
    plt.axis('off')
    
plt.show()

Preprocesamiento de los Datos

Usaremos una red clasificadora que usa vectores de entrada unidimensionales (tensores de orden 1). Por lo que preprocesamos cada imagen para:

1. Transformarla de un tensor de orden 3 de $28 \times 28 \times 1$ (pixeles por renglón, pixeles por columna, número de canales) a un tensor unimensional de $784$ entradas.

2. Normalizar en valores de cada entrada al intervalo $[0, 255]$.

train_images = train_images.reshape((60000, -1))
train_images = train_images.astype('float32') / 255

test_images  = test_images.reshape((10000, -1))
test_images  = test_images.astype('float32') / 255

numIm, szIm  = train_images.shape

Además, las etiquetas, originalmente codificadas en un entero en el conjunto $\{0,1,2,\ldots,9\}$, las transformaremos a un vector de la base canónica $e \in \{ e_i\}_{i=1,2,\ldots,10}$:

Por ejemplo, la etiqueta $y=5$, es mapeada al vector

En al argot de redes neuronales, a esta codificación se denomina one-hot, vectores indicadores (generalmente), o variables categóricas.

Con Keras este mapeo se realiza mediante el siguiente código.

from tensorflow.keras.utils import to_categorical

train_labels = to_categorical(train_labels)
test_labels  = to_categorical(test_labels)

Arquitectura de la red de Percetrones Multicapa

Lo primero que hacemos es definir el tipo de modelo red que usaremos.

El modelo más popular de NN para implementar clasificadores es el Secuencial. En una red secuencial los datos se alimentan a la primera capa oculta y son procesador capa por capa (hacia adelante) hasta la capa de salida, la cual tienen como salida el vector deseado.

En nuestro caso, el vector deseado será de tamaño 10 (como las etiquetas codificadas en one-hot) pero tomarán valores en el intervalo $[0,1]$ y la suma de la salida para un dato dato deberá sumar 1. De ésta manera la salida de la red la interpretaremos como la probabilidad de que el dato pertenezca a cada clase.

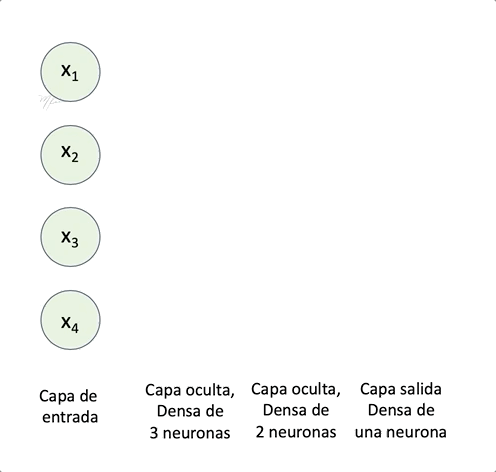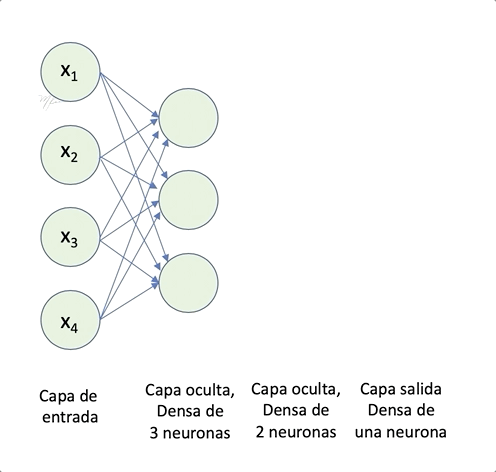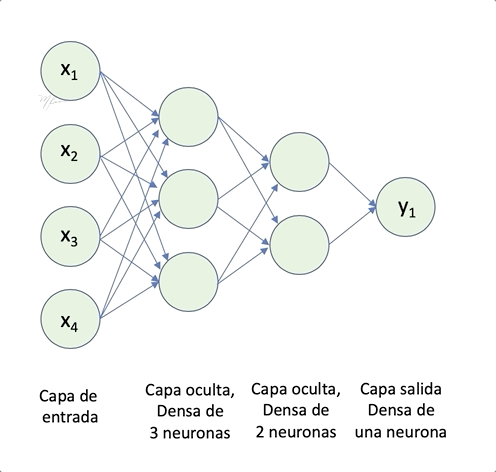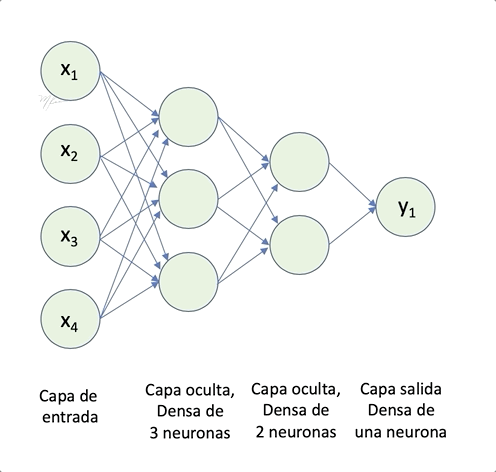
La arquitectura de nuestra red secuencial consistirá en tres capas ocultas densamente conectadas: cada neurona en una capa se conecta con todas la salidas de cada neurona de la capa anterior.

Existen distintos tipos de capas en una red secuencial.

• Las capas Dense son la capas de cálculo de que conectan cada neurona en una capa con todas las salidas de la capa anterior.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

model = Sequential()            # Modelo secuencial 

• capa de entrada: Son las neuronas que representan los datos de entrada, no es necesario definir esta capa en Keras. Lo que requerimos es especificar las dimensiones de los datos en la primera capa oculta.

• primera oculta: Los parámetros mínimos son el número de neuronas (units), la función de activación y la dimensión de los datos de entrada (1D).

• capas ocultas intermendias: Los parámetros mínimos son el número de neuronas (units) y la función de activación. La dimensión de los datos de entrada corresponde al número de neuronas en la capa anterior.

• capa de salida: Capa con la respuesta codificada, tendremos tantas neuronas como clases (10 en el caso de clasificación de imágenes de dígitos de la DB MNIST). Cada salida la intepretaremos como la probabilidad de que el dato de entrada pertenezca a dicha clase. Consecuentemente, usaremos softmax como función de activación.

La siguiente figura muestra un esquema de la red secuencial. La que proponemos implementar tendrá menos capas.

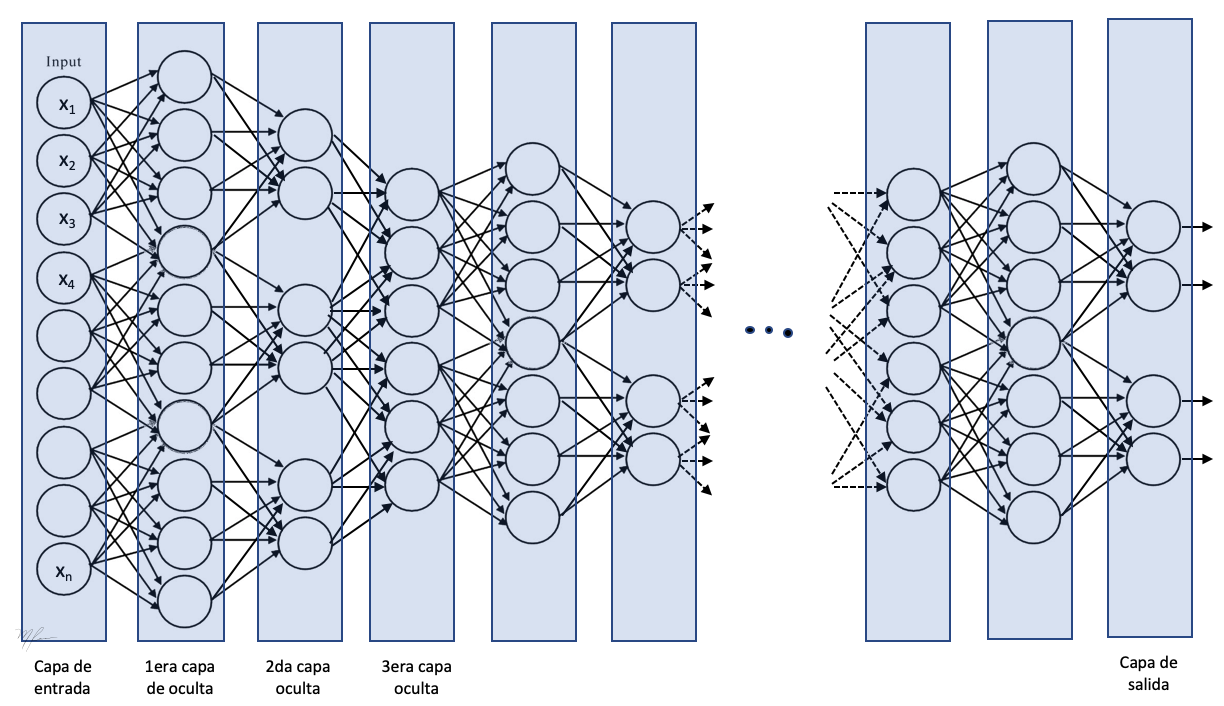
Parámetros de una capa Densa (Dense)

Algunos de los parámetros mas importantes son:

• units: Número de neuronas (entero positivo), es la dimensión de la salida y, por ende, de entrada de la siguiente capa.

• input_shape: Dimensión (entero positivo) de los datos de entrada a cada capa, solo es neceasario especificarlo en la primera capa de procesamiento de la red [input_shape=(szIm,)] dejando sin definir las dimensiones del lote (batch) a procesar. Para las demás capas, el tamaño del vector de entrada se define automáticamente por el número de neuronas en la capa anterior.

• use_bias: {True, False}, si las neuronas de la capa tienen usan sesgo (bias).

• kernel_initializer: Inicializadores de la matriz de pesos de la capa; ver initializers.

• bias_initializer: Innializador del vector de sesgos (bias).

• kernel_regularizer: Función de regularización aplicada a los pesos (L1, L2, L1+L2); ver regularizer.

• bias_regularizer: Función de regularización aplicada al vector bias.

• activity_regularizer: Función de regularización aplicada a las salidas de la capa.

• kernel_constraint: Función de restricción aplicada a los pesos de la capa (matriz de pesos); ver constraints.

• bias_constraint: Función de restricción aplicada al vector bias.

• activation: Función de activación default, activación lineal: $\phi(x)$ = x). A continuación ilustramos funciones de activación comunes, la softmax se ilustra sin normalizar.

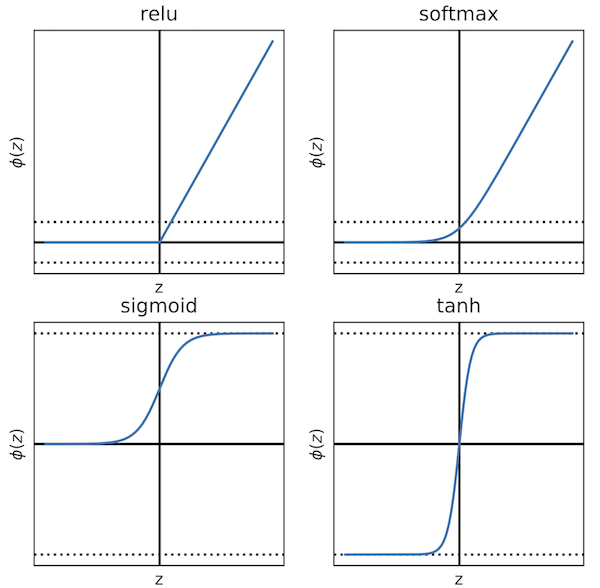
'linear' (default):
$$\phi(y) = y$$

'relu' (rectified linear unit):
$$\phi(y) = \max\{ 0,y\}$$

'softmax' (salidas normalizada a suma 1):
$$\phi(y)_i = \frac{\exp(y_i)}{\sum_k \exp(y_k)}$$

'sigmoid' :
$$\phi(y) = \frac{1}{1+ \exp(-y)}$$

'tanh' :
$$\phi(y) = \tanh(y)$$

'None' : sin función de activación.

Definir la función de activación como None nos permite introducir un procesamiento (otra capa + layer) antes de invocar a la activación específica. Para cargar una capa de activación podemos usar

import tensorflow.nn as nn
from tensorflow.keras.layers import Activation
# y en su momento usar, por ejemplo'
Activation('relu')
# o
Activation(nn.relu)

(código de ilustración, no se ejecute)

Ahora si, definamos la arquitectura de nuestra red neuronal densa. Para ello usamos keras en su versión mas simple. Al modelo que hemos definido como secuencial agregamos capa tras capa. Recordemos que sólo es necesario definir las dimensiones de los datos de entrada para la primara capa y Keras hará el resto por nosotros.

# añadir al modelo nn la primera capa oculta
model.add(Dense(units             = 512,          # número de neuronas en la capa 
                       activation ='relu',        # función de activacion: lineal-rectificada
                       input_shape= (szIm,)))     # forma de la entrada: (szIm, ) la otra 
                                                  # dimensión es el tamaño de lote (szBatch), 
                                                  # que se define en 'fit'
# añadir capa de salida
model.add(Dense(units             = 10, 
                activation        = 'softmax'))   # función de activación: softmax

Ahora podemos visualizar el resumen de la arquitectura

Nombre de la capa (Tipo) – Forma del vector de salida – Número de parámetros

model.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 512)               401920    
                                                                 
 dense_1 (Dense)             (None, 10)                5130      
                                                                 
=================================================================
Total params: 407,050
Trainable params: 407,050
Non-trainable params: 0
_________________________________________________________________

Como vemos, la red model tienen en total 407,050 parámetros (pesos), y todos parámetros son entrenables: no hay parámetros fijos.

Selección de los parámetros del entrenamiento (training)

Antes de pasar al proceso de entrenamiento de la red, es necesario definir lor parámetros de entrenamiento mediante el método compile que tienen los siguientes parámetros:

optimizer: método de optimización, por ejemplo: gradiente estocástico (sgd), rmsprop, adagrad, adam, adamax, nadam, etc.

loss (función de pérdida): Función abjetivo a minimizar. Médida disimilaridad entre el valor deseado (etiquetas de entrenamiento y el valor predicho por la red). Para el caso de probabilidades de variables categóricas es recomendable usar la cross-entropía categórica (categorical_crossentropy). Para el caso de clasificación binaria, la cross-entropía binaria (binary_crossentropy) es una función objetivo mas apropiada. Otras funciones de pérdida incluyen a la Error Cuadrático Medio (mse); el Error Absoluto Medio(mae); suma de log-cosh, etc.

metrics: Lista de métricas a monitorear durante el proceso de entrenamiento. Una métrica a monitorear siempre adecuada es ‘accuracy’. Además, es posible incluir métricas definidas por el usuario.

El método compile cambia únicamete los parámetros del entrenamiento y no modifica en nada los párametros de la red. Esto es, en una red preenetrenada no altera los pesos. De igual forma si se compila-entrena un modelo por un número dado de iteraciones (veremos el concepto de época al ver el método para entrenar fit), y luego modificamos los parámetros de entrenamiento con compile y volvemos a entrenar, el segundo entrenamiento retomará el proceso donde el primer entrenamiento se quedó.

model.compile(optimizer = 'rmsprop',
              loss      = 'categorical_crossentropy',
              metrics   = ['accuracy'])

Selección del algortimo de optimización

Podemos seleccionar el algoritmo de optimización específico y ajustar sus parámetros. Por ejemplo, si en vez de usar rmsprop en el caso anterio, usamos Descenso de Gradente Estocástico (SGD) tipo Nesterov, podemos usar la variante con momentum del tipo Nesterov y con decaimiento del factor de aprendizaje después de cada actualización de lote (batch); en este caso podemos usar:

from tensorflow.keras import optimizers
# parámetros de mátodo de optimización
sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)

# parámetros del procedimiento de aprendizaje (incluye que optimizador usar)
other_model.compile(loss='mean_squared_error',  optimizer=sgd)

(código de ilustración, no se ejecute)

Entrenamiento (training)

Para realizar el entrenamiento se invoca a la función fit que recibe parámetros sobre como los datos son empleados

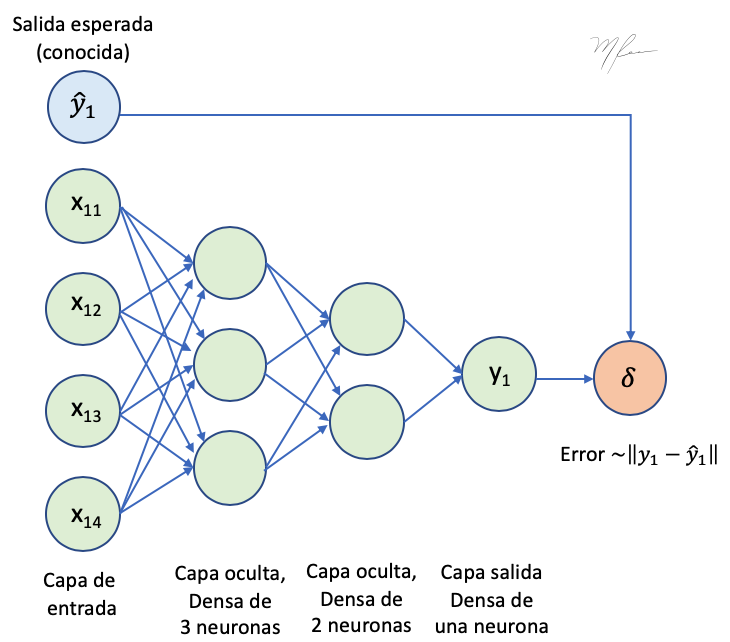
Recordemos que el propósito de la NN es estimar la función entre las entradas, $x$, y las salidas, $y$:

$$y = f(x;\theta)$$

donde $\theta$ denota los pesos de la red.

Parámetros

x: Arreglo multidimensional (numpy) con los datos de entrenamiento.

y: Arreglo (multidimensional) con las etiquetas esperadas.

batch_size: Número de muestras por cada actualización del gradiente (default, 32).

epochs: Número de veces (épocas) que el conjunto de entrenamiento es enteramente procesado (en lotes de batch_size en batch_size).

validation_split: Flotante (float) en el intervalo $[0,1]$, que representa la fracción de datos usados para validación. Los datos de validación no se usan en el entrenamiento y se usan para monitorear el progreso de la función de pérdida (loss) y las métricas (metric).

validation_data: Se puede pasar explícitamente el conjunto de validación mediante la tupla (x_val, y_val).

shuffle: Boolena (boolean) indica si los datos de entrenamiento son remezclados antes de cada época.

class_weight: Lista con pesos relativos de las clases (índices). Forza a dar mas peso a la clasificación de ciertas clases.

sample_weight: Peso relativo de los datos de entrenamiento. Útil para pasar distintamente datos de distintas clases cuando la base de datos no esta balanceda.

initial_epoch: Época para iniciar el entrenamiento (para reanudar un entrenamiento en el punto suspendido).

steps_per_epoch: Número de pasos por época. Por default es el número de datos de entrenamiento dividido entre el tamaño de los lotes

validation_steps: Sólo relevante cuando se especifica steps_per_epoch, es el número de pasos de validación antes de parar.

verbose: entero {0, 1, 2}; modo de reporte de avance, palabreo o verbosidad (verbosity): 0 = silencio, 1 = barra de progreso, 2 = linea por época.

---

También está

callbacks: Lista de funciones callback a invocarse durante el entrenamiento para monitorear los estados internos del modelo durante el entrenamiento. Es posible pasar funciones callback definidas por nosotros.

---

Regresa

History: El atributo history del objeto History regresado contiene un diccionario con los valores de la función objetivo y de las métricas a través de las distintas épocas de entrenamiento.

import time
tic=time.time()

history = model.fit(x          = train_images, 
                    y          = train_labels, 
                    validation_split=0.2,
                    epochs     = 20, 
                    shuffle    = True,
                    batch_size = 128,
                    verbose    = 2)

print('Tiempo de procesamiento (secs): ', time.time()-tic)

Epoch 1/20
375/375 - 1s - loss: 0.2915 - accuracy: 0.9166 - val_loss: 0.1534 - val_accuracy: 0.9567 - 1s/epoch - 4ms/step
Epoch 2/20
375/375 - 1s - loss: 0.1211 - accuracy: 0.9637 - val_loss: 0.1085 - val_accuracy: 0.9671 - 1s/epoch - 3ms/step
Epoch 3/20
375/375 - 2s - loss: 0.0787 - accuracy: 0.9762 - val_loss: 0.0863 - val_accuracy: 0.9751 - 2s/epoch - 5ms/step
Epoch 4/20
375/375 - 1s - loss: 0.0565 - accuracy: 0.9835 - val_loss: 0.0858 - val_accuracy: 0.9748 - 1s/epoch - 3ms/step
Epoch 5/20
375/375 - 1s - loss: 0.0426 - accuracy: 0.9873 - val_loss: 0.0801 - val_accuracy: 0.9759 - 1s/epoch - 3ms/step
Epoch 6/20
375/375 - 1s - loss: 0.0313 - accuracy: 0.9905 - val_loss: 0.0777 - val_accuracy: 0.9783 - 1s/epoch - 3ms/step
Epoch 7/20
375/375 - 1s - loss: 0.0247 - accuracy: 0.9927 - val_loss: 0.0833 - val_accuracy: 0.9764 - 1s/epoch - 3ms/step
Epoch 8/20
375/375 - 1s - loss: 0.0187 - accuracy: 0.9944 - val_loss: 0.0790 - val_accuracy: 0.9800 - 1s/epoch - 3ms/step
Epoch 9/20
375/375 - 1s - loss: 0.0140 - accuracy: 0.9962 - val_loss: 0.0887 - val_accuracy: 0.9787 - 1s/epoch - 3ms/step
Epoch 10/20
375/375 - 1s - loss: 0.0109 - accuracy: 0.9971 - val_loss: 0.0919 - val_accuracy: 0.9783 - 1s/epoch - 3ms/step
Epoch 11/20
375/375 - 1s - loss: 0.0082 - accuracy: 0.9976 - val_loss: 0.0883 - val_accuracy: 0.9797 - 1s/epoch - 3ms/step
Epoch 12/20
375/375 - 1s - loss: 0.0060 - accuracy: 0.9986 - val_loss: 0.0920 - val_accuracy: 0.9805 - 1s/epoch - 3ms/step
Epoch 13/20
375/375 - 1s - loss: 0.0047 - accuracy: 0.9986 - val_loss: 0.0938 - val_accuracy: 0.9807 - 1s/epoch - 3ms/step
Epoch 14/20
375/375 - 1s - loss: 0.0034 - accuracy: 0.9991 - val_loss: 0.1068 - val_accuracy: 0.9779 - 1s/epoch - 3ms/step
Epoch 15/20
375/375 - 1s - loss: 0.0027 - accuracy: 0.9993 - val_loss: 0.1074 - val_accuracy: 0.9790 - 1s/epoch - 3ms/step
Epoch 16/20
375/375 - 1s - loss: 0.0023 - accuracy: 0.9994 - val_loss: 0.1163 - val_accuracy: 0.9782 - 1s/epoch - 3ms/step
Epoch 17/20
375/375 - 1s - loss: 0.0015 - accuracy: 0.9996 - val_loss: 0.1142 - val_accuracy: 0.9784 - 1s/epoch - 3ms/step
Epoch 18/20
375/375 - 1s - loss: 0.0011 - accuracy: 0.9998 - val_loss: 0.1135 - val_accuracy: 0.9797 - 1s/epoch - 3ms/step
Epoch 19/20
375/375 - 1s - loss: 0.0010 - accuracy: 0.9998 - val_loss: 0.1200 - val_accuracy: 0.9792 - 1s/epoch - 3ms/step
Epoch 20/20
375/375 - 1s - loss: 8.1316e-04 - accuracy: 0.9998 - val_loss: 0.1226 - val_accuracy: 0.9796 - 1s/epoch - 3ms/step
Tiempo de procesamiento (secs):  23.398916482925415

Conjuntos de entrenamiento, validación y prueba

Podemos notar que el mejor desempeño en la función de pérdida sobre conjunto de validación lo tenemos al fin de la época 6:

• El valor de la función objetivo alcanzado es cercano a:

  • 3.13e-2 para los datos del conjunto de entrenamiento
  • 7.77e-2 para el conjunto de validación (sustancialmente mas alto, menos es mejor).

• Algo similar pasa con la métrica (accuracy):

  • 99.05% para conjunto de entrenamiento.
  • 97.83% para el conjunto de validación (mas es mejor).

Nota: lo valores pueden variar de corrida a corrida, pero serán cercanos a estos si el entrenamiento fué exitoso.

La disparidad en los valores del conjunto de entrenamiento con el de prueba se debe a que la red no utilizó los datos de validación para ajustar los pesos (nunca vió los datos de validación). El desempeño de la red en el conjunto de validación sería el desempeño esperado en datos no observados, como los de prueba.

Luego, vemos que a partir de la época 8, la red continua mejorando en las métricas sobre el conjunto de entrenamiento pero empeora en el conjunto de validación. Lo que ha ocurrido es que la red ha memorizado algunas características presentes en los datos de entrenamiento que no están presentes en los datos de validación. Estas características que hacen la diferencia son muy particulares de algunos datos y no se les puede considerar atributos del universo de datos. Este error (diferencia entre desempeño en datos no observados vs. datos con que se entrenó el clasificador) se conoce como error de generalización y se debe a un sobreentrenamiento (sobreajuste) de la red en el conjunto de entrenamiento, también denominado overfitting.

Note que aún no hemos evaluado la red en el conjunto de prueba es que nuestro diseño final debe evaluarse solo una vez en el conjunto de prueba. Las razón es:

Cada vez que modificamos algún parámetro de la red (número de capas, número de neurones an las capas, funciónes de activación, función de pérdida, etc.) con el propósito de mejorar el desempeño del modelo (NN) que estamos diseñando en el conjunto de datos de validación, actuamos, de hecho, como un optimizador de la función objetivo, y en el proceso podemos llegar a un sobreajuste de los datos de validación. Perdiendo con ello al característica del conjunto de validación de ser totalmente no observable.

Es como si en cada iteracion de nuestro proceso de diseño de la NN, parte de la informacion del conjunto de validación se fuera pasando al conjunto de entrenamiento en un proceso de fuga de información (information leak).

Para analizar como se comporta los valores de la función objetivo y de las métrica, analizamos el objeto History devuelto por el proceso de entrenamiento.

history_dict = history.history
dictkeys=list(history_dict.keys())
dictkeys

['loss', 'accuracy', 'val_loss', 'val_accuracy']

Estas son la llaves (keys) de los arreglos con los valores monitoreados.

Veamos el comportamiento del valor de la función objetivo.

loss_values     = history.history['loss']
val_loss_values = history.history['val_loss']
epochs = range(1, len(loss_values) + 1)


plt.figure(figsize=(12,5))
plt.plot(epochs, loss_values, 'b', label='Training loss')
plt.plot(epochs, val_loss_values, 'g', label='Validation loss')
plt.title('Valor de la función objetivo (loss) en conjuntos de en entrenamiento y validación')
plt.xlabel('Epocas')
plt.ylabel('')
plt.hlines(y=.078, xmin=0, xmax=20, colors='k', linestyles='dashed')
plt.legend()

plt.show()

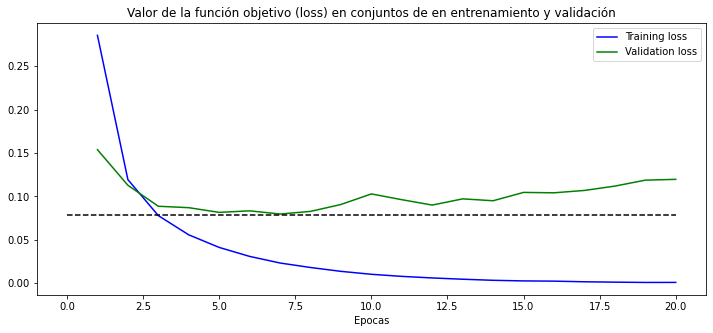
y el comportamiento del valor de la métrica monitoreada

acc_values = history_dict['accuracy']
val_acc_values = history_dict['val_accuracy']


plt.figure(figsize=(12,5))
plt.plot(epochs, acc_values, 'b', label='Accuracy')
plt.plot(epochs, val_acc_values, 'g', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.hlines(y=.982, xmin=0, xmax=20, colors='k', linestyles='dashed')
plt.legend()

plt.show()

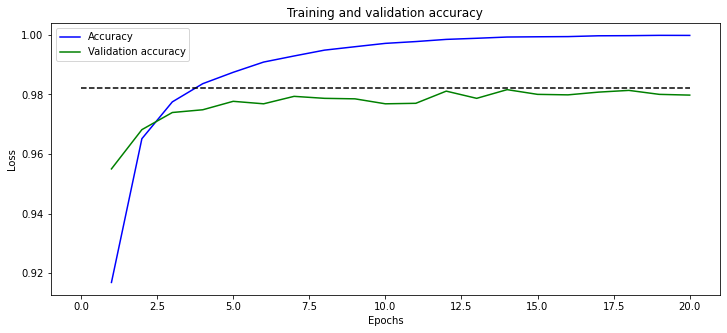
Como se puede observar, la función de pérdida en el conjunto de validación alcanza su mínimo alrededor de las épocas 5 a 8, después incrementa su valor. A ese número de épocas, el accuracy también tienen un máximo local.
Por lo que ejecutaremos el entrenamiento sólo por 6 épocas.

Diseño final

El código completo y final del clasificador de red perceptrón multicapa es el de a continuación.

# cargar la interfaz a la base de datos que vienen con keras
from tensorflow.keras.datasets import mnist

# lectura de los datos
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

# prepocesamiento de los datos
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255

test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

numIm, szIm = train_images.shape

from tensorflow.keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels  = to_categorical(test_labels)

# Arquitectura de la red
from tensorflow.keras import models
from tensorflow.keras import layers
import time

model = models.Sequential()    
model.add(layers.Dense(units=512,activation='relu', input_shape=(szIm,)))         
model.add(layers.Dense(units=10, activation='softmax'))

model.compile(optimizer='rmsprop',
              loss     ='categorical_crossentropy',
              metrics  =['accuracy'])

tic=time.time()
history = model.fit(x          = train_images, 
                    y          = train_labels, 
                    validation_split=0.2,
                    epochs     = 8, 
                    shuffle    = True,
                    batch_size = 128,
                    verbose    =2)
print('Tiempo: {} secs'.format(time.time()-tic))

Epoch 1/8
375/375 - 1s - loss: 0.2896 - accuracy: 0.9160 - val_loss: 0.1389 - val_accuracy: 0.9596 - 1s/epoch - 4ms/step
Epoch 2/8
375/375 - 1s - loss: 0.1191 - accuracy: 0.9644 - val_loss: 0.1023 - val_accuracy: 0.9697 - 1s/epoch - 3ms/step
Epoch 3/8
375/375 - 1s - loss: 0.0783 - accuracy: 0.9770 - val_loss: 0.0916 - val_accuracy: 0.9734 - 1s/epoch - 3ms/step
Epoch 4/8
375/375 - 1s - loss: 0.0562 - accuracy: 0.9835 - val_loss: 0.0747 - val_accuracy: 0.9775 - 1s/epoch - 3ms/step
Epoch 5/8
375/375 - 1s - loss: 0.0409 - accuracy: 0.9879 - val_loss: 0.0829 - val_accuracy: 0.9750 - 1s/epoch - 3ms/step
Epoch 6/8
375/375 - 1s - loss: 0.0313 - accuracy: 0.9909 - val_loss: 0.0756 - val_accuracy: 0.9789 - 1s/epoch - 3ms/step
Epoch 7/8
375/375 - 1s - loss: 0.0239 - accuracy: 0.9932 - val_loss: 0.0868 - val_accuracy: 0.9774 - 1s/epoch - 3ms/step
Epoch 8/8
375/375 - 1s - loss: 0.0179 - accuracy: 0.9953 - val_loss: 0.0773 - val_accuracy: 0.9802 - 1s/epoch - 3ms/step
Tiempo: 9.18740725517273 secs

results = model.evaluate(test_images, test_labels)
print(results)

313/313 [==============================] - 0s 624us/step - loss: 0.0986 - accuracy: 0.9816
[0.09860528260469437, 0.9815999865531921]

Como podemos notar el accuracy en test es 99.53%. Ésto es consistente con un bue desemeño de la misma métrica en el conjunto de validación.

Visualización del desempeño

Ahora que ya tenemos nuestro modelo final, podemos evaluar el mismo es el conjueto de entrenamiento. Para ello llamamos el método ‘predict’ de nuestro modelo.

y_pred = model.predict(test_images).squeeze()

score = model.evaluate(test_images, test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

313/313 [==============================] - 0s 577us/step
Test loss: 0.07187686860561371
Test accuracy: 0.9793000221252441

import numpy as np
# Import the modules from sklearn.metrics
from sklearn.metrics import confusion_matrix, precision_score, recall_score, f1_score, cohen_kappa_score

y_test_label = np.argmax(test_labels,1) 
y_pred_label = np.argmax(y_pred,1)

Matriz de Confusión

Los renglones corresponden a las etiquetas reales y las columnas a las predichas.

C=confusion_matrix(y_pred_label, y_test_label)
print(C)

[[ 972    0    3    0    2    4    5    2    2    4]
 [   0 1129    1    0    0    0    2    4    0    2]
 [   1    2 1008    3    4    0    2   10    2    0]
 [   1    0    3  996    0   16    1    6    8    6]
 [   1    0    1    0  959    1    4    0    4    7]
 [   0    1    0    0    0  861    6    0    2    2]
 [   1    2    2    0    2    3  938    0    0    0]
 [   1    0    6    2    2    0    0  995    2    2]
 [   3    1    8    3    1    4    0    2  949    0]
 [   0    0    0    6   12    3    0    9    5  986]]

Asi que de 983 imágenes con correspondientes al dígito 0, 972 fueron efectivamente clasificados como 0, ninguna como 1, tres como 2, tres como 3, y asi; finalmente cuatro como 9.

La matriz de confusion C se puede mostrar como imágen, codificando en color las coocurrencias. Como la gran mayoría de los digitos son correctamente clasificados, solo veriamos una diagonal dominante y poca diferencia fuera de la misma. Por ello, mejor desplegamos el logaritmo de C+1 (el uno para evitar la indefinición del logaritmo de cero).

import matplotlib.pyplot as plt
import seaborn as sns
# En escala logaritmica !
plt.figure(figsize=(8,6.5))
plt.title('matriz de Confusion (escala log)')
sns.heatmap(np.log(C+1), 
            xticklabels=np.arange(10), 
            yticklabels=np.arange(10),
            square=True,
            linewidth=0.5,)

plt.show()

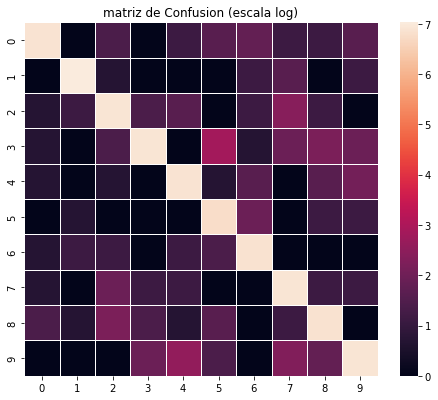
Ahora es mas fácil detectar las confusiones

Métricas de Desempeño

Si vamos a clasificar datos en $n$ clases, podemos fijarnos en una clase en particular y considerar los datos de prueba en dos categorias: los que pertenecen a la clase en que nos estamos fijando y aquellos que no. Como en el esquema lado derecho del la siguiente figura.

Ahora, dependiendo del resultado del clasificador, cada dato evaluado puede caer en alguna de las siguientes cuatro categorías:

• Verdaderos positivos (tp). Los que pertenecian a la clase y fueron correctamente clasificados en dicha clase

• Verdadero negativos (tn). Los que no pertenecian a la clase y fueron correctamente clasificados como de otra clase (sin importarnos si esa otra clase esta correcta, basta que no esté en la clase que nos interesa).

• Falsos positivos (fp). Los que no pertenecian a la clase y fueron equivocadamente asignados a la clase.

• Falsos negativos (fn). Los que pertinecian a la clase y fueron equivocadamente clasificados en otra clase.

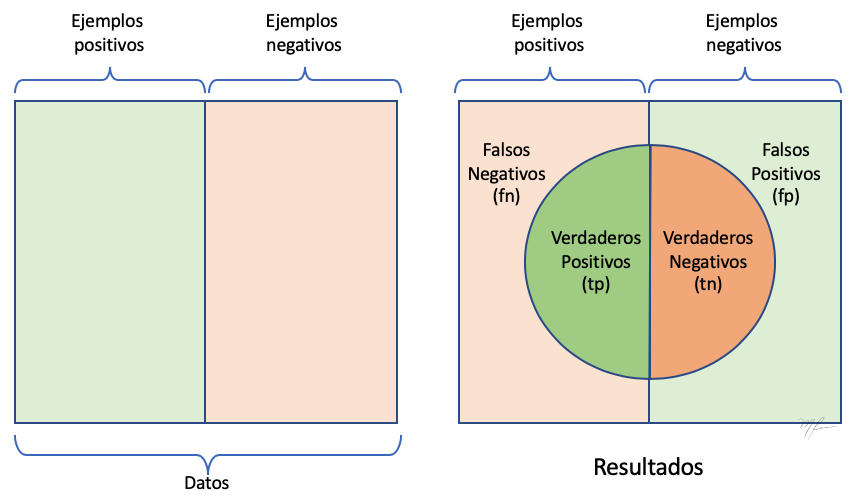
La importancia de definir estos cuatro tipos de resultados respecto, a solo indicar si es correcta o incorrecta la clasificación, es que generalmente los errores no son igual de relevantes si son falsos negativos o falsos positivos.

Considere una prueba de detección de alguna enfermedad, un falso positivo es entregar un resultados de padecer la enfermedad a un paciente que no lo tiene. En este caso, lo que generalmente se hace es hacer una segunda prueba, más exacta aunque más costosa, que corregirá el primer diagnóstico. Si bien, hubo un estrés inecesario para el pasiente y un costo por la segunda prueba, esto es preferible a cometer errores del tipo falsos negativos: diagnosticar a alguién sano cuando efectivamente padece la enfermedad y no se le suministre ningún tratamiento.

Basados en estos cuatro tipos de resultados (tp, tn, fp, y fn), se definen las siguientes métricas.

Exactitud (accuracy)

Porcentaje de datos clasificados correctamente

$$A = \frac{tp+tn}{tp+tn+fp+fn}$$

Precisión

Fracción de datos correctos entre los datos detectados como “Positivos”.

$$P = \frac{tp}{tp+fp}$$

Precisión es la probabilidad de que un dato selecionado aleatoriamente sea relevante

precision_score(y_pred_label, y_test_label, average='macro')

0.9789818047616603

Recall (sensibilidad)

Fracción de los datos positivos que han sido detectados como positivos

$$R = \frac{tp}{tp+fn}$$

Recall es la probabilidad de que un dato relevante sea selecionado aleatoriamente.

# Recall
recall_score(y_pred_label, y_test_label,  average='macro')

0.9793790045809786

Especificidad

$$R = \frac{tn}{tn+fp}$$

F1-score

$$F_1 = \frac{2}{\frac{1}{P}+ \frac{1}{R} } = \frac{2 \,P \, R} {P+R}$$
Media armónica de la precisión y el recall. Penaliza el desbalance entre las métricas P y R

f1_score(y_pred_label, y_test_label,  average='macro')

0.9791312027547278

Coeficiente kappa de Cohen

cohen_kappa_score(y_pred_label, y_test_label)

0.9769903387545689

Excelente!