Representación Implícita con Capas SIREN

Versión simplificada de la oficial en SIREN

Mariano Rivera

version 1.0, diciembre 2022.

Representación implícita

Estamos acostumbrado a representar señales e imágenes a través de vectores y matrices; respectivamente. Estas representaciones discretas son muestras de señales reales de mundo que de forma natural son continuas. representar en forma discreta estos datos tiene ventajas inheretes para su almacenamiento, procesamiento, y transmición a través de computadoras de naturaleza digital. Al mismo tiempo, al ser muestras de señales reales si se viola el criterio e Nyquist se tiene pérdida de información y falseamiento de la misma (aliasing).

En esta notas se presenta como usar la librería PyTorch para optimizar funciones de costo cuyos parámetros son directamente las variables que buscamos (imágenes); ver MRF. Ahora consideremos otro enfoque, asumamos que en vez de representar explícitamente la solución a nuestro problema, ésta se representa mediante una red neuronal. Es decir, asumimos que existe una función $f$ que realiza el mapeo:

(1)
$f: x \mapsto y$
donde $x$ es la variable independiente y $y$ la dependiente. Por ejemplo, considere una imagen en tonos de gris $I$ , cuyas posiciones de pixeles están dados por $\{ x_i\}_{i=1,2,3, \ldots, N}$ con $N = m \times n$ , y $(m,n)$ son las dimensiones de la imagen.

Luego, a cada posición $x_i$ le corresponde un valor de gris $y_i \in [0, 255]$ .

Ahora, podemos ver cada par $(x_i, y_i)$ como una dato para entrenar nuestro modelo $\Phi_\theta$ (parametrizado por $\theta$ ) que aproxima a la función verdadera $f$ . Luego tenemos varias opciones para elegir el modelo $\Phi_\theta$ las primeras que se nos pueden ocurrir en froma natural son las Funciones Base Radial (RBFs) y, por supuesto el Perceptrón Multicapa (MLP); ambos son aproximadores universales de funciones.

Aquí analizaremos el caso del MLP, en el cual usamos los pares $(x_i, y_i)$ para entrenar el MLP. Recordemos que un MLP de una capa oculta corresponde a:

(2)
$z = \phi_1(W_1 x + b_1) \\ \hat y = \phi_2(W_2 z + b_2)$
donde $\hat y$ es la predicción de $y$ , $\theta = (W_1, b_1, W_2, b_2)$ son los parámetros del modelo y $(\phi_1, \phi_2)$ son las funciones de activación; generalmente $\tanh$ o ReLU. Entonces para aprender los parámetros $\theta$ definimos una función de pérdida, digamos

(3)
$L(\theta; x, y) = \sum_{i \in \Omega} \| y_i - \hat y_i(\theta) \|$

y la optimizamos usando descenso estocástico seleccionando en cada iteración un subconjunto de los pixeles $\Omega$ (batch) usando como gradiente

(4)
$g = \nabla_\theta \sum_{i \in \Omega} \| y_i - \hat y_i(\theta) \|.$

Para entrenar la red de representación implícita se se procede a sobreentrenar (overfit) el model.

Capa SIREN

Antes de pasar revisar otras posibles aplicaciones de la representación implícita, introduciremos una capa que ha mostrado tener propiedades interesantes en cuanto a estabilidad para su entrenamiento. Esta capa es denominada SIREN y toma su nombre de Periodic Activation Implicit Neural Representations (Sitzmann et al., 2020). Esta capa corresponde a una capa densa pero con activación senoidal:

(5)
$\mathrm{siren}(x; \omega, W, b) = \sin(\omega \,(W x + b) )$
donde $\omega$ es un factor de escala no entrenable. Los autores proponen usar $\omega=30$ para datos de $256 \times 256$ , y los parámetros se inicialializan acorde a

(6)
$W_1, b_1 \sim U \left( \left[ -\frac{1}{n}, \; \frac{1}{n} \right] \right)$
para la primera capa y

(7)
$W_i, b_i \sim U \left( \left[-\frac{1}{30} \sqrt{\frac{6}{n}}, \; \frac{1}{30} \sqrt{\frac{6}{n}} \right] \right)$
para las subsecuentes capas; donde $n$ es la dimensión del vector de entrada $x$ a la capa. En PyTorch los pesos son inicializados por omisión a $U \left( \left[ -\sqrt{ 1/ n}, \; \sqrt{1 / n} \right] \right)$ . En esta implementación usamos la inicialización por omisión de PyTorch para la primera etapa, dado que de acuerdo a nuestros experimentos produjo mejores resultados.

La intención de usar activación periódica senoidal es que $\sin(t) \approx t$ para $t$ 's pequeñas. De ahi que al tener el factor de escala $\omega$ se procura que si en el proceso de entrenamiento $Wx+b$ resulta ser muy grande, la función periódica produce una respuesta equivalente a $[ (Wx+b) \; \textrm{mod} \; 2 \pi)] - \pi$ . Es decir a la producida en la rama principal. Esto es, la capa SIREN es ciega a factores que incremeten la respuesta de la parte lineal en la forma $Wx + b + 2 k \pi$ para $k$ entera.

(Sitzmann et al., 2020) V. Sitzmann et al. Implicit Neural Representations with Periodic Activation Functions, Proc. NIPS, 2020.

Implementación

import numpy as np
from scipy.sparse import rand as sprand
import matplotlib.pyplot as plt
import PIL.Image as Image

import torch
from torch import nn
import torch.nn.functional as F
from torch.autograd import Variable
from torchvision.transforms import ToTensor, ToPILImage

print("Disponibilidad de Cuda        :",torch.cuda.is_available())

if torch.cuda.is_available():
    device = 'cuda' 
    print("Numero de dispositivos Cuda   :", torch.cuda.device_count())
    print("Dispositivo Cuda actual       :", torch.cuda.current_device())
    print("Nombre del dispositivo actual :", torch.cuda.get_device_name(torch.cuda.current_device()))
    
else:
    device = 'cpu'
    
device = 'cpu'

Disponibilidad de Cuda        : True
Numero de dispositivos Cuda   : 1
Dispositivo Cuda actual       : 0
Nombre del dispositivo actual : NVIDIA GeForce RTX 3090

img = Image.open('cameraman.pgm')
img

png

f = ToTensor()(img)[0,:,:]   # en el rango [0,1]
nrows, ncols = f.shape

nrows, ncols

(256, 256)

Creamos la base de datos, pares (posición de pixel, valor de pixel) = (X,Y)

ii, jj = np.meshgrid(np.arange(nrows), np.arange(ncols))
ii = ii.flatten().astype('float32')
ii = (ii/nrows)-0.5
jj = jj.flatten().astype('float32')
jj = (jj/ncols)-0.5
X = np.stack([ii,jj]).T
X = ToTensor()(X)[0]
X.min(),X.max(), X.shape

(tensor(-0.5000), tensor(0.4961), torch.Size([65536, 2]))

Y = f.flatten()
Y = (Y-0.5)       # en el rango [-0.5,0.5]
Y.min(),Y.max()

(tensor(-0.4137), tensor(0.5000))

from torch.utils.data import TensorDataset, DataLoader

batch_size = nrows*(ncols//10)
dataloader = torch.utils.data.DataLoader(dataset    = [*zip(X,Y)],
                                         batch_size = batch_size,
                                         shuffle    = True)

Capa SIREN

Versión comentada de la capa SIREN

class SineLayer(nn.Module):

    def __init__(self, in_features, out_features, bias=True,
                 is_first=False, is_last=False, omega_0=30):
        '''
        Implementa 
                      \sin ( omega ( W x + b) )
        
        in_features   : (int) dimensión de entrada
        out_features  : (int) número de neuronas (dimensión de salida)
        bias          : -
        is_fisrt      : (boolean) se escala distinto la inicialización de la primera capa oculta y las restantes
        is_last       : (boolean) sn funcion de activacio en la capa de salida
        '''
        
        super().__init__()
        
        self.omega_0     = omega_0
        self.is_first    = is_first
        self.is_last     = is_last
        self.in_features = in_features
        self.linear      = nn.Linear(in_features, out_features, bias=bias)
        
        self.init_weights()
        
    def forward(self, input):
        '''
             y = Phi(omega0 W (x+b) )
        '''
        return torch.sin(self.omega_0 * self.linear(input))
    
    def forward_with_intermediate(self, input): 
        '''
             z =  omega0  (W x + b)
             y = \sin(z)
             (y,z)
        '''
        # For visualization of activation distributions
        z = self.omega_0 * self.linear(input)
        return torch.sin(z), z if not self.last else z,z
        
    def init_weights(self):
        '''
        Inicialización escalada para considerar a la activación periodica 
        
        Pretende mantener la respuesta de cada neurona dentro de una misma rama y 
        evitar saltos entre ramas al entrenar los pesos
        '''
        with torch.no_grad():
            if self.is_first:
                self.linear.weight.uniform_(-np.sqrt(1 / self.in_features), 
                                             np.sqrt(1 / self.in_features ))     
            else:
                self.linear.weight.uniform_(-np.sqrt(6 /self.in_features)  / self.omega_0, 
                                             np.sqrt(6 / self.in_features) / self.omega_0)

MLP con capas SIREN

Ahora el modelo de la red es un perceptrón multicapa con capas SIREN (MLP-SIREN).

class SIRENnet(nn.Module):
    def __init__(self, input_dim, hidden_dims, output_dim=1):
        #super(MLPnet, self).__init__()
        super().__init__()
        '''
        El método init define las capas de las cuales constará el modelo, 
        aunque no la forma en que se interconectan
        '''
        # Modelo inicialmente vacio
        self.net = []
        
        # Se agragan capas Seno ocultas
        is_first=True
        for i in range(len(hidden_dims)):
            is_last = False if i < len(hidden_dims)-1 else True

            self.net.append(SineLayer(in_features  = input_dim, 
                                      out_features = hidden_dims[i], 
                                      is_first     = is_first,
                                      is_last      = is_last))
            input_dim = hidden_dims[i]
            is_first=False
        
        self.net = nn.Sequential(*self.net)
                
    def forward(self, x):
        out=self.net(x)
        return out
    
    def name(self):
        return "MLP"

model = SIRENnet(input_dim=(2), hidden_dims=[128,128, 128, 128, 1], output_dim=1)

implicit siren model

model_parameters = filter(lambda p: p.requires_grad, model.parameters())
params = sum([np.prod(p.size()) for p in model_parameters])
params, 256*256

(50049, 65536)

Entrenamiento del modelo

model = model.to(device)
rec_loss = torch.nn.MSELoss() # L1Loss() #
optimizer = torch.optim.Adam(model.parameters())

num_epochs = 100
loss_list = []

for epoch in range(num_epochs):
    
    loss_epoch =0
    # - - - - - - - - - - - - - - - 
    # Entrena la Red en lotes cada época
    # - - - - - - - - - - - - - - - 
    for i, (x, y) in enumerate(dataloader):        
        x = x.to(device)
        y = y.to(device)
        x = Variable(x) 
        y = Variable(y)
        
        optimizer.zero_grad()                  # Borra gradiente
        y_pred = model(x)                      # Propagación
        loss   = rec_loss(y_pred[:,0],y)       # Calcula error
        loss.backward()                        # Retropropaga error
        optimizer.step()                       # Actualiza parámetros
        loss_epoch += loss.data
        
    # - - - - - - - - - - - - - - - 
    # Despliega evaluación
    # - - - - - - - - - - - - - - - 
    loss_list.append(loss_epoch/i)
    print('Epoch: {:03}/{}  Loss: {:.6f}'.format(epoch, num_epochs,loss_list[-1]))

Epoch: 000/100  Loss: 0.562069
Epoch: 001/100  Loss: 0.504904
Epoch: 002/100  Loss: 0.505939   
...
Epoch: 098/100  Loss: 0.001744
Epoch: 099/100  Loss: 0.001795

torch.save(model, 'model_implicit.pt')

Despliege de la reconstrucción

Y_pred=model(X.to(device))
y_pred = Y_pred.detach().cpu().numpy().reshape(nrows,ncols)

plt.figure(figsize=(10,5))
plt.subplot(121)
plt.imshow(y_pred, 'gray')
plt.axis('off')
plt.subplot(122)
plt.imshow(f, 'gray')
plt.axis('off')

(-0.5, 255.5, 255.5, -0.5)

png

history_loss = [v.item() for v in loss_list]        

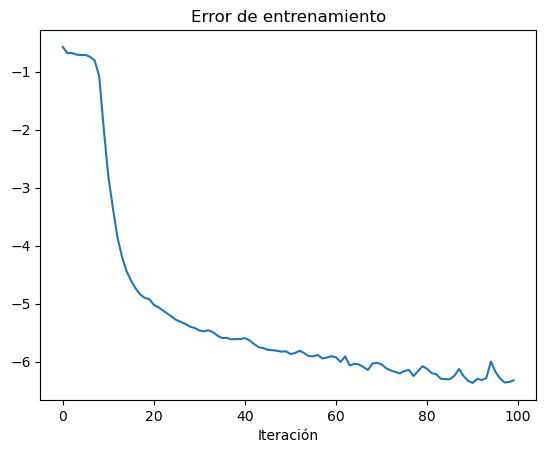
fig, ax = plt.subplots()
ax.plot(np.log(history_loss))
ax.set_title('Error de entrenamiento')
ax.set_xlabel('Iteración')
plt.show()

png