Redes Generadoras Antagónicas

Generative Adversarial Networks (GANs)

Código de ejemplo basado en el del Capítulo 2 de Langr and Bok (2019).

Mariano Rivera

Enero 2019

import os
os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID";
os.environ["CUDA_VISIBLE_DEVICES"]="1";

El modelo de redes profundas Redes Antagónicas Generadoras (Generative Adversarial Networks, GANs) fue propuesto por Goodfellow et al., 2014b.

Las GANs son un modelo generador (de los muchos que existen) que se basa en redes neuronales profundas.

Un modelo Generador es aquel que a partir de datos $x$ aprende la distribución subyacente $P(x)$ la cual puede ser muestreada para generar nuevos datos $\tilde x$ con la misma distríbución

En la sección Autocodificadores Variacionales (VAEs) se presenta un método que codifica implícitamente (en una DNN, codificador) la distribución subyacente $P(x) = P(x|z) P(z)$ (donde $z$ son variables latentes). Mediante la optimización de la cota variacional (ELBO)

${L}_{VAE} \le \log P(x)$

como estrategia de Máxima Verosimilitud (Maxmimum Likelihood, ML), toda vez que estimamos parámetros que incrementen $\mathcal{L}_{VAE}$ , nos acercaremos a la cota superior que es el estimador de ML. Se ha observado que, si bien la estrategia basada en VAEs estiman una muy buena verosimilitud, la muestras generadas con estos métodos son de baja calidad (Goodfellow et al., 2014b). Cabe notar que la evaluación de la calidad de las muestras se realiza en mediante una inspeción subjetiva: visual en imágenes o auditiva en audio.

El siguiente código python produce datos con distribución Gaussiana, estima los parámetros de dicha distribución y muestrea la distribución Gaussianan estimada. La gráfica presenta los datos y las muestras generadas.

import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt

# Genera muestra aleatoria
#np.random.seed(0)
m = 100  # numero de datos 
C = np.array([[0.1, .1], [.1, .4]])
Xdat = np.random.randn(m, 2)
Xdat = Xdat@C + [1., 2.]

#Ajuste del modelo Gaussiano
mu    = Xdat.mean( axis=0)
Sigma = np.cov(Xdat.T)

# Muestra la distibución subyacente
Xsmp = np.random.multivariate_normal(mu, Sigma, size=m)

#plotea los datos y las muestras de la dirtibución subyacente
plt.figure(figsize=(5,5))
plt.scatter(Xdat[:,0], Xdat[:,1])
plt.scatter(Xsmp[:,0], Xsmp[:,1], marker='+')
plt.title('Datos `o` y Muestras `+`')
plt.show()

png

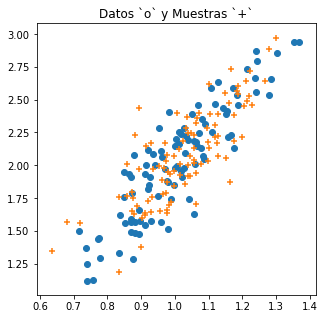
A diferencia del ejemplo ilustrado con datos con distribución Gaussiana bi-valuada, los datos de nuestro interés son muy complejos y por ende sus distribuciones,

El propósito es dado un conjunto de datos

(1)
$X = \begin{bmatrix} x_1^\top \\ x_2^\top \\ \vdots \\ x_m^\top \\ \end{bmatrix}$

estimar la densidad subyacente

(2)
$P(x)$

que permita ser muestreada. Los datos $x$ son generamente complejos y en altas dimensiones; como imágenes, texto, señales, etc. Lo relevante del problema es que es del tipo no supervisado, es decir los datos no estan etiquetados.

Para representar la densidad $P(x)$ , es importante contar con modelos de gran capacidad, por lo que no tendremos una expresión que la defina, sino que será codificada en forma de una red neuronal profunda. Las GANs nos permiten muestrear distribuciones subyacentes de datos tan complejos como las imágenes de los dígitos MNIST o de bases de datos de rostros, etc.

El contar con modelos generativos de datos complejos en altas dimensiones es de primordial importancia en muchos de los problemas actuales de las ciencias e ingeniería. El poder generar datos sintéticos realistas nos permitirá reducir el número de muestras requeridas para entrenar redes profundas. Además que es posible construir sistemas generadores de datos que correspondan a situaciones hipotéticas y poder evaluar modelos de toma de descición ante tales eventualidades.

Los modelos generadores de gran capacidad se basan generalmente en redes neuronales profundas, en la siguiente figura ilustramos una clasificación de acuerdo a Goodfellow et al., (2014b) en la que se muestra la relacion entre los Autoencoders Variacionales (VAEs) y las Redes Antagónicas Generadoras (GANs).

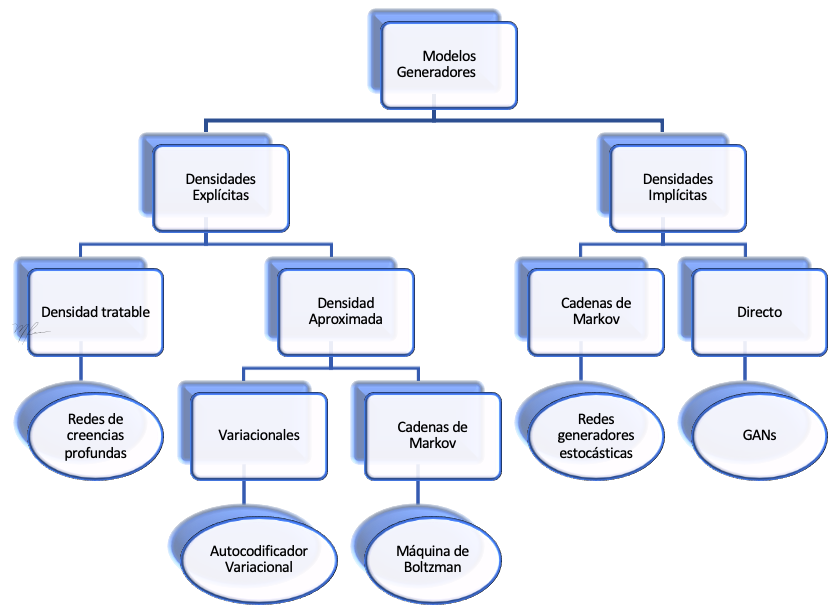
taxonomia

Las GANs estan diseñadas para aprender la densidad subyacente de datos $X$ y representarlas en forma implícita. Las GANS se pueden ver como dos DNN: un generador y un discriminador.

El propósito del Generador $G$ es generar datos sintéticos $\tilde x$ que sean indistinguibles de los datos reales para el Discriminador $D$ . Por lo que el discriminador es una red que clasifica datos que se le presentan entre reales o falsos (fakes).

Una analogía frecuentemente usada para explicar el comportamiento de las GANs es el de un aprendiz de falsificador de arte y un joven curador que pretende detectar el arte falso. Para ello, de lo que disponemos es de ejemplos de arte válido (ejemplos positivos). Luego se le pide al joven falsificador que haga unas imitaciones, para lo cual tienen poco conociento (sus dibujos son de calidad de jardín de niños) y al jóven curador se le pide que indique que obras son reales y cuales no (sin siquiera saber que artista las pintó). Cada vez que el curador clasifica una obra, puede resultar que acierte en detectar si es o no falsa, y dicha evaluacion de su desempeño se le notifica. Igualmente, al joven falsificador se le informará si una obra pintada por él fue detectada como falsificación o logró confundir al curado. Dado que el joven falsificador empieza desde un nivel muy básico, para el curador será en un inicio muy fácil el distingur despues de unas cuantas piezas analizadas sobre cual es el estilo pictórico de las obras reales y cuales el de los garabatos del falsificador. Esperemos pues que el Curador tenga rápido un muy buen desempeño y el falsificador tenga uno bajo. Sin enmabrgo, el falsificador al ser retroalimentado sobre sus malas imitaciones recibe información sobre lo que no debe hacer e irá explorando nuevos trazos, eventualmente podra engañar al curador con unas pocas obras, lo que reforzará su conocimiento sobre que es lo adecuado. Esta competencia entre el falsificador y e curador por mejorra su desempeño es un “juego” en el que gana el curador si siempre detecta las falsificaciones o gana el falsificador si la respuesta del curador se convierte en prácticamente una decisión de aleatoria. Si lo que queremos es tener un excelente generador de obras de arte, debemos promover una estartegia de aprendizaje que le permita falsificador aprender rápidamente. Una estrategia es usar una etapa de calentamiento (burning) que ponga falsificador con un otro aprendiz de curador a competir, y luego que ya tienen cierto desempeño (sus trazos sean razonables), ahora si se le pone frente al competidor real. Esto se implementa ejecutando el entrenamiento y luego un cierto número de iteraciones se borra la memoria (se borran los pesos) del discriminador, dejando al generador con las habilidades adquiridas (se dejandole intactos sus pesos).

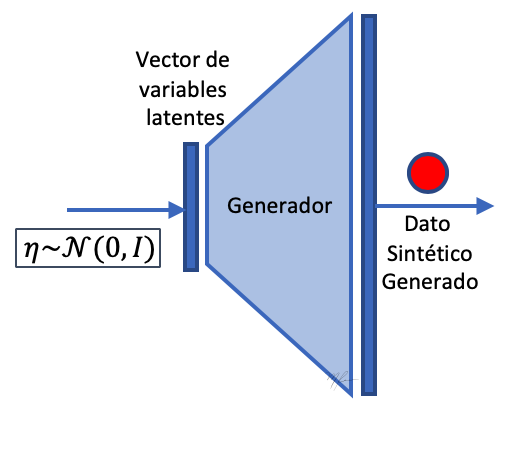
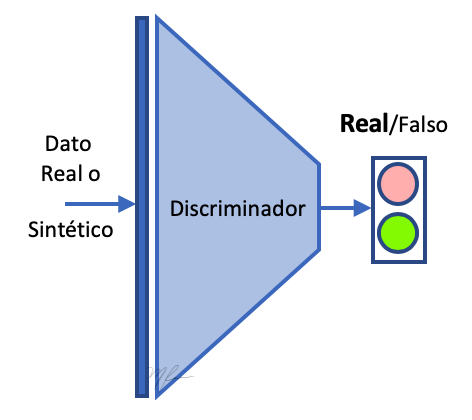
En la siguiente figura mostramos el esquema general de una GAN.

gan

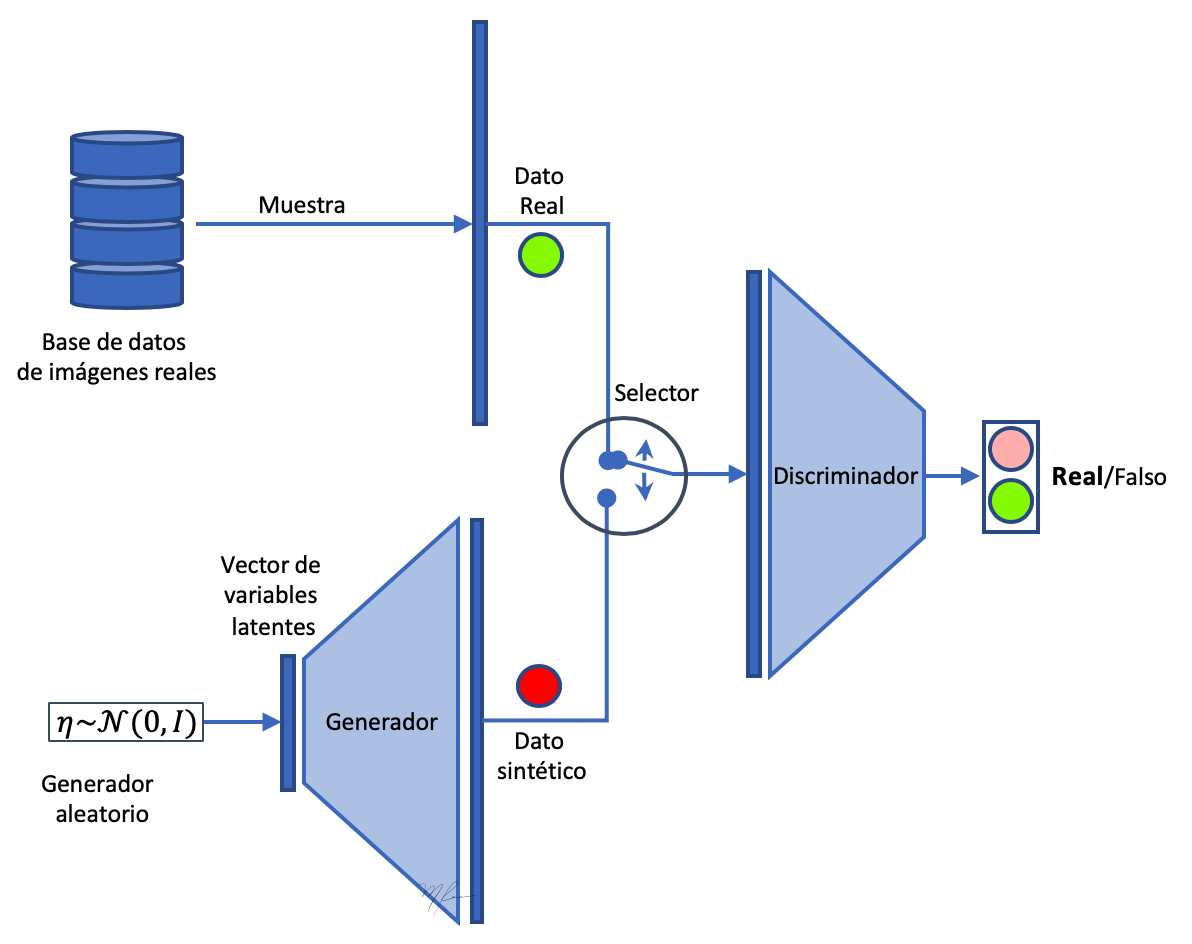
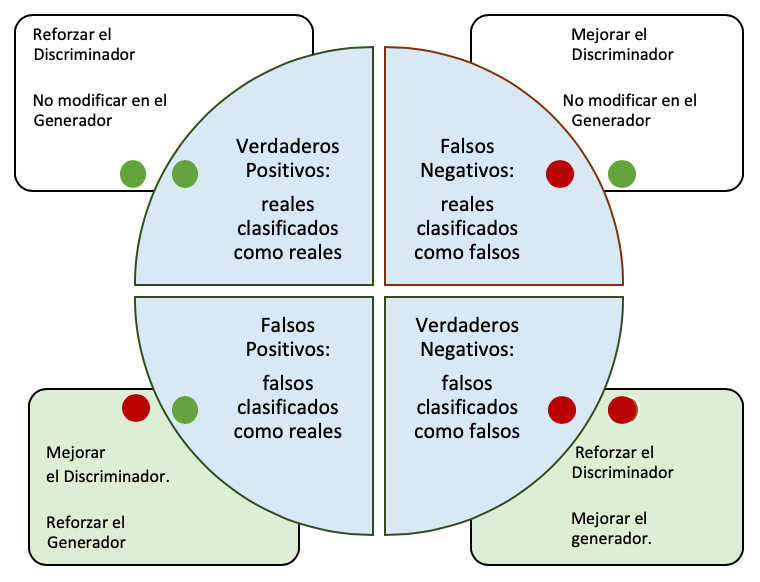
En la figura se ilustra como el generador produce datos a partir de variables latentes, estos datos son mezclados con datos reales y la tarea del discriminador es distinguir que datos son reales y que datos son sintéticos. Cada vez que el discriminador evalua un dato, su respuesta es evaluada como correcta o incorrecta. El valor del error es retroalimentado al Discriminador y al Generador. Si el discriminador acertó al clasificar la imágen, los pesos del discriminador no requiren de ser ajustados (en todo caso reforzados). El generador que deberá ajustarse para producir mejores datos; si el dato era real y fue clasificado correctamente, entonces no se debe modificar el generador. De igual manera, si el discriminador falla al clasificar un dato sintético, se deberá ajustar el discriminador y no habrá necesidad de modificar el generador. En la siguiente figura se resume lo dicho.

estrategias

poner al Discriminador como una red clasificadora.
poner al Generador como una red generadora.
decir como se entrena el discriminador a partir de imágenes dadas (real y fake).
construir el modelo del GAN con el discriminador congelando sus pesos (no entrenable).
entrenar alternadamente.

Función Objetivo de la GAN

Sean $y \in \{0,1\}$ la etiqueta del dato $x$ correspondientes a “falso” o “real” y $\hat y \in [0,1]$ su estimación obtenida del discriminador para el dato en cuestión. Luego, la función a optimizar mediante el entrenamiento de la GAN esta dada por la cross entropía binaria:

(1)
$J(\hat y; y) = \sum_{i} y_i \log \hat y_i + (1-y_i)\log (1-\hat y_i)$

pero la clasificación $\hat y$ puede obtenerse a partir de un dato real $x$ o de uno falso $x(z)$ . Separando los casos de $y=1$ para datos reales y $y=0$ para datos falsos, el probema de optimización nos queda como

(2)
$\underset{\theta_d}{\max} \underset{\theta_g}{\min} \sum_{x \in data} \log \hat y_i(x, \theta_d) + \sum_{z \sim p_g(z)} \log [1-\hat y_i(z, \theta_d, \theta_g)]$

donde

$\hat y_i(x, \theta_d)$ es la respuesta del discriminador al dato real $x$ ;
$\hat y(z, \theta_d, \theta_g)$ es la respuesta del discriminador al falso $x(z)$ , generado a partir de la variable latente $z$ ;
$\theta_d$ son los parámetos del discriminador y
$\theta_g$ son los parámetos del generador.

Ahora, sean $D$ y $G$ las redes representacionales del discriminador y generador, respectivamente; entonces, de acuerdo a Goodfellow (2016b), la función de pédida (2) se reescribe como

(3)
$\underset{\theta_d}{\min} \underset{\theta_g}{\max} \sum_{x \in data} \log D(x;\theta_d) + \sum_{z \sim p_g(z)} \log [1-D(G(z; \theta_g);\theta_d)]$

Note que la optimización del Generador intentará encontrar parámetros que confundan al Discriminador: que etiqueten datos falsos como reales, con $\hat y(z) \approx 1$ . Luego $\log [1-D(G(z; \theta_g);\theta_d)] << 0$ , lo que es conveniente para minimizar la función de pérdida respecto al generador.

Estrategia de entrenamiento de la GAN

A continuación damos el esquema general a seguir para entrenar una GAN.

for t in n-Iterations:

Generar un lote de variables latentes $z=\{z_1, z_2, \ldots, z_m\}$ con $p(z)$ % Generalmente $p(z) \sim \mathcal{N}(0,\mathbb{1})$
Leer un lote de imágenes reales $x=\{x_1, x_2, \ldots, x_m\}$ .
Actualizar el discriminador mediante la solución aproximada de
$\underset{\theta_d}{\min} \sum_{x_i} \log D(x;\theta_d) + \sum_{z_i} \log [1-D(G(z_i; \theta_g);\theta_d)]$
Actualizar el generador mediante la solución aproximada de
$\underset{\theta_g}{\max} \sum_{z_i} \log [1-D(G(z_i; \theta_g);\theta_d)]$

end for

Referencias

(Langr & Bok, 2019) Jakub Langr and Vladimir Bok, GANs in Action, MEAP Ed. Manning Publications Co, 2019.

(Goodfellow et al., 2014b) Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014b). Generative adversarial net- works. In NIPS’2014. Pdf versión arXiv

(Goodfellow et al., 2016a) Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT Press. http://www.deeplearningbook.org.

(Goodfellow,2016b) Ian Goodfellow, NIPS 2016 Tutorial: Generative Adversarial Networks, arXiv 1701.00160, 2016.

%matplotlib inline

import sys
import numpy as np
import matplotlib.pyplot as plt

from keras.datasets import mnist
from keras.layers import Input, Dense, Reshape, Flatten
from keras.layers import Activation
from keras.layers.advanced_activations import LeakyReLU
from keras.models import Sequential, Model
from keras.optimizers import Adam

Using TensorFlow backend.

img_rows, img_cols, channels  = 28, 28, 1
img_shape = (img_rows, img_cols, channels)
z_dim = 100 # dimensión del espacio latente

data_sz = img_rows*img_cols*channels

Generador

En generador es una red neuronal secuencial profunda que recibe de entrada un vector de variables latentes y produce datos en altas dimensiones.

generador

def generator(img_shape, z_dim):
    '''
    Construye el modelo de la DNN Generadora
    
    parámetros:
    img_shape     dimensiones de los datos generados
    z_dim         dimensiones del espacio latente
    
    resultados:
                  regresa el modelo de DNN generadora 
    '''
    # construcción de `model` secuencial usando Keras clásico (no la API)
    model = Sequential()    
    # Capa oculta 1
    model.add(Dense(units=128, input_dim=z_dim))
    # Activacion de capa oculta 1:  relu-leaky
    model.add(LeakyReLU(alpha=0.01))
    # Capa oculta 2
    model.add(Dense(units=data_sz, activation='tanh'))
    # Reshape  a la salida para formato de imagen
    model.add(Reshape(img_shape))
    
    # construcción del modelo que regresa la función `generator` usando la API y 
    # el `model` definido arriba
    z = Input(shape=(z_dim,))
    img = model(z)
    # regresa el modelo generador construido
    return Model(z, img)

Construye el Generador

generator = generator(img_shape, z_dim)

Discriminador

En discriminador es una red neuronal secuencial profunda que recibe de entrada un vector datos y produce una clasificación indicando si los datos son reales o falsos (fake).

discriminador

def discriminator(img_shape):
    '''
    Construye el modelo de la DNN Discriminadora
    
    parámetros:
    img_shape     dimensiones de los datos a analizar
    
    resultados:
                  regresa el modelo de DNN discriminadora 
    '''
    
    # construcción de `model` secuencial usando Keras clásico (no la API)
    model = Sequential()
    model.add(Flatten(input_shape=img_shape))
    # Capa Oculta 1
    model.add(Dense(units=128))
    # Activación de capa oculta 1: relu-leaky
    model.add(LeakyReLU(alpha=0.01))
    # capa de salida (clasificación)
    model.add(Dense(1, activation='sigmoid'))

    # construcción del modelo que regresa la función `discriminator` usando la API y 
    # el `model` definido arriba
    img = Input(shape=img_shape)
    prediction = model(img)
    
    # regresa el modelo discriminador construido
    return Model(img, prediction)

from keras import backend as K

# Resetea los pesos del modelo 
def reset_weights(model):
    session = K.get_session()
    for layer in model.layers: 
        if hasattr(layer, 'kernel_initializer'):
            layer.kernel.initializer.run(session=session)

Construye y compila el Discriminador

El Discriminador (modelo discriminator) no es entrenable durante el entrenamiento del Generador

# construye el discriminador 
discriminator = discriminator(img_shape)

# compila en discriminador 
discriminator.compile(loss='binary_crossentropy', 
                      optimizer=Adam(), 
                      metrics=['accuracy'])

# Congela los parámetros del discriminador durante el entrenamiento del generador
discriminator.trainable = False

Construcción del modelo GAN Combinado

El modelo GAN incluye la generación y la discriminación.

# genera imagen 
z = Input(shape=(100,))
img = generator(z)
# predice etiqueta de la imagen 
prediction = discriminator(img)

gan = Model(z, prediction)
gan.compile(loss      = 'binary_crossentropy', 
            optimizer = Adam())

Entrenamiento

El algoritmo para entrenar la GAN es descrito como sigue

Iterar por n iteraciones:

Entrena el Discriminador:

1.1 Carga lote de imagenes reales $X_r$

1.2 Genera lote de imágenes falsas $X_f$

1.3 Ajusta (entrena) el discriminador con la imagenes reales $X_r$

1.4 Ajusta (entrena) el discriminador con la imagenes falsas $X_f$
Entrena el Generador:

2.1 Usando el lote de imágenes falsas, $X_f$ , ajustar los pesos de la GAN

losses = []
accuracies = []

def train(iterations, batch_size, sample_interval):
    
    # carga datos reales     
    (X_train, _), (_, _) = mnist.load_data()

    # Rescale -1 to 1
    X_train = X_train / 127.5 - 1.
    X_train = np.expand_dims(X_train, axis=3)

    # Etiquetas de ejemplos reales (1) y falsos (0)
    real = np.ones((batch_size, 1))
    fake = np.zeros((batch_size, 1))

    for iteration in range(iterations):
        
        # -------------------------
        #  Entrena el Discriminador
        # -------------------------

        # batch aleatorio de imagenes reales
        idx = np.random.randint(0, X_train.shape[0], batch_size)
        imgs = X_train[idx]

        # batch generado aleatoriamente de imagenes falsas
        z = np.random.normal(0, 1, (batch_size, 100)) 
        gen_imgs = generator.predict(z)

        # Pérdida del discriminador
        d_loss_real = discriminator.train_on_batch(imgs, real)
        d_loss_fake = discriminator.train_on_batch(gen_imgs, fake)
        d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)

        # ---------------------
        #  Entrena el Generador
        # ---------------------

        # batch aleatorio de imagenes falsas
        # importante que sean otras diferentes al lote usado en discriminador, pues 
        # ese ya las vio en el paso previo de entrenamiento
        z = np.random.normal(0, 1, (batch_size, 100))
        gen_imgs = generator.predict(z)

        # Entrena Generador (en realidad todo el GAN)
        g_loss = gan.train_on_batch(z, real)

        # ---------------------
        #  Registra avances
        # ---------------------
        
        if iteration % sample_interval == 0:
            
            # Reporte del avance del entrenamiento
            print ("%d [D loss: %f, acc.: %.2f%%] [G loss: %f]" % 
                         (iteration, d_loss[0], 100*d_loss[1], g_loss))
            
            # Salva pérdidas y precisiones
            losses.append((d_loss[0], g_loss))
            accuracies.append(100*d_loss[1])

            # Salida de imágenes reneradas
            sample_images(iteration)

def sample_images(iteration, image_rows=4, image_columns=4):
    # muestreo del generador usando ruido aleatorio para la variable latente
    z = np.random.normal(0, 1,(image_rows * image_columns, z_dim))

    # Generación de imágenes falsas
    gen_imgs = generator.predict(z)
    gen_imgs = 0.5 * gen_imgs + 0.5  # reescala [0,1]
    nrows, ncols = gen_imgs[0,:,:,0].shape 
    
    # Grafica imágenes generadas
    fig = plt.subplots(figsize= (6,6))
    
    canvas = np.ones((image_rows*nrows,image_columns*ncols))
    cont = 0
    for i in range(image_rows):
        for j in range(image_columns):
            ii = i*nrows
            jj = j*ncols
            canvas[ii:ii+nrows,jj:jj+ncols] = gen_imgs[cont, :,:,0]
            cont += 1
            
    plt.imshow(canvas, cmap='gray')
    plt.axis('off')

Entrena el modelo

# Suprime WARNINGS de Keras debido a parámetros no entrenables por diseño:
# el generador es congelado mientras se entrena el discriminador
import warnings; warnings.simplefilter('ignore')

# Entrena  el GAN

iterations      = 20000
batch_size      = 128
sample_interval = 1000

train(iterations = iterations, 
      batch_size = batch_size, 
      sample_interval=sample_interval)

0 [D loss: 0.652001, acc.: 60.16%] [G loss: 0.870783]
1000 [D loss: 0.086948, acc.: 100.00%] [G loss: 3.445611]
2000 [D loss: 0.059547, acc.: 98.44%] [G loss: 4.772520]
3000 [D loss: 0.146943, acc.: 94.14%] [G loss: 4.701931]
4000 [D loss: 0.061868, acc.: 99.22%] [G loss: 4.861426]
5000 [D loss: 0.162849, acc.: 92.97%] [G loss: 4.886634]
6000 [D loss: 0.368400, acc.: 82.03%] [G loss: 2.770931]
7000 [D loss: 0.289607, acc.: 89.45%] [G loss: 4.370484]
8000 [D loss: 0.338264, acc.: 86.33%] [G loss: 4.464498]
9000 [D loss: 0.548789, acc.: 79.30%] [G loss: 2.895535]
10000 [D loss: 0.435969, acc.: 82.42%] [G loss: 2.717033]
11000 [D loss: 0.466841, acc.: 79.69%] [G loss: 3.069324]
12000 [D loss: 0.242352, acc.: 89.06%] [G loss: 2.946186]
13000 [D loss: 0.307539, acc.: 85.55%] [G loss: 3.456585]
14000 [D loss: 0.303654, acc.: 85.94%] [G loss: 3.391770]
15000 [D loss: 0.559385, acc.: 76.17%] [G loss: 2.280031]
16000 [D loss: 0.286092, acc.: 85.16%] [G loss: 2.756658]
17000 [D loss: 0.579837, acc.: 74.22%] [G loss: 2.091316]
18000 [D loss: 0.314228, acc.: 87.11%] [G loss: 2.662951]
19000 [D loss: 0.297424, acc.: 88.67%] [G loss: 2.628417]

png
png
png

…

png
png

gan.save_weights('model_gan_.h5')

Después del Burning

reset_weights(discriminator)

# Entrena  el GAN
iterations      = 20000
batch_size      = 128
sample_interval = 1000

train(iterations = iterations, 
      batch_size = batch_size, 
      sample_interval=sample_interval)

0 [D loss: 0.376366, acc.: 82.42%] [G loss: 2.265726]
1000 [D loss: 0.388683, acc.: 82.42%] [G loss: 2.210185]

…

2000 [D loss: 0.306628, acc.: 86.33%] [G loss:     19000 [D loss: 0.425922, acc.: 80.86%] [G loss: 2.111063]

png
png
png

…

png
png

gan.save_weights('model_gan_.h5')

En definitiva, aunque mejoraron respecto al burning, las imágenes generadas no son de buena calidad. Esto se debe a que nuestro generador debe aprender las relaciones espaciales entre los pixeles a generar, y ello no es fácil para una red Densa. Por lo que implementaremos la versión convolucional de esta GAN en la siguiente sección.