Visualización de Filtros

Basado en el blog de Chollet Vizualization What ConvNet Learn

Mariano Rivera

Marzo 2023

Aprendizaje Automático, Mariano Rivera, CIMAT © 2023

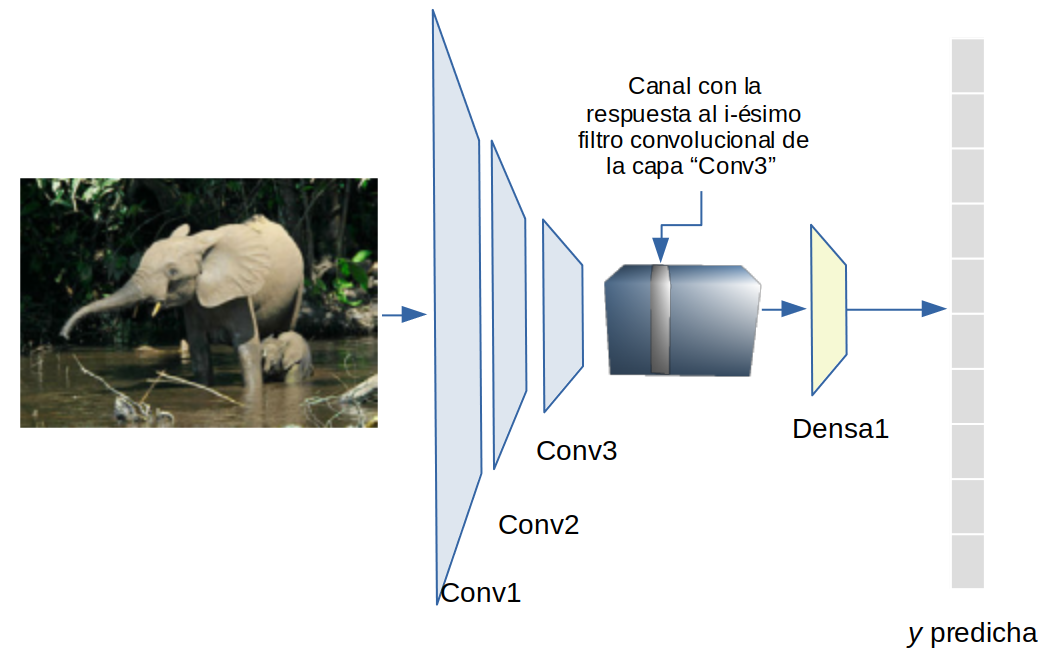
Visualización los patrones a los que un filtro convolucional particular responde

Sabemos en las primera capa oculta, los pesos de una red estan correlacionados con los rasgos a detectar. También que los pesos de una neurona convolucional pueden interpretarse como los pesos de un filtro de convolución. Así una neurona se activará si existe una alta correlación entre la máscara de pesos aprendida y la región en la imagen sobre el cual se sobrepone. La siguiente capas, se pueden interpretar a partir de la combinación de los fitros básicos.

La forma de visualizar que carácterística detecta un filtro particular es calculando la imagen de entrada que maximiza la respuesta en una neurona oculta (filtro). Esto es,

• Primero se fijan los pesos de la CNN.

• Luego, mediante “ascenso” de gradiente se maximiza una función de costo que representa la activación de una neurona oculta con respecto a la imagen de entrada.

La imagen de entrada que maximiza la respuesta de una neurona contendrá el tipo de rasgos que dicha neurona detecta.

Es posible ver que a medida que al nerona es mas profunda (cercana a la capa de salida) la image de entrada irá conteniendo rasgos cada vez mas complejos.

Entonces, lo que vemos es que la estructura espacial de la imagen es descompuesta en rasgos a través de las capas de procesamiento. Así, la respuesta espacial de un filtro en una capa oculta esta espacialmente correlacionado; pues la respuesta en la primera capa estaba correlacionada, y la segunda capa tandrá una entrada espacialmente correlacionada, por lo que su salida será también correlacionada; y así para las siguientes capas.

Matemáticamente, el procedimiento consiste en calcular la imagen que maximiza la respuesta $y_{i k}$ del filtro $f_{i k}$ ($i$-ésimo filtro de la capa k). Para ello definimos una pérdida (loss):

(1)
$$L(y_{i k}) = \sum_{m,n} y_{i k m n}.$$

Que es una medida de la respuesta obtenida por el filtro $f_{ik}$. Luego derivamos el costo respecto a la imagen de entrada $x$:

(2)
$$g_{i k} = \nabla_x L(y_{i k}).$$

Dado que nuestro propósito es encontrar la imagen x que “maximice” la respuesta $y_{i k}$, realizamos ascenso de gradiente (note el signo +):

(3)
$$x^{t+1} = x^{t} + \alpha \frac{g_{i k}}{\| g_{i k} \|}$$

Donde $\alpha$ es el tamaño de paso y hemos normalizador el gradiente y $x$ se inicializa con ruido.

Implementación

import numpy as np
from PIL import Image
import requests

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.applications import ResNet50V2,VGG16

print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))

Num GPUs Available:  1

Asumimos que la red que nos interesa analizar ya ha sido previemente entrenada. De ejemplo se usa la red ResNet50V2 prentrenada con ImageNet.

input_shape = (224,224,3)
model = ResNet50V2(weights     = "imagenet", 
                   include_top = False,  
                   input_shape = input_shape)

Visualizaremos filtros en la última capa convolucional

Construimos un modelo desde la imágen de entrada hasta la capa seleccionada; conv3_block4_outen este caso

layer_name        = "conv3_block4_out"
layer             = model.get_layer(name=layer_name)
feature_extractor = keras.Model(inputs=model.inputs, outputs=layer.output)

Construimos una función de costo que maximiza la activación enn la capa de salida para un filtro en particular

def compute_loss(model, input_image, filter_index):
    activation = model(input_image)
    # Para evitar artefactos no involucramos pixeles en los bordes (recomendación de Chollet)
    filter_activation = activation[:, 2:-2, 2:-2, filter_index]
    return tf.reduce_mean(filter_activation)
    

Ascenso de gradiente

(4)
$$x \leftarrow x + \alpha \frac{\nabla f}{\| {\nabla f}\|}$$

El decorador @tf.function indica que la función esta implementadad con operaciones de tensorflow, por lo que ser ejecutada en en paralelo y GPU.

@tf.function
def gradient_ascent_step(model, img, filter_index, learning_rate, ):
    with tf.GradientTape() as tape:
        tape.watch(img)
        loss = compute_loss(model, img, filter_index)
    
    # calcula gradiente y lo normaliza para evolucion suave de la imagen
    grads = tape.gradient(loss, img)
    grads = tf.math.l2_normalize(grads)

    # ascenso de gradiente
    img += learning_rate * grads
    return loss, img

Inicialización de la imágen de entrada con ruido uniforme cercano a cero:

$$x \sim U(-0.025, 0.0025)$$

def initialize_image(url=None):
    # imagen de ruido com media en la media del rango dinámico
    img = tf.random.uniform(input_shape)
    img = tf.expand_dims(img, axis=0)
    img = (img - 0.5) * 0.25  # Resnet  espera entrada en el rango [-1,1]
    if url:   # imagen base para algo como DeepDream
        im      = Image.open(requests.get(url, stream=True).raw)
        img_ref = im.resize((224, 224))
        img_ref = np.array(img_ref).astype('float32')
        img    += (img_ref/127.5)-1
    return img 

Pasa la imagen de entrada $x^{t}$ a un rango que pueda ser desplegada

def deprocess_image(img):
    # normaliza la imagen: media 0, y var 0.15
    img -= img.mean()
    img /= img.std() + 1e-5
    img *= 0.15
    # toma solo el centro
    img = img[25:-25, 25:-25, :]
    # Clip to [0, 1]
    img += 0.5
    img = np.clip(img*255, 0, 255)
    return img.astype(np.uint8)

Equivalente al ciclo train,

• Inicializa la imagen.
• Calcula:
  • Función de costo
  • Gradiente
  • Paso de ascenso
• Pone la imágen en el rango desplegable.

def visualize_filter(model=None, filter_index=0, iterations=300, learning_rate =10.0, url_img=None):
    
    img = initialize_image(url_img)
    for iteration in range(iterations):
        loss, img = gradient_ascent_step(model, img, filter_index, learning_rate)
        if iteration%50==0:
            print('.',end ='')
    # decodifica la salida como numpy
    img = deprocess_image(img[0].numpy())
    return loss, img

Realizamos el cálculo

loss, img = visualize_filter(model         = feature_extractor, 
                             filter_index  = 51, 
                             iterations    = 50, 
                             learning_rate = 10.0,
                            )

.

import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
plt.imshow(img[25:-25,25:-25,:])
plt.imsave('img_filter.png',img)

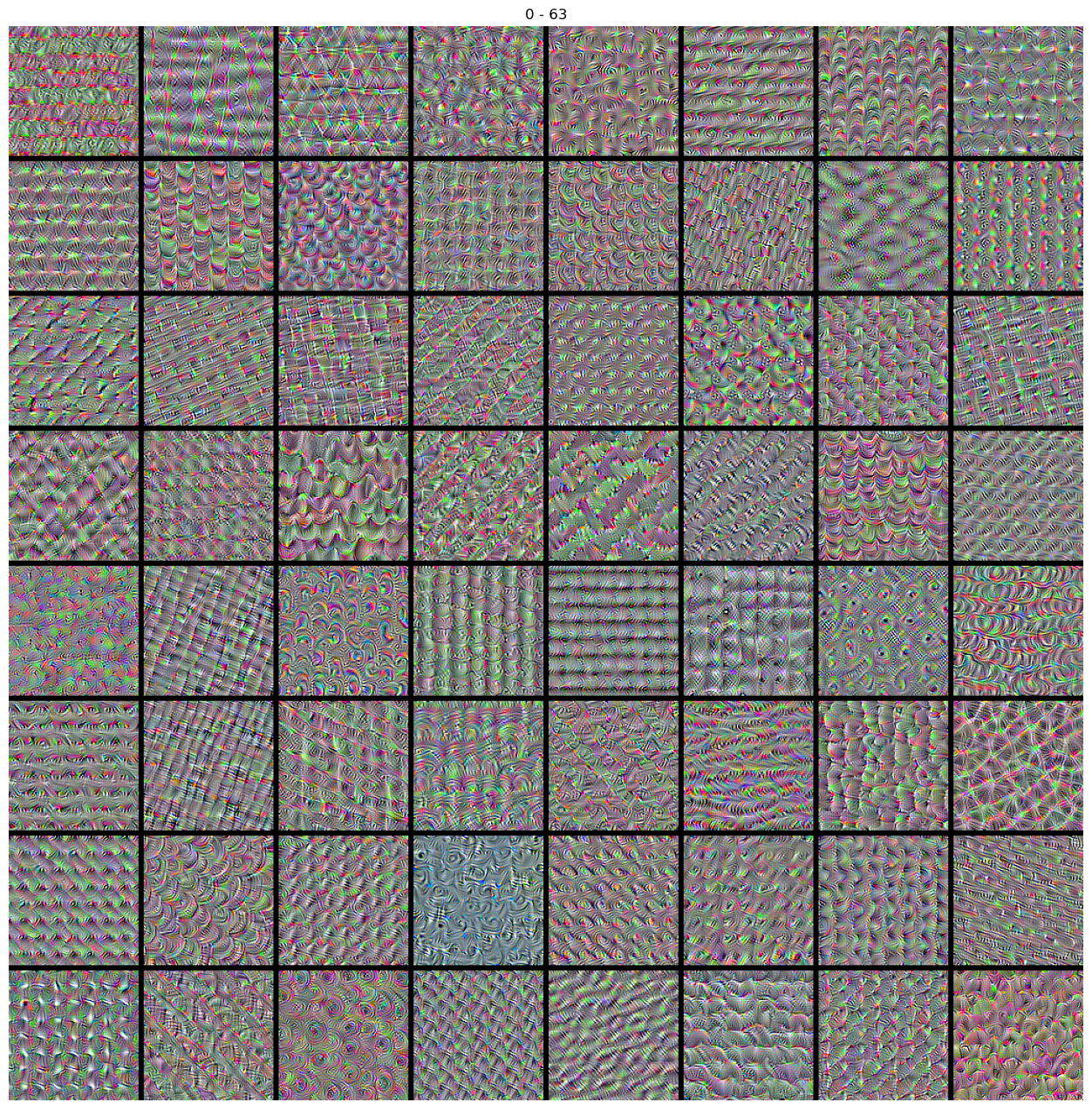
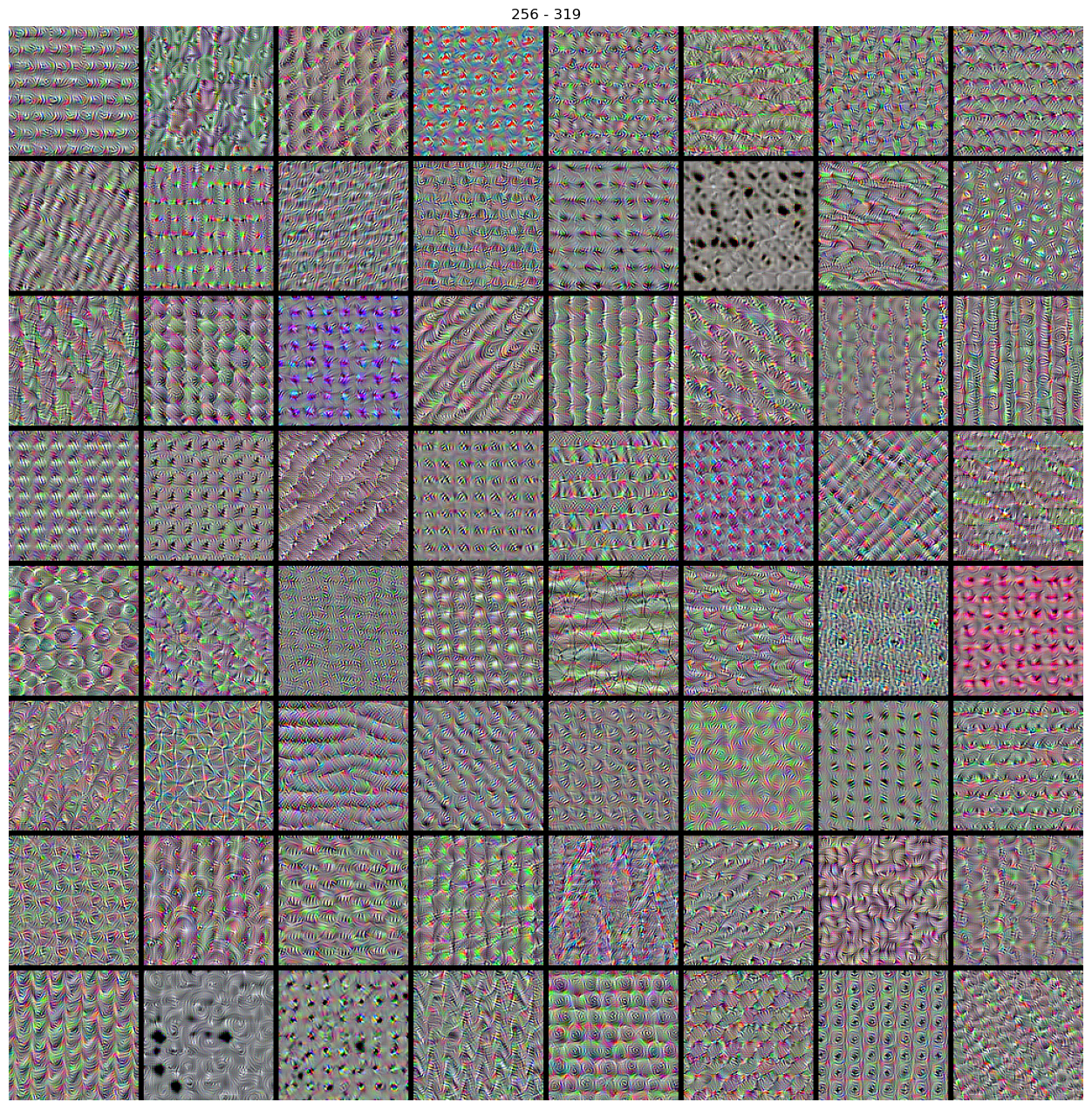
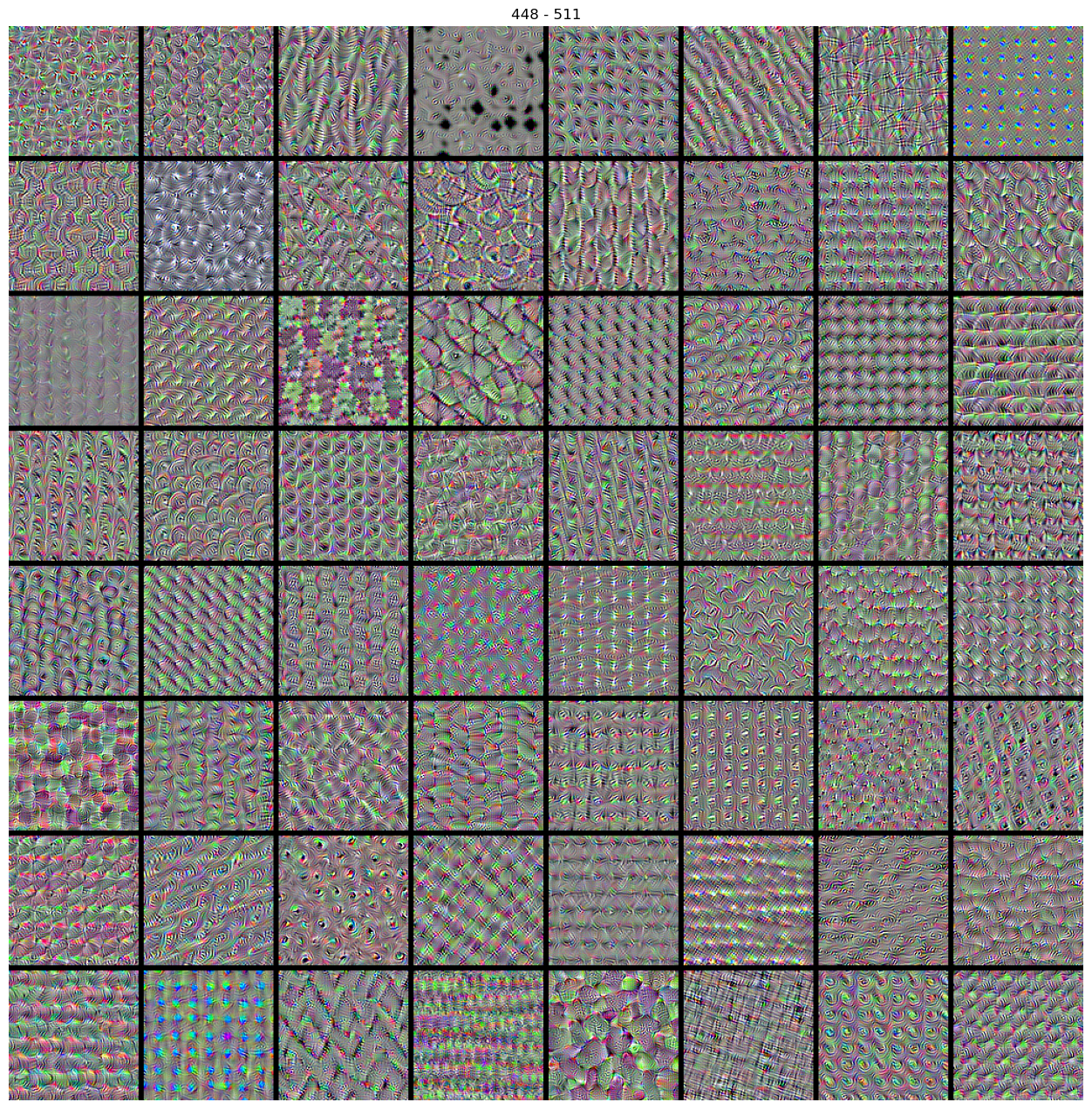
Cálculo de los patrones (imágenes de entrada) que maximizan las activacioens de los 512 filtros de la calpa convolucional de interés.

def compute_nfilters(model=None, f0=0, n=64):
    all_imgs = []
    print("Processing filter: ")
    for filter_index in range(f0,f0+n):
        print(filter_index, end='')
        _, img = visualize_filter(model        = model, 
                                  filter_index = filter_index)
        all_imgs.append(img)   
    return all_imgs

img_filters = compute_nfilters(model=feature_extractor, f0=0, n=512)

Processing filter: 
0......1......2.... ---> ....510......511

len(img_filters)

512

Deplegamos las patrones asociados a cada filtro.

import matplotlib.pyplot as plt

def stitch_filters (img_filters, f0, nn):
    # Build a black picture with enough space for
    # our 8 x 8 filters of size 128 x 128, with a 5px margin in between
    n = int(np.sqrt(nn))
    
    margin = 5
    img_width, img_height ,_= img_filters[0].shape
    cropped_width  = img_width  - 25 * 2
    cropped_height = img_height - 25 * 2
    width  = n * cropped_width  + (n - 1) * margin
    height = n * cropped_height + (n - 1) * margin
    canvas = np.zeros((width, height, 3))
    # Fill the picture with our saved filters
    for i in range(n):
        for j in range(n):
            idx = f0+i * n + j
            img = img_filters[idx]
            canvas[
                (cropped_width  + margin) * i : (cropped_width + margin) * i + cropped_width,
                (cropped_height + margin) * j : (cropped_height + margin) * j
                + cropped_height,
                :,
            ] = img[25:-25,25:-25,:]
            
    plt.figure(figsize=(16,16))
    plt.imshow(canvas)
    plt.axis('off')
    plt.title('{} - {}'.format(f0,f0+n*n-1))
    plt.imsave('img_filters_{}_{}.png'.format(f0,f0+n*n-1),img)

for i in range(512//64):
    stitch_filters(img_filters=img_filters, f0=64*i, nn=8*8)

---

Deep Dream

---

Ahora, en vez de iniciar con una imagen completamente de ruido, usamos una imagen (seleccionamos una aleatoria de internet) y la agregamos ruido, le damos solo unas pocas iteraciones para que a partir de dicha imagen, se le sobrepongan características que maximizan la respuesta de un filtro en particular.

La imagen que decidimos usar como templete es

url = "https://gacetamedica.com/wp-content/uploads/2021/02/GettyImages-1201463812.jpg"
im  = Image.open(requests.get(url, stream=True).raw)
im

De la cual extraemos la parte central y procedemos:

loss, img = visualize_filter(model         = feature_extractor, 
                             filter_index  = 51, 
                             iterations    = 20, 
                             learning_rate = 10.0, 
                             url_img       = url)

import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
plt.imshow(img[25:-25,25:-25,:])
plt.imsave('img_filter.png',img)
plt.axis('off')

Note que los bordes de los rasgos que el filtro coinciden con los bordes de la imagen original.

---

Máxima Activación

---

Entrada que maximiza la respuesta de una clase

De ejemplo usamos la red VGG16 preentrenada con ImageNet, esta vez usamos el modelo completo pues el propósito es calcular:

$$\underset{I}{\mathrm{argmax}} \,\, F(I)_k - \lambda \, \| I \|_2^2$$
donde $F$ representa la red entrenada con Imagenet (VGG16 en nuestro ejemplo). Luego $F(I)_k$ denota la espuesta $k$-ésima de la red, es decir la probabilidad de que la imagen $I$ pertenezca a la clase $k$. Noto que el objetivo es encontrar encontrar la imagen $I$ que maximice la $k$-ésmia entrada en el vector de respuesta de a red $F$. Finalmente, agregamos el regularizador $\| I \|_2^2$; la norma $L_2$ para evitar que la solución óptima $I^*$ se escale sin control. El el parámetro $\lambda$ pondera la contribución (costo, por ello el signo negativo) del regularizador al costo total.

input_shape = (224,224,3)
model_full  = VGG16(weights     = "imagenet", 
                    include_top = True,  
                    input_shape = input_shape,
                    )

Cargamos una imagen aleatoria de interet, que corresponda a alguna clase de ImageNet:

url = "https://gacetamedica.com/wp-content/uploads/2021/02/GettyImages-1201463812.jpg"  #elephant
url = "https://cdn.download.ams.birds.cornell.edu/api/v1/asset/168487331/1800" # archibebe

im  = Image.open(requests.get(url, stream=True).raw)
im = im.resize(input_shape[:2])
img = np.array(im).astype('float32')
img = (img/127.5)-1
img = np.expand_dims(img, 0)
im

Predecimos la clase

preds = model_full.predict(img)

1/1 [==============================] - 0s 23ms/step

preds[:].argmax()

141

Decodificamos el resultado (que clases tienen la mayor probabilidad)

decode_predictions = tf.keras.applications.vgg16.decode_predictions
predictions = decode_predictions(preds, top=3)[0]

print("{:10} {:23} {:12}".format('Id. clase', 'Nombre', 'Probabilidad'))
print(25*' -')
for p in predictions:
        print("{:10s} {:25s} {:0.5}".format(p[0], p[1], p[2]))

Id. clase  Nombre                  Probabilidad
 - - - - - - - - - - - - - - - - - - - - - - - - -
n02028035  redshank                  0.11832
n02033041  dowitcher                 0.093141
n02027492  red-backed_sandpiper      0.056346

Los nombres de todas las clases del modelo se pueden encontrar en: Nombre de las clases. Donde vemos que la clase mas probable corresponde al índice 141 que es un archibebe (redshank).

Con esta información vamos a encotrar la imagen de entrada que maximiza la respuesta de la VGG16 en la clase con índice 141.

LAMBDA = 1e-6
def compute_class_loss(model, input_image, class_index):
    
    preds = model(input_image)
    score =  preds[:, class_index]
    regularizer = tf.nn.l2_loss(input_image)
    
    return score - LAMBDA*regularizer

@tf.function
def class_gradient_ascent_step(model, img, class_index, learning_rate, ):

    with tf.GradientTape() as tape:
        tape.watch(img)
        loss = compute_class_loss(model, img, class_index)

    # calcula gradiente y lo normaliza para evolucion suave de la imagen
    grads = tape.gradient(loss, img)
    grads = tf.math.l2_normalize(grads)
    # ascenso de gradiente
    img += learning_rate * grads
    return loss, img

IMGS=[]
def visualize_class(model=None, class_index=0, iterations=300, learning_rate =10.0, url_img=None):
    
    img = initialize_image()
    for iteration in range(iterations):
        
        loss, img = class_gradient_ascent_step(model, img, class_index, learning_rate)
        
        if iteration%2==0:
            print('.',end ='')
            # decodifica la salida como numpy [0,255]
            im = deprocess_image(img[0].numpy())
            IMGS.append(im)
            
    im = deprocess_image(img[0].numpy())
    return loss, im

loss, img = visualize_class(model         = model_full, 
                            class_index   = 141, 
                            iterations    = 100, 
                            learning_rate = 100.0,
                            )

..................................................

import matplotlib.pyplot as plt
plt.figure(figsize=(8,8))
plt.imshow(img)
plt.axis('off')
plt.imsave('img_class_.png',img)

Ahora, generamos un GIF con las imágenes que fuimos almacenando en la lista IMGS para ver como evoluciona la imagen de entrada que maximiza la activación de la clase seleccionada :

from moviepy.editor import ImageSequenceClip

clip = ImageSequenceClip(IMGS, fps=5)
clip.write_gif('maxization_activation_.gif', fps=5)

MoviePy - Building file maxization_activation.gif with imageio.

El video resultante se muestra a continuación.

Como se puede apreciar, en el centro se va formado la imagen prototipo de un archibebe (confundidos muy comunmente con los tildios). Al mismo tiempo, en otras regiones de la imagen aparecen características propias de los archibebes.