DCGAN: Redes Generadoras Antagónicas Convolucionales Profundas

Deep Convolutional Generative Adversarial Networks (DCGANs)

Código de ejemplo basado en el del Capítulo 3 de Langr and Bok (2019) y en las notas de TensorFlow.Keras.

Mariano Rivera

version 1.0 Febrero 2019
version 2.0 Septiembre 2020

dacgan

El modelo de redes profundas Redes Antagónicas Generadoras (Generative Adversarial Networks, GANs) fué propuesto por Goodfellow et al., 2014b. Las GANs son un modelo generador (de los muchos que existen) que se basa en redes neuronales profundas.

En la sección GAN revisamos los conceptos básicos de una GAN, vimos en los experimentos que si bien las imágenes generadas son mas contrastadas que las producidas por una Autocodificadores Variacionales (VAEs), las imágenes no eran de buenan calidad.

En esta sección reformularemos el modelo de la GAN basadas en Perceptrones Multicapa a Convolucionales (Radford and Metz, 2015). La siguiente figura ilustra (a manera de recordatorio) la arquitectura de una red convolucional. Detalles de implementación en Keras pueden encontrarse en Dumoulin and Visin (2016), notas convnets 1, notes convnets 2 y Chollet (2018)

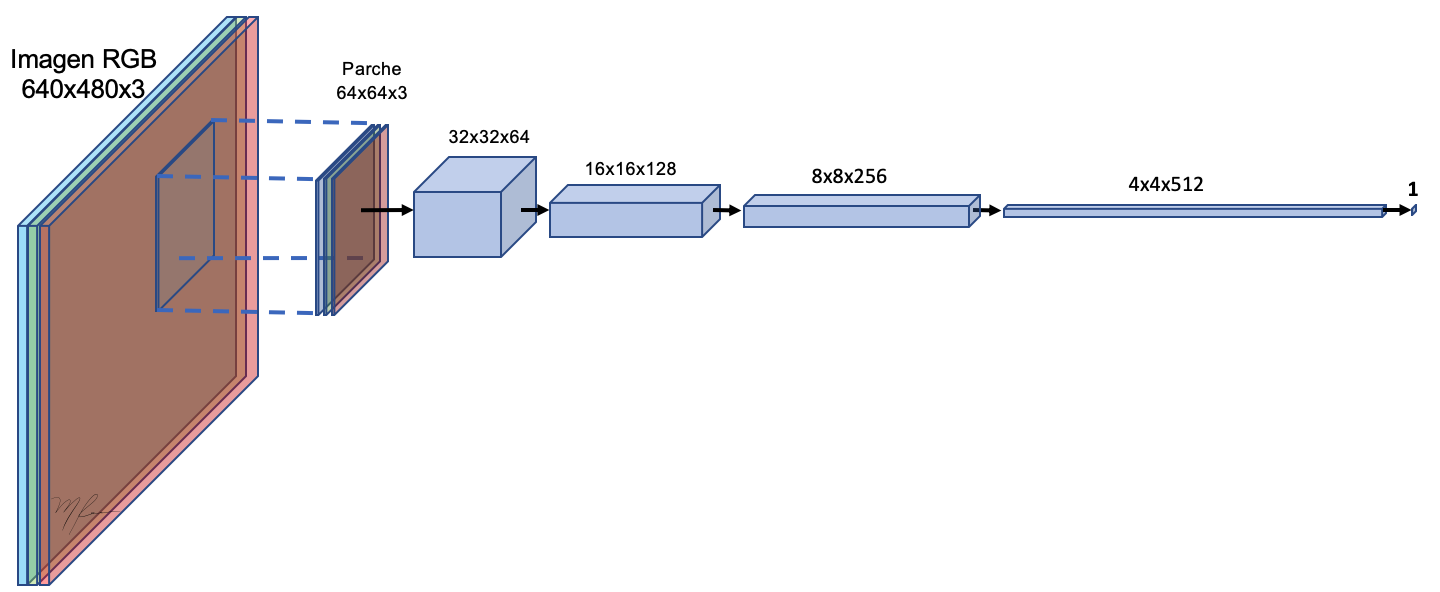
conv2d

El nuevo modelo GAN lo denominaremos Redes Generadoras Antagónicas Convolucionales Profundas (DCGANs).

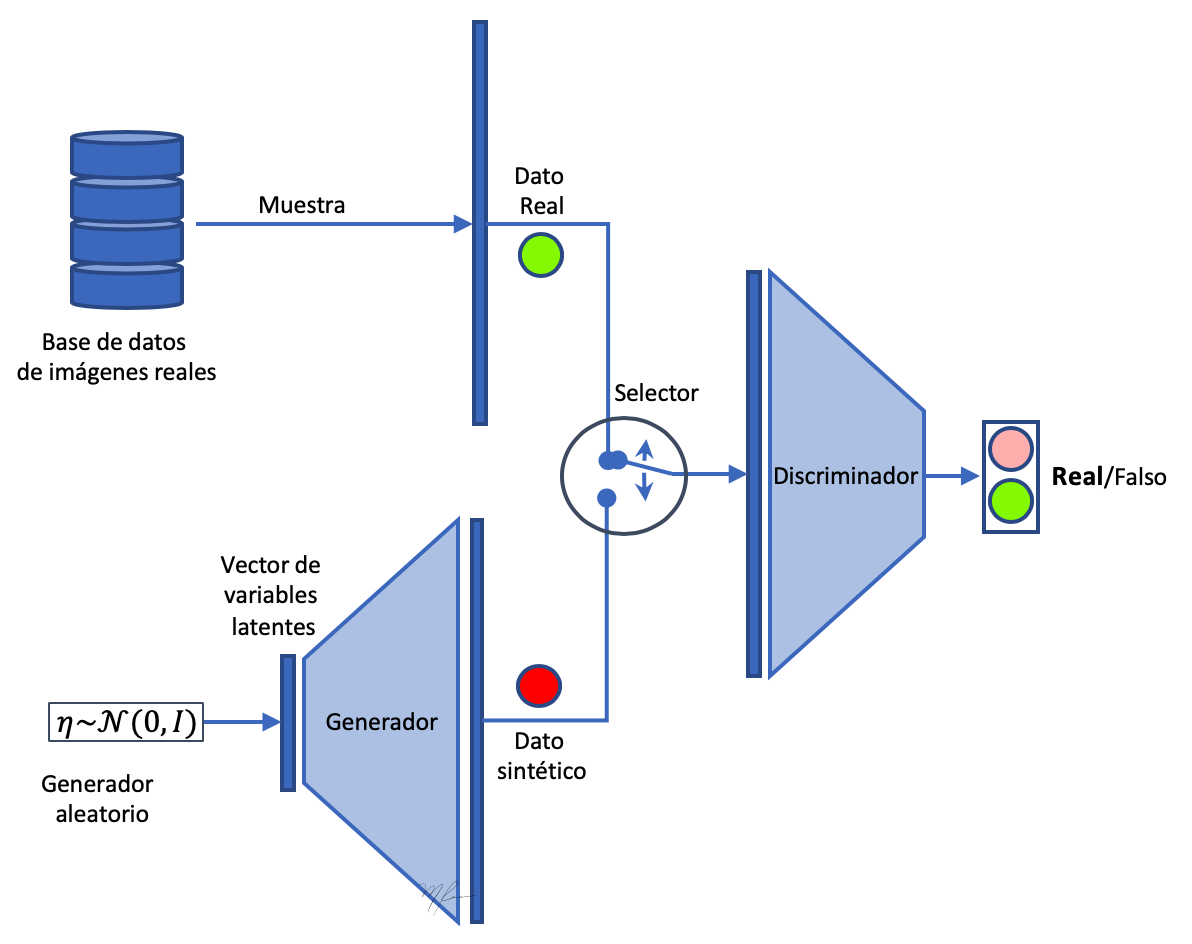
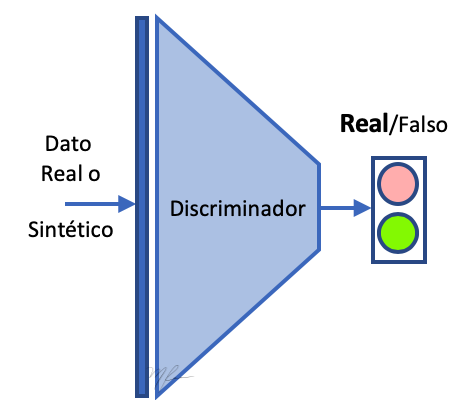
El modelo general seguirá siendo el de una GAN: un generador y un discriminador. El propósito del Generador GG es generar datos sintéticos x~\tilde x que sean indistinguibles de los datos reales para el Discriminador DD. Por lo que el discriminador es una red que clasifica datos que se le presentan entre reales o falsos (fakes). La siguiente figura representa una GAN.

gan

Función Objetivo de la GAN

Sean y∈{0,1}y \in \{0,1\} la etiqueta del dato xx correspondientes a “falso” o “real” y y^∈[0,1]\hat y \in [0,1] su estimación obtenida del discriminador para el dato en cuestión. Luego, la función a optimizar mediante el entrenamiento de la GAN esta dada por la cross entropía binaria:

(1)
J(y^;y)=−∑i[yilog⁡y^i+(1−yi)log⁡(1−y^i)] J(\hat y; y) = - \sum_{i} \left[ y_i \log \hat y_i + (1-y_i)\log (1-\hat y_i) \right]

pero la clasificación y^\hat y puede obtenerse a partir de un dato real xx o de uno falso x(z)x(z). Separando los casos de y=1y=1 para datos reales y y=0y=0 para datos falsos, el probema de optimización nos queda como

(2)
max⁡θdmin⁡θg−∑x∈datalog⁡y^i(x,θd)−∑z∼pg(z)log⁡[1−y^i(z,θd,θg)] \underset{\theta_d}{\max} \underset{\theta_g}{\min} - \sum_{x \in data} \log \hat y_i(x, \theta_d) - \sum_{z \sim p_g(z)} \log [1-\hat y_i(z, \theta_d, \theta_g)]

donde

Ahora, sean DD y GG las redes representacionales del discriminador y generador, respectivamente; entonces, de acuerdo a Goodfellow (2016b), la función de pédida (2) se reescribe como

(3)
min⁡θdmax⁡θg−∑x∈datalog⁡D(x;θd)−∑z∼pg(z)log⁡[1−D(G(z;θg);θd)] \underset{\theta_d}{\min} \underset{\theta_g}{\max} - \sum_{x \in data} \log D(x;\theta_d) - \sum_{z \sim p_g(z)} \log [1-D(G(z; \theta_g);\theta_d)]

Note que la optimización del Generador intentará encontrar parámetros que confundan al Discriminador: que etiqueten datos falsos como reales, con y^(z)≈1\hat y(z) \approx 1. Luego −log⁡[1−D(G(z;θg);θd)]>>0- \log [1-D(G(z; \theta_g);\theta_d)] >> 0, lo que es conveniente para maximizar la función de pérdida respecto al generador.

Estrategia de entrenamiento de la GAN

A continuación damos el esquema general a seguir para entrenar una GAN.

for t in n-Iterations:

end for

Normalización de Lotes (Batch Normalization)

La normalización del por lotes fué propuesta por Ioffe and Szegedy (2015). Se implementa como sigue. Sean, respectivamente, μB\mu_B la media y σB\sigma_B desviación estándard del lote calculadas como

(4)
μB=1m∑kz(k) \mu_B = \frac{1}{m} \sum_{k} z^{(k)}

y

(5)
σB2=1m∑k(z(k)−μB)2 \sigma_B^2 = \frac{1}{m} \sum_{k} (z^{(k)}- \mu_B)^2

La normalización por lote de un vector consiste en restar a cada entrada la media y dividirla entre desviación estándard del lote. Al re-escalar las entradas, hacemos menos sensible el entrenamiento a las escalas de las características de entrada. La implementación de la normalización por lote consiste en

(6)
z(k)=z(k)−μBσB2+ϵ z^{(k)} = \frac{ z^{(k)} - \mu_{B} }{\sqrt{\sigma^2_{B} + \epsilon}}

donde μB\mu_{B} es el vector de medias sobre el lote, σB2\sigma^2_{B} es un vector de desviaciones estándares del lote y ϵ\epsilon es una constante pequeña que evita la división por cero.

Una vez que la entrada es normalizada con (6), esta es reescalada y recorrida usando los escalares γ\gamma y β\beta que son ajustados durante el proceso de entrenamiento:

(7)
y(k)=γz(k)+β y^{(k)} = \gamma z^{(k)} + \beta

valor que es pasado a la siguiente capa de la red. Los parámetros γ\gamma y β\beta son aprendidos durante el proceso de entrenamiento.

En keras, la normalización por lote se realiza mediate la capa keras.layers.BatchNormalization.

Referencias

(Langr & Bok, 2019) Jakub Langr and Vladimir Bok, GANs in Action, MEAP Ed. Manning Publications Co, 2019.

(Goodfellow et al., 2014b) Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014b). Generative adversarial net- works. In NIPS’2014. arXiv:1406.2661

(Goodfellow et al., 2016a) Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT Press. http://www.deeplearningbook.org.

(Goodfellow, 2016b) Ian Goodfellow, NIPS 2016 Tutorial: Generative Adversarial Networks, arXiv:1701.00160, 2016.

(Dumoulin and Visin, 2016) Vincent Dumoulin and Francesco Visin. A guide to convolution arithmetic for deep learning, 2016; arXiv:1603.07285.

(Chollet, 2018) François Chollet, Deep Learning with Python, Manning Publications Co, 2018.

(Radford and Metz, 2015) Alec Radford and Luke Metz: “Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks”, 2015; arXiv:1511.06434.

(Ioffe and Szegedy, 2015) Sergey Ioffe and Christian Szegedy: “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”, 2015; arXiv:1502.03167.

Código de DCGAN básica

import os
os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID";
os.environ["CUDA_VISIBLE_DEVICES"]="0";

import tensorflow as tf
if tf.test.gpu_device_name():
    print('Default GPU Device: {}'.format(tf.test.gpu_device_name()))
else:
    print("Please install GPU version of TF")

Default GPU Device: /device:GPU:0

import sys
import numpy as np
import matplotlib.pyplot as plt

from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Input, Dense, Reshape, Flatten, Dropout
from tensorflow.keras.layers import BatchNormalization, ZeroPadding2D
from tensorflow.keras.layers import Activation, LeakyReLU
from tensorflow.keras.layers import Conv2D, Conv2DTranspose

from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.optimizers import Adam

def reset_weights(model):
    '''
    Reinicializa los pesos del modelo 
    '''
    for ix, layer in enumerate(model.layers):
        if hasattr(model.layers[ix], 'kernel_initializer') and \
                hasattr(model.layers[ix], 'bias_initializer'):
            weight_initializer = model.layers[ix].kernel_initializer
            bias_initializer   = model.layers[ix].bias_initializer

            old_weights, old_biases = model.layers[ix].get_weights()

            model.layers[ix].set_weights([
                weight_initializer(shape=old_weights.shape),
                bias_initializer  (shape  =len(old_biases))])

Parámetros generales

Lee los datos reales y pone variables globales

# carga datos reales     
(X_train, _), (_, _) = mnist.load_data()

# Rescale -1 to 1
X_train = X_train / 127.5 - 1.
X_train = np.expand_dims(X_train, axis=3)

Variables globales

(buffer_size,img_rows, img_cols, channels) = X_train.shape
img_shape  = (img_rows, img_cols, channels)
z_dim      = 20     # dimensión del espacio latente
batch_size = 256
num_epochs = 100
each_save  = 5

path_results = 'dcgan_results/'

Iterador sobre el conjunto de entrenamiento por lotes

train_dataset = tf.data.Dataset.from_tensor_slices(X_train).shuffle(buffer_size).batch(batch_size)
train_dataset

<BatchDataset shapes: (None, 28, 28, 1), types: tf.float64>

Generador

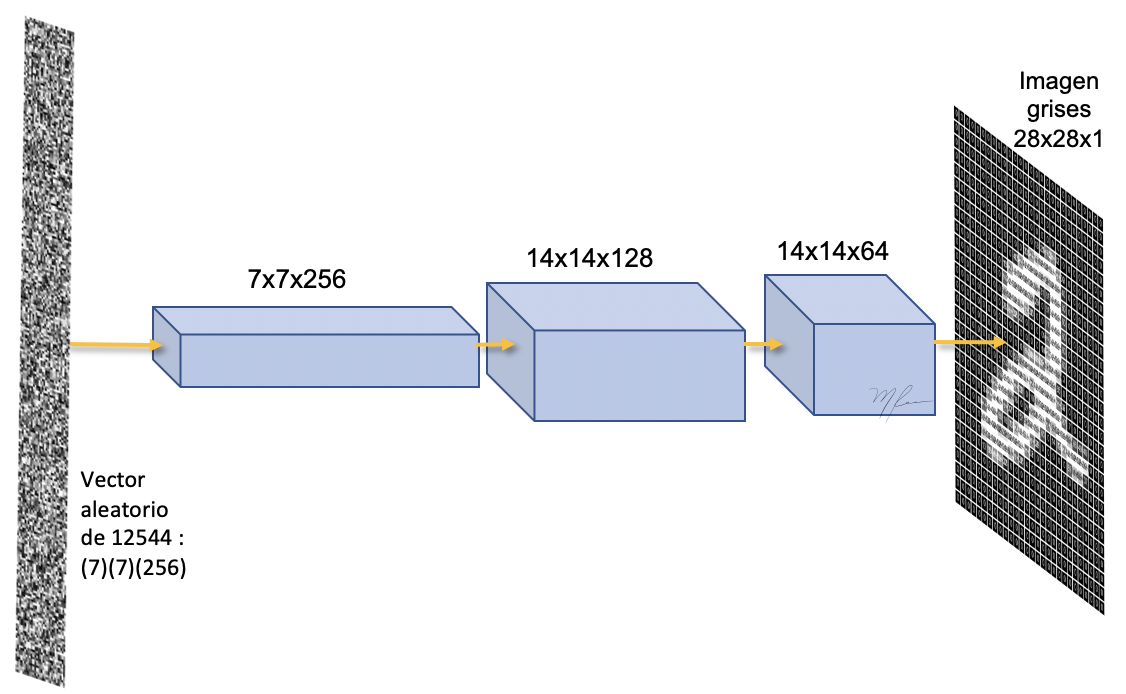
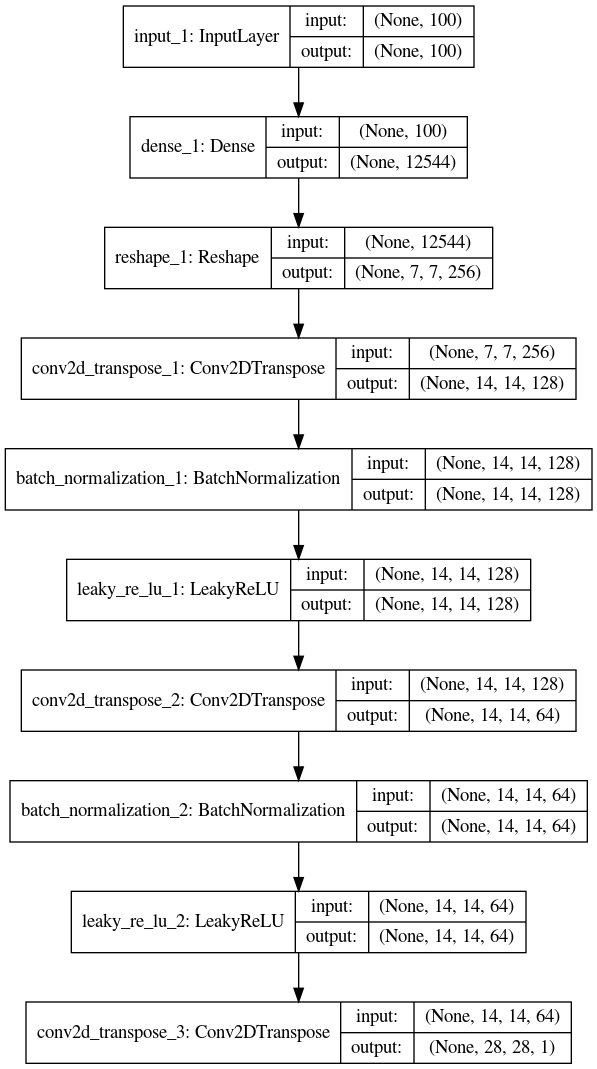
En generador es una red convolucional que

  1. Toma como entrada un vector aleatorio de 2020 entradas

  2. El cuál es pasado por una capa densa de dimensiones (7)(7)(256)(7)(7)(256) y luego reformateado (reshape) a un tensor de forma 7×7×2567 \times 7 \times 256.

  3. Luego es pasado a una convolución transpuesta que convierte el tensor 7×7×2567 \times 7 \times 256 en uno de 14×14×12814 \times 14 \times 128. Con posterior normalización or lotes y actrivación ReLU.

  4. Luego es pasado a una convolución transpuesta que convierte el tensor 14×14×12814 \times 14 \times 128 en uno de 14×14×6414 \times 14 \times 64. Con posterior normalización or lotes y actrivación ReLU.

  5. Y de nuevo usando una convolución transpuesta se transforma el tensor 14×14×6414 \times 14 \times 64 en uno del tamaño de la imagen de salida 28×28×128 \times 28 \times 1 a la que se la aplica una activación tanh

Esto se ilustra en la siguiente figura.

dcgan_generador

from tensorflow.keras.utils import plot_model

def build_generator(img_shape, z_dim, verbose=False):
    '''
    Genera una imagen de 28x28x1 a partir de un vector aleatorio de 100 entradas (espacio latente)
    '''

    z = Input(shape=(z_dim,))

    # Pasa entrada unidimensional de dimensión 20 en un tensor de (7)(7)(256) tensor via un red Densa
    # luego la reformatea en un tensor de 7x7x128
    X = Dense(256 * 7 * 7, input_dim=z_dim) (z)
    X = Reshape((7, 7, 256))(X)

    # Convolución transpuesta, tensor de 7x7x256 a 14x14x128, con normalización por lote y activación ReLU
    X = Conv2DTranspose(filters    =128, 
                        kernel_size=3, 
                        strides    =2, 
                        padding    ='same')(X)
    X = BatchNormalization()(X)
    X = LeakyReLU(alpha=0.01)(X)
    
    # Convolución transpuesta, tensor de 14x14x128, a 14x14x64 con normalización por lote y activación ReLU
    X = Conv2DTranspose(filters    =64, 
                        kernel_size=3, 
                        strides    =1, 
                        padding    ='same')(X)
    X = BatchNormalization()(X)
    X = LeakyReLU(alpha=0.01)(X)
    
    # Convolución transpuesta, tensor de 14x14x128 a 28x28x1, con activación tahn
    Y = Conv2DTranspose(filters    =1, 
                        kernel_size=3, 
                        strides    =2, 
                        padding    ='same',
                        activation ='tanh')(X)
    
    generator_model = Model(inputs = z, outputs = [Y], name ='generator')
    
    return generator_model

Construye Generador

generator = build_generator(img_shape, z_dim)
generator.summary()

Model: "generator"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         [(None, 20)]              0         
_________________________________________________________________
dense (Dense)                (None, 12544)             263424    
_________________________________________________________________
reshape (Reshape)            (None, 7, 7, 256)         0         
_________________________________________________________________
conv2d_transpose (Conv2DTran (None, 14, 14, 128)       295040    
_________________________________________________________________
batch_normalization (BatchNo (None, 14, 14, 128)       512       
_________________________________________________________________
leaky_re_lu (LeakyReLU)      (None, 14, 14, 128)       0         
_________________________________________________________________
conv2d_transpose_1 (Conv2DTr (None, 14, 14, 64)        73792     
_________________________________________________________________
batch_normalization_1 (Batch (None, 14, 14, 64)        256       
_________________________________________________________________
leaky_re_lu_1 (LeakyReLU)    (None, 14, 14, 64)        0         
_________________________________________________________________
conv2d_transpose_2 (Conv2DTr (None, 28, 28, 1)         577       
=================================================================
Total params: 633,601
Trainable params: 633,217
Non-trainable params: 384
_________________________________________________________________

generador

Discriminador

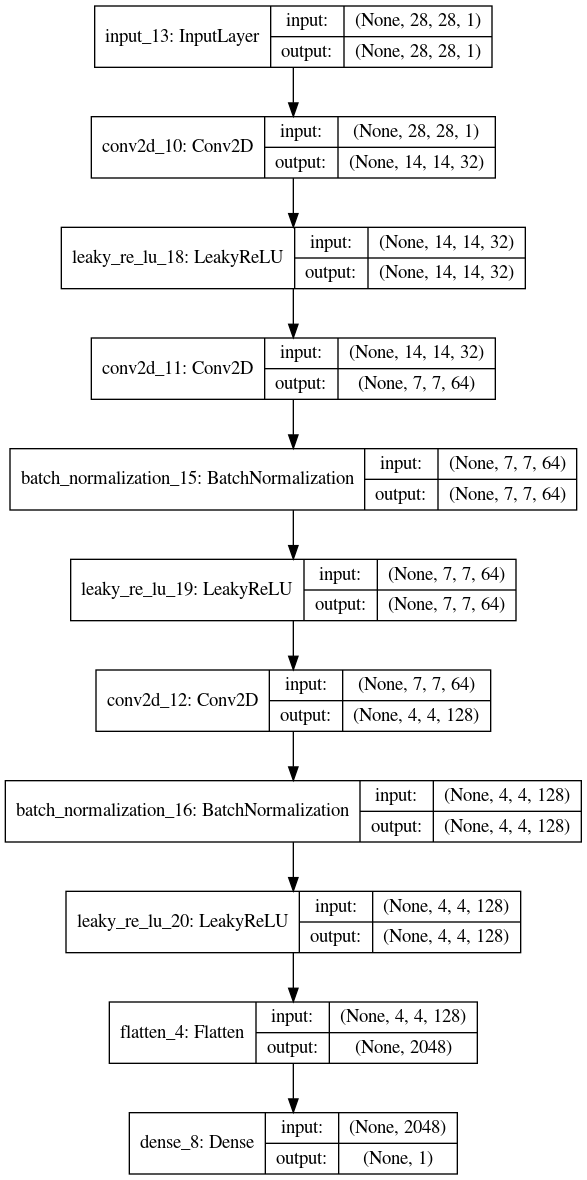
En discriminador es una red neuronal secuencial profunda que recibe de entrada un vector datos y produce una clasificación indicando si los datos son reales o falsos (fake).

discriminador

def build_discriminator(img_shape, verbose=False):

    Xin = Input(shape=(img_shape[0],img_shape[1],img_shape[2],))

    # Convolución2D tensor de 28x28x1 a 14x14x32 y activación Leaky ReLU
    X = Conv2D(filters     = 32, 
               kernel_size = 3, 
               strides     = 2, 
               input_shape = img_shape, 
               padding     = 'same')(Xin)
    #X = BatchNormalization()(X)
    X = LeakyReLU(alpha    = 0.01)(X)

    # Convolución2D tensor de 14x14x32 a 7x7x64, con normalización por lote y activación Leaky ReLU
    X = Conv2D(filters     = 64, 
               kernel_size = 3, 
               strides     = 2, 
               padding     = 'same')(X)
    X = BatchNormalization()(X)
    X = LeakyReLU(alpha    = 0.01)(X)
    
    # Convolución2D tensor de 7x7x64 a 3x3x128, con normalización por lote y activación Leaky ReLU
    X = Conv2D(filters     = 128, 
               kernel_size = 3, 
               strides     = 2,  
               padding     = 'same')(X)
    X = BatchNormalization()(X)
    X = LeakyReLU(alpha    = 0.01)(X)

    # Aplanado del tensor, y capa densa de salida de clasificacion con activación sigmoide
    X = Flatten()(X)
    Yout = Dense(1, activation='sigmoid')(X)

    discriminator_model = Model(inputs = Xin, outputs = [Yout], name ='discriminator')

    return discriminator_model

Construye y compila el Discriminador

# construye el discriminador 
discriminator = build_discriminator(img_shape)
discriminator.summary()

Model: "discriminator"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_2 (InputLayer)         [(None, 28, 28, 1)]       0         
_________________________________________________________________
conv2d (Conv2D)              (None, 14, 14, 32)        320       
_________________________________________________________________
leaky_re_lu_2 (LeakyReLU)    (None, 14, 14, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 7, 7, 64)          18496     
_________________________________________________________________
batch_normalization_2 (Batch (None, 7, 7, 64)          256       
_________________________________________________________________
leaky_re_lu_3 (LeakyReLU)    (None, 7, 7, 64)          0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 4, 4, 128)         73856     
_________________________________________________________________
batch_normalization_3 (Batch (None, 4, 4, 128)         512       
_________________________________________________________________
leaky_re_lu_4 (LeakyReLU)    (None, 4, 4, 128)         0         
_________________________________________________________________
flatten (Flatten)            (None, 2048)              0         
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 2049      
=================================================================
Total params: 95,489
Trainable params: 95,105
Non-trainable params: 384
_________________________________________________________________

discriminator

Funciones de Pérdida

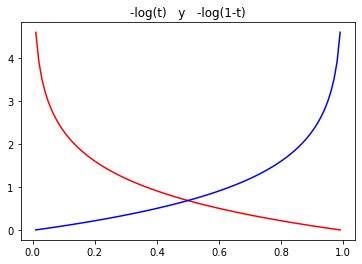
Basadas en la cross-entropía:

(10)
−∑iyilog⁡y^i=−∑i:yi=1log⁡y^i−∑i:yi=0log⁡(1−y^i) -\sum_i y_i \log \hat y_i = -\sum_{i:y_i=1} \log \hat y_i - \sum_{i:y_i=0} \log (1- \hat y_i)

dado que yi{0,1}y_i \{0,1 \}: el dato o es sintético, o es verdadero.

n=100
t = np.arange(1,n)/n
plt.plot(t,-np.log(t), 'r')
plt.plot(t,-np.log(1-t), 'b')
plt.title('-log(t)   y   -log(1-t)')
plt.show()

png

cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)

Pérdida del Discriminador

La función de pérdida del Discriminador son los errores de las predicciones de los datos verdaderos y de los sintéticos:

(11)
JD=−∑i:yi=1log⁡y^i−∑i:yi=0log⁡(1−y^i) J^D = -\sum_{i:y_i=1} \log \hat y_i - \sum_{i:y_i=0} \log (1- \hat y_i) 

def discriminator_loss_classic(real_output, fake_output):
    # pérdida de los verdaeros (1 vs y_hat )
    real_loss = cross_entropy(tf.ones_like(real_output), real_output)
    # pérdida de los sintéticos (0 vs y_hat )
    fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output)
    # suma de los dos tipos de errores
    total_loss = real_loss + fake_loss
    return total_loss

def discriminator_loss(real_output, fake_output):
    # pérdida de los verdaeros (1 vs y_hat )   + pérdida de los sintéticos (0 vs y_hat 
    total_loss = -tf.reduce_mean(tf.keras.backend.log(real_output) + tf.keras.backend.log(1.- fake_output))
    return total_loss

Note que en el la definición de la función pasada hemos usado cross_entropypara cada etiqueta aunque sabemos de antemano que sólo una de las sumasse estará evaluando. Sin embargo esto simplifica nuestra implementación.

Pérdida del Generador

La función de pérdida del Generador deberá promover el predecir datos sintéticos como verdaderos (maximizar los Falsos Positivos):

(12)
JG=−∑i:yi=0log⁡y^i J^G = - \sum_{i:y_i=0} \log \hat y_i

Por lo que usamos la cross-entropía con la etiqueta cambiada para implementarla.

def generator_loss_classic(fake_output):
    return cross_entropy(tf.ones_like(fake_output), fake_output)

def generator_loss(real_output,fake_output):
    #  pérdida de los sintéticos (0 vs y_hat 
    total_loss = -tf.reduce_mean(tf.keras.backend.log(fake_output))
    return total_loss

Optimizadores para los modelos

Usaremos ADAM para ambos modelos.

generator_optimizer     = tf.keras.optimizers.Adam(1e-5)
discriminator_optimizer = tf.keras.optimizers.Adam(1e-5)

Paso de entrenamiento

Definiremos un paso de entrenamiento de la GAN, que corresponde a hacre un paso de entrenamiento en cada modelo.

  1. Carga lote de imágenes reales XX

  2. Genera un lote de variables latentes ZZ

  3. Genera un lote de variables sintéticas: X^=G(Z;θg)\hat X = G(Z; \theta_g)

  4. Calcula las predicciones para Y^=D([X∣X^],θd)\hat Y = D([X | \hat X], \theta_d)

  5. Calcula costos JDJ^D y JGJ^G.

  6. Calcula gradientes ∇θdJD\nabla_{\theta_d} J^D y ∇θgJG\nabla_{\theta_g} J^G.

  7. Actualiza pesos con un paso del algoritmo de optimización:

θd=θd+δ(∇θdJD)θg=θg+δ(∇θgJG) \theta_d = \theta_d + \delta(\nabla_{\theta_d} J^D) \\ \theta_g = \theta_g + \delta(\nabla_{\theta_g} J^G) \\
donde δ(⋅)\delta(\cdot) representa el paso del algoritmo utilizado.

#El decorador `tf.function` indica que la función se "compila" para que pueda incluirse en un gráfo de calculo.

@tf.function
def train_step(images):
    '''
    
    Implementa un paso de entrenamiento para la GAN
    
    Recibe como parámetros un semi-lote de imágenes reales
    '''

    # variables latentes (ruido Gaussiano), tantas como imagenes reales
    z = tf.random.normal([images.shape[0], z_dim])

    # Los siguientes pasos registaran (en "TAPE") para efectos de calcular gradientes
    # son dos "Tapes" para registrar los calculos de cada modelo
    with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
        
        # genera el semi-lote de datos sintéticos
        generated_images = generator(z, training=True)
        
        # calcula la predicción para datos verdaderos y falsos
        real_output = discriminator(images, training=True)
        fake_output = discriminator(generated_images, training=True)

        # calcula las pérdidas del Discriminador y del Generador
        disc_loss = discriminator_loss(real_output, fake_output)
        gen_loss  = generator_loss(real_output, fake_output)

    # Para cada modelo, calcula el gradiente de su función de costo respecto a sus pesos entrenables, 
    # haciendo retropropagación sobre los calculos realizados
    gradients_of_generator     = gen_tape.gradient(gen_loss, generator.trainable_variables)
    gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)

    # Hace el paso de actualizacion de los pesos
    generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
    discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))
    
    return gen_loss, disc_loss

Iteración del entrenamiento

from PIL import Image
import imageio
import glob

# - - - - - - - - - - - - - - - - - - - - - - - - - - 
# Crea una collage de imágenes con el Generador y la guarda
# - - - - - - - - - - - - - - - - - - - - - - - - - - 

num_examples_to_generate = 16 # (4,4)
seed = tf.random.normal([num_examples_to_generate, z_dim])

def generate_and_save_images(model, epoch, test_input, pathdir=path_results):
    # Se pone entrenable en Falso porque esta en modo inferencia el 
    predictions = model(test_input, training=False)

    fig = plt.figure(figsize=(4,4))  

    for i in range(predictions.shape[0]):
        plt.subplot(4, 4, i+1)
        plt.imshow(predictions[i, :, :, 0] * 127.5 + 127.5, cmap='gray')
        plt.axis('off')

    plt.savefig(pathdir+'image_epch_{:04d}.png'.format(epoch))
    plt.show()
    
# - - - - - - - - - - - - - - - - - - - - - - - - - - 
# Despliega la imagen correspondiente a una época
# - - - - - - - - - - - - - - - - - - - - - - - - - - 

def display_image(epoch_no, pathdir=path_results):
    return Image.open(pathdir+'image_epch_{:04d}.png'.format(epoch_no))


from IPython import display
import time 

def train(dataset, epochs):
    
    generator_losses=[] 
    discriminator_losses=[]
    for epoch in range(epochs):
        start = time.time()

        for image_batch in dataset:
            gen_loss, disc_loss = train_step(image_batch)

        # solo registramos los costos en el último lote
        generator_losses.append(gen_loss)
        discriminator_losses.append(disc_loss)
        
        # Produce imágenes para crear el GIF
        if (epoch+1)%each_save ==0:
            display.clear_output(wait=True)  # limpia el buffer
            generate_and_save_images(generator,
                                     epoch + 1,
                                     seed)
        
        print ('Time for epoch {} is {} sec'.format(epoch + 1, time.time()-start))

    # Genera las las imágens correspondientes a la época final
    display.clear_output(wait=True)
    generate_and_save_images(generator,
                               epochs,
                               seed)
    
    return np.array(generator_losses), np.array(discriminator_losses)

Entrenamiento de la GAN

generator_losses, discriminator_losses = train(train_dataset, num_epochs)

png

display_image(num_epochs)

png

Salvar modelos y graficar desempeño

generator.save_weights('dcgan_generator_0_1.h5')
discriminator.save_weights('dcgan_discriminator_0_1.h5')

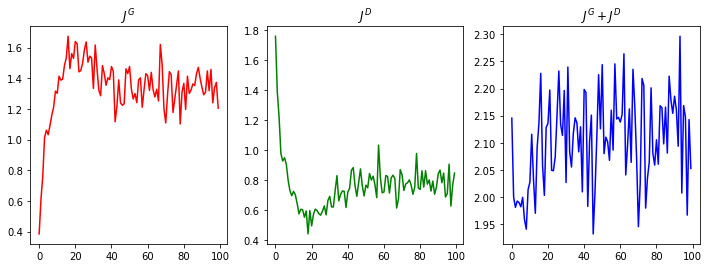
plt.figure(figsize=(12,4))
plt.subplot(131)
plt.plot(generator_losses, 'r')
plt.title('$J^G$')
plt.subplot(132)
plt.plot(discriminator_losses, 'g')
plt.title('$J^D$')
plt.subplot(133)
plt.plot(generator_losses+discriminator_losses, 'b')
plt.title('$J^G+J^D$')
plt.show()

png