Red Convolucional con Base de Datos Pequeñas

Mariano Rivera

septiembre 2018

Ejemplo Basado en el del Capítulo 5, Sección 2 del libro Deep Learning with Python

import keras
keras.__version__

Using TensorFlow backend.

'2.2.4'

La eficiencia de las DNN es proporcional al tamaño y variabilidad de la base de datos con que se entrenan.

En ocasiones, contar con una gran DB en tareas de procesamiento de imágenes o visión por computadora es un problema y se tienen que proceder con DB pequeñas.

En este ejemplo se usan una porción de la conocida DB perros y gatos (‘dogs and cats’) con las siguientes dimensiones

Imágenes

2000 gatos
2000 perros

y se usarán

2000 (1000/1000) para entrenamiento
1000 (500/500) validación
1000 (500/500) para evaluación

Cuando se tienen pocos datos y un modelos con muchos parámetros se induce un sobreajuste (over-fitting) del modelos a los datos (se hace un muy buen ajuste del los datos de entrenamiento) y se tiende a tener un mal desempeño en el conjunto de evaluación. Como cuando hacemos regresión mediante mínimos cuadrados a pocos datos ( $m$ ) con un modelo polinomial de orden mayor ( $n$ ); $n>m$ . Lo que ocurre es que el polinomio reproduce muy bien los datos, pero es malo para predecir datos no usados en el entrenamiento (datos no observados en el entrenamiento). La siguiente figura ilustra como el sobreajuste se transforma en una baja capacidad de predicción de datos no observados (se tienen poca capacidad de generalización).

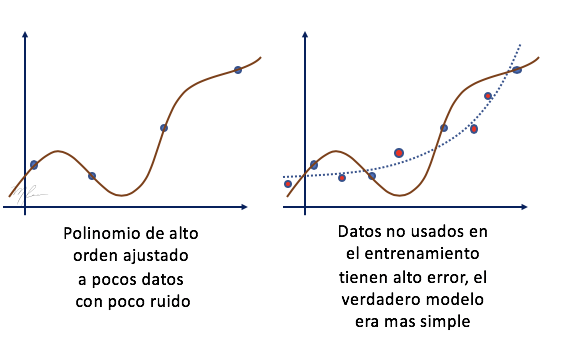
regresion

En el caso de imágenes, una forma de incrementar (aumentar, data augmentation) la DB es introducir variaciones en las imágenes tal que el resultado siga siendo realista.

Las imágenes con las que trabajaremos son como las siguientes

perro1

perro2

perro3

perro4

Como podemos observar, transformaciones válidas pueden ser:

Reflexión vertical. Definida por una variable aleatoria booleana.
Rotaciones pequeñas. Definida por un ángulo de rotación aleatorio en el intervalo $[\theta_h, \theta_h]$ .
Cambio a escala menor o mayor (zoom-in, zoom-out). Definido por el factor de amplificación en el intervalo $[-z, z]$ .

Como estrategia usaremos generadores (generators) en vez de aplicar la transformación y almacenar en disco el conjunto grande de datos transformados: se aplicarán al vuelo las transformaciones a las imágenes; es decir,
como las vayamos utilizando.

Los generators nos permiten aplicar transformaciones aleatorias: los parámetros de las transformaciones son también generados conforme se usan las imágenes en el entrenamiento.

La base de datos completa se puede obtener de Kaggle: https://www.kaggle.com/c/dogs-vs-cats/data; donde el problema de clasificar imágenes de perros y gatos fue originalmente planteado.

La base de datos original contiene 25,000 imágenes: 12,500 de perros y 12,500 de gatos. Aquí usaremos un subconjunto de dicha DB.

Comprobando que la DB este en los directorios adecuados

import os, shutil

try:
    # Directorio con la DB pequeña
    base_dir = '/home/mariano/Documents/deep/kaggle/dogs_vs_cats_small'
    os.stat(base_dir)

    # Directorios de entrenamiento
    # validacion y evaluacion 
    train_dir = os.path.join(base_dir, 'train')
    os.stat(train_dir)
    validation_dir = os.path.join(base_dir, 'validation')
    os.stat(validation_dir)
    test_dir = os.path.join(base_dir, 'test')
    os.stat(test_dir)
    
    # Directorio entrenamiento de gatos (1000 imgs)
    train_cats_dir = os.path.join(train_dir, 'cats')
    os.stat(train_cats_dir)
    
    # Directorio entrenamiento de perros (1000 imgs)
    train_dogs_dir = os.path.join(train_dir, 'dogs')
    os.stat(train_dogs_dir)
    
    # Directorio validacion de gatos (500 imgs)
    validation_cats_dir = os.path.join(validation_dir, 'cats')
    os.stat(validation_cats_dir)
    
    # Directorio validacion de perros (500 imgs)
    validation_dogs_dir = os.path.join(validation_dir, 'dogs')
    os.stat(validation_dogs_dir)
    
    # Directorio validacion de gatos (500 imgs)
    test_cats_dir = os.path.join(test_dir, 'cats')
    os.stat(test_cats_dir)
    
    # Directorio validacion de perros (500 imgs)
    test_dogs_dir = os.path.join(test_dir, 'dogs')
    os.stat(test_dogs_dir)
        
    print('Estructura de directorios completa')
    
except:
    print('Estructura de directorios incompleta')

Estructura de directorios completa

Comprobamos el tamaño de cada subconjunto

print('total training cat images:', len(os.listdir(train_cats_dir)))

total training cat images: 1000

print('total training dog images:', len(os.listdir(train_dogs_dir)))

total training dog images: 1000

print('total validation cat images:', len(os.listdir(validation_cats_dir)))

total validation cat images: 500

print('total validation dog images:', len(os.listdir(validation_dogs_dir)))

total validation dog images: 500

print('total test cat images:', len(os.listdir(test_cats_dir)))

total test cat images: 500

print('total test dog images:', len(os.listdir(test_dogs_dir)))

total test dog images: 500

Arquitectura de la NN

Procederemos como en el caso de clasificación de la de la DB MNIST: con una red convolucional de dos etapas:

extracción de características y
etapa de clasificación.

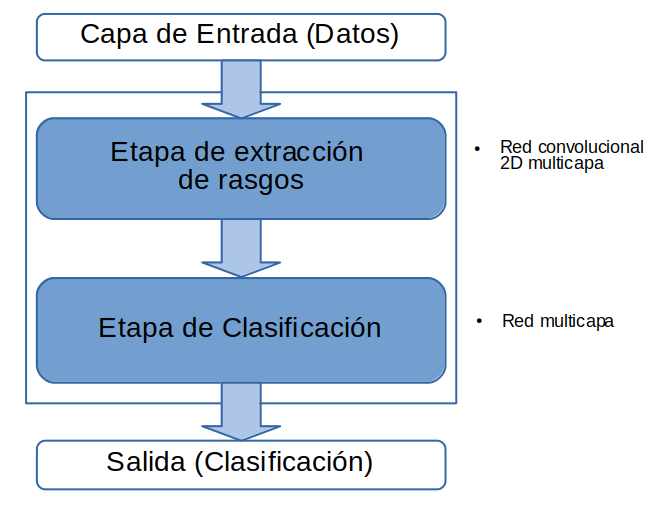
dos_etapas

Etapa de Extracción de Características

La etapa de extracción de características la construiremos usando capas Conv2D (de $3 \times 3$ con activación relu ) alternadas con capas MaxPooling de $2 \times 2$ .

A diferencia de MNIST donde todas las imágenes son de dimensiones $28 \times 28$ , en Cats-and-Dogs las dimensiones son muy variadas. Así que se pondrán todas las imágenes a una dimensión uniforme $150 \times 150$ . Esto nos lleva al siguiente punto, si en cada par de capas Conv2D-MaxPooling, la imagen de entrada reduce sus dimensiones en poco menos que la mitad (por efecto no usar padding para ampliar bordes en la Conv2D) y queremos concluir con un número relativamente pequeño de rasgos (digamos dimensiones espaciales de $7 \times 7$ ), entonces requerimos usar mas bloques Conv2D-MaxPooling

from keras import layers
from keras import models

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
                        input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))

Etapa de Clasificación

La etapa de clasificación inicia con una layer Flatten para poner el tensor resultante de la etapa de extracción de características en forma de vector unidimensional. Luego usaremos una capas tipo Dense con activación relu y concluiremos con una capa de una neurona para hacer la clasificiación binaria con activación sigmoid que codifica la probabilidad de que la imágen analizada pertenezca a la clase 1.

model.add(layers.Flatten())
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

Resumen de la NN

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 148, 148, 32)      896       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 74, 74, 32)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 72, 72, 64)        18496     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 36, 36, 64)        0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 34, 34, 128)       73856     
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 17, 17, 128)       0         
_________________________________________________________________
conv2d_4 (Conv2D)            (None, 15, 15, 128)       147584    
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 7, 7, 128)         0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 6272)              0         
_________________________________________________________________
dense_1 (Dense)              (None, 512)               3211776   
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 513       
=================================================================
Total params: 3,453,121
Trainable params: 3,453,121
Non-trainable params: 0
_________________________________________________________________

Parámetros de Entrenamiento

Los parámetros del entrenamiento son como sigue:

RMSprop: algoritmo de optimización, el que hemos estado usando.
binary_crossentropy: como función objetivo debido a que en una classificación binaria la que estamos implementando.
acc (accuracy): como métrica a monitorar en el procesos de entrenamiento.

from keras import optimizers

model.compile(loss='binary_crossentropy',
              optimizer=optimizers.RMSprop(lr=1e-4),  # parámetro de paro
              #optimizer=optimizers.nadam(),
              metrics=['acc'])

Como ejercicio, es conveniente probar otros métodos de optimización como 'adagrad' [1], 'adam' [2], 'nadam'[3]

[1] John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learn-
ing and stochastic optimization. JMLR, 12:2121–2159, 2011.

[2] D. P. Kingma and J. Ba. “Adam: A Method for Stochastic Optimization.” CoRR abs/1412.6980 (2014)

[3] T. Dozat, “Incorporating Nesterov Momentum into Adam” (2016) link

Preprocesamiento de los datos

Los datos deben ser preprocesados para que puedan ser procesados en la red. El preprocesamiento consiste en

Leer la imágenes.
Ponerlas en formato de tensor: (num_imagenes, num_renglones, num_columnas, num_canales).
Mapearlas al intervalo $[0,1]$ .

Keras cuenta con herramientas de preprocesamiento para tal tarea en el paquete keras.preprocessing.image.

Usaremos la clase ImageDataGenerator para alimentar con lotes (batches) a la red y no tener que leer todas las imágenes en memoria (solo cargaremos el lote en proceso).

Primero se crean los objetos generadores.

ImageDataGenerator

from keras.preprocessing.image import ImageDataGenerator

# Rescalar los valores de los pixeles de las imágenes al intervalo [0,1]
train_datagen = ImageDataGenerator(rescale=1./255)
test_datagen  = ImageDataGenerator(rescale=1./255)

Método flow_from_directory()

Crea lotes (batch) de datos aumentados (augmented) a partir de los datos en un directorio. Se crea un lazo infinito que debe terminarse explícitamente.

Parámetros:

directory: path del directorio con los datos. Las imágenes en dicho directorio con formatos PNG, JPG, BMP, PPM or TIF se incluirán en el generador.

target_size: tamaño de todas imágenen generadas [default (256, 256)].

color_mode: {“grayscale”, “rgb”}.

classes: lista opcional de las clases indicadas como subdirectorios (e.g. [‘dogs’, ‘cats’]). Default: None.

class_mode: {“categorical”*, “binary”, “sparse”, “input” or None} Para determinar el tipo de etiquetas regresadas:

“categorical” produce un arreglo "D de códigos one-hot
“binary” produce 1D arreglo de etiquetas binarias
“input” para asociar imágenes de entrada e imágenes de salida en un sistema tipo autoencoder

batch_size: tamaño del lote (default: 32).

shuffle: remezclado de los datos (default: True).

seed: semilla aleatoria para el remezclado (shuffling)

save_to_dir: None* or filepath, para salvar los datos generados.

save_prefix: prefijo para los datos generados y salvados.

save_format: formato en que se guadan las imágenes {“png”*, “jpeg”}.

follow_links: indica si hay subdirectorios en los directorios de las clases.

Entonces creamos el generador con las siguientes características:
* lotes de 20 imágenes RGB de 150x150 (20, 150, 150, 3))
* con etiquetas binarias.

Dos generadores, uno para los datos de entrenamiento y otro para la validación.

print('Entrenamiento')
train_generator = train_datagen.flow_from_directory(
        train_dir,                # directorio con datos
        target_size=(150, 150),   # imágenes a 150x150
        batch_size=20,            # imágenes generadas por lote
        class_mode='binary')      # dado que es clasificación es binaria

print('\nValidación')
validation_generator = test_datagen.flow_from_directory(
        validation_dir,
        target_size=(150, 150),
        batch_size=20,
        class_mode='binary')

Entrenamiento
Found 2000 images belonging to 2 classes.

Validación
Found 1000 images belonging to 2 classes.

for data_batch, labels_batch in train_generator:
    print('Dimensiones del lote de datos:', data_batch.shape)
    print('Dimensiones del lote de etiquetas:', labels_batch.shape)
    break

Dimensiones del lote de datos: (20, 150, 150, 3)
Dimensiones del lote de etiquetas: (20,)

Se realiza el entrenamiento pero esta vez usando el generador para alimentar los datos de entrenamiento. Para ello usamos el método fit_generator.

fit_generator(generator, 
              steps_per_epoch    =None, 
              epochs             =1, 
              validation_data    =None, 
              validation_steps   =None, 
              class_weight       =None, 
              max_queue_size     =10, 
              shuffle            =True, 
              workers            =1, 
              use_multiprocessing=False, 
              initial_epoch      =0,
              callbacks          =None,
              verbose            =1)

Parámetros

generator, instancia de un generador Keras, la salida del generador debe ser una de:

una tupla (inputs, targets)
una tupla (inputs, targets, sample_weights).

El generador se ejecuta en paralelo con el entrenamiento y permite hacer aumento de datos en tiempo real (usar use_multiprocessing=True): aumentado de datos en CPU y entrenamiento en GPU.

steps_per_epoch: int, número total de pasos (lotes de muestras) para detener el generador

 Es importante hacer explícito detener el suministro de lotes al momento de usar los generadores.

epochs: Hace que el entrenamiento termine después del número determinado de épocas.

validation_data: Puede ser un generador o una secuencia del mismo formato que los datos

validation_steps: Si validation_data is a generator es el número total de pasos para detener el generador de datos de validación antes detenerse por el fin de cada época. Típicamente igual a número de muetras de validación dividido por el tamaño del lote.

class_weight: idem

max_queue_size: int, tamaño máximo de la cola del generador

shuffle: idem.

workers: int, máximo número de procesos (útil para generar en paralelo)

use_multiprocessing: boleano, si True, usar múltiples procesos

initial_epoch: int, época para inicar el entrenamiento, útil para continuar entrenamientos parciales

callbacks: idem

verbose: int: 0 = silencio, 1 = barra de progreso, 2 = una línea por época.

from keras import backend as K

# Resetea los pesos del modelo 
def reset_weights(model):
    session = K.get_session()
    for layer in model.layers: 
        if hasattr(layer, 'kernel_initializer'):
            layer.kernel.initializer.run(session=session)
            
reset_weights(model)

import time
tic=time.time()

history = model.fit_generator(generator        =train_generator, 
                              steps_per_epoch  =100, 
                              epochs           =30, 
                              validation_data  =validation_generator, 
                              validation_steps =50,
                              verbose          =2,
                              max_queue_size   =12,
                              workers          =12)
                              #use_multiprocessing=True)

print('seconds=', time.time()-tic)

Epoch 1/30
 - 2s - loss: 0.6887 - acc: 0.5350 - val_loss: 0.6769 - val_acc: 0.5450
Epoch 2/30
 - 2s - loss: 0.6715 - acc: 0.5835 - val_loss: 0.6502 - val_acc: 0.6250
Epoch 3/30
 - 2s - loss: 0.6495 - acc: 0.6105 - val_loss: 0.6323 - val_acc: 0.6460
Epoch 4/30
 - 2s - loss: 0.6338 - acc: 0.6360 - val_loss: 0.6201 - val_acc: 0.6630
Epoch 5/30
 - 2s - loss: 0.6188 - acc: 0.6510 - val_loss: 0.6291 - val_acc: 0.6520
Epoch 6/30
 - 2s - loss: 0.5995 - acc: 0.6740 - val_loss: 0.6081 - val_acc: 0.6730
Epoch 7/30
 - 2s - loss: 0.5813 - acc: 0.7010 - val_loss: 0.5968 - val_acc: 0.6690
Epoch 8/30
 - 2s - loss: 0.5528 - acc: 0.7245 - val_loss: 0.5808 - val_acc: 0.6830
Epoch 9/30
 - 2s - loss: 0.5277 - acc: 0.7390 - val_loss: 0.6307 - val_acc: 0.6590
Epoch 10/30
 - 2s - loss: 0.5108 - acc: 0.7510 - val_loss: 0.5665 - val_acc: 0.7010
Epoch 11/30
 - 2s - loss: 0.4819 - acc: 0.7730 - val_loss: 0.5725 - val_acc: 0.7040
Epoch 12/30
 - 2s - loss: 0.4546 - acc: 0.7880 - val_loss: 0.5591 - val_acc: 0.7030
Epoch 13/30
 - 2s - loss: 0.4406 - acc: 0.7875 - val_loss: 0.5643 - val_acc: 0.6980
Epoch 14/30
 - 2s - loss: 0.4156 - acc: 0.8135 - val_loss: 0.6520 - val_acc: 0.6900
Epoch 15/30
 - 2s - loss: 0.3960 - acc: 0.8210 - val_loss: 0.5602 - val_acc: 0.7180
Epoch 16/30
 - 2s - loss: 0.3693 - acc: 0.8430 - val_loss: 0.6387 - val_acc: 0.6910
Epoch 17/30
 - 2s - loss: 0.3449 - acc: 0.8560 - val_loss: 0.5817 - val_acc: 0.7280
Epoch 18/30
 - 2s - loss: 0.3220 - acc: 0.8610 - val_loss: 0.5633 - val_acc: 0.7360
Epoch 19/30
 - 2s - loss: 0.2976 - acc: 0.8825 - val_loss: 0.5803 - val_acc: 0.7190
Epoch 20/30
 - 2s - loss: 0.2759 - acc: 0.8935 - val_loss: 0.5855 - val_acc: 0.7410
Epoch 21/30
 - 2s - loss: 0.2462 - acc: 0.9090 - val_loss: 0.6168 - val_acc: 0.7250
Epoch 22/30
 - 2s - loss: 0.2243 - acc: 0.9140 - val_loss: 0.6110 - val_acc: 0.7290
Epoch 23/30
 - 2s - loss: 0.2005 - acc: 0.9235 - val_loss: 0.6377 - val_acc: 0.7160
Epoch 24/30
 - 2s - loss: 0.1924 - acc: 0.9275 - val_loss: 0.6665 - val_acc: 0.7170
Epoch 25/30
 - 2s - loss: 0.1588 - acc: 0.9410 - val_loss: 0.6939 - val_acc: 0.7250
Epoch 26/30
 - 2s - loss: 0.1440 - acc: 0.9505 - val_loss: 0.7069 - val_acc: 0.7310
Epoch 27/30
 - 2s - loss: 0.1317 - acc: 0.9555 - val_loss: 0.7591 - val_acc: 0.7270
Epoch 28/30
 - 2s - loss: 0.1143 - acc: 0.9595 - val_loss: 0.7407 - val_acc: 0.7270
Epoch 29/30
 - 2s - loss: 0.0988 - acc: 0.9690 - val_loss: 0.8235 - val_acc: 0.7160
Epoch 30/30
 - 2s - loss: 0.0840 - acc: 0.9720 - val_loss: 0.9263 - val_acc: 0.7100
seconds= 52.77987456321716

workerstime={1 :234.4, 
             2 :123.83, 
             3 : 88.74,
             4 : 72.27, 
             5 : 64.73,
             6 : 60.82,
             7 : 58.11,
             8 : 55.42,
             9 : 53.47,
             10: 52.93,
             11: 53.42,
             12: 52.77}

workers=workerstime.keys()
wtime=[workerstime[w] for w in workers]

import matplotlib.pyplot as plt
plt.plot(workers, wtime, 'o')
plt.title('Tiempo vs Threads')
plt.ylabel('secs')
plt.xlabel('Num. hilos')
plt.show()

png

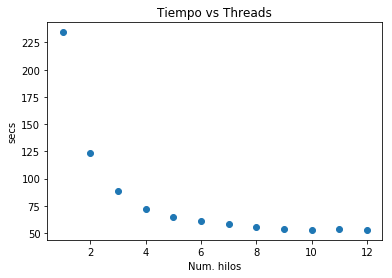
Sin multitarea: 4.1 min (242s)

Con multitarea: 0.9min (55s)
* workers =8,

Luego salvamos el modelo

model.save('cats_and_dogs_small_2.h5')

Y analizamos las gráficas del proceso de entrenamiento (training)

%matplotlib inline

import matplotlib.pyplot as plt

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(len(acc))

plt.figure(figsize=(8,10))

plt.subplot(211)
plt.plot(epochs, acc, 'bo', label='Entrenamiento acc')
plt.plot(epochs, val_acc, 'b', label='Validacion acc')
plt.title('Exactitud (accuracy) de entrenamiento y validacion')
plt.legend()

plt.subplot(212)
plt.plot(epochs, loss, 'bo', label='Entrenamiento costo')
plt.plot(epochs, val_loss, 'b', label='Validacion cost')
plt.title('Costo (loss) de entrenamiento y validacion')
plt.legend()

plt.show()

png

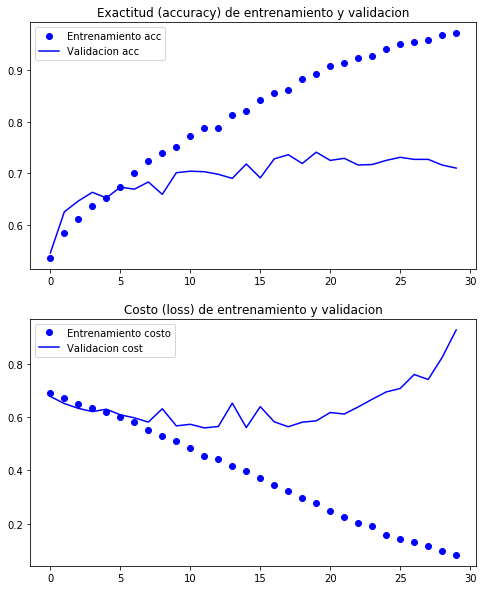
Note que la medida de exactitud (accuracy) sobre los datos de entrenamiento se incrementa conforme pasan las épocas llegando prácticamente al $100 \%$ . Sin embargo, dicha medida se estanca mucho antes para los datos de validación, quedando cerca del $75 \%$ . Esto es típico de un sobreajuste (over-fitting): las pocas muestras de entrenamiento son memorizadas y no se consigue un buen poder de generalización para datos no observados. Por ello, es necesario hacer aumento de datos (data augmentation).

Aumento de Datos

Para reducir el problema de sobreajuste por usar un conjunto de entrenamiento relativamente pequeño que no permita tener un buen muestreo del espacio de los datos usaremos aumento de datos. Esta técnica consiste en aplicar transfomaciones a los datos (imágenes) de entrenamiento que generen nuevos datos con una apariencia realista. Con ello ampliamos las muestra.

Un ejemplo de aumento de datos, es aplicar a las imágenes una reflección sobre el eje vertical, tal como se verían las imágenes reflejadas en un espejo. Dado que estamos lidiando con imágenes que de perros y gatos, parece una forma natural de aumentar la muestra.

Para el caso de imágenes, el aumento de datos es posible codificarlo a través del generador de datos ImageDataGenerator. Para lo cual revisamos la definición y sus parámetros por default:

keras.preprocessing.image.ImageDataGenerator(featurewise_center=False, 
                                             samplewise_center=False, 
                                             featurewise_std_normalization=False, 
                                             samplewise_std_normalization=False, 
                                             zca_whitening=False, 
                                             zca_epsilon=1e-06, 
                                             rotation_range=0, 
                                             width_shift_range=0.0, 
                                             height_shift_range=0.0, 
                                             brightness_range=None, 
                                             shear_range=0.0, 
                                             zoom_range=0.0, 
                                             channel_shift_range=0.0, 
                                             fill_mode='nearest', 
                                             cval=0.0, 
                                             horizontal_flip=False, 
                                             vertical_flip=False, 
                                             rescale=None, 
                                             preprocessing_function=None, 
                                             data_format=None, 
                                             validation_split=0.0, 
                                             dtype=None)```
             

Parámetros

**featurewise_center**: *Boleana*, poner la media de cada elemento (**feature-wise**) en cero de todos los datos.

**samplewise_center**: Boleana, poener la media del cada muestra a cero

**featurewise_std_normalization**: Boleana, dividir cada elemento por la desviación estándar (std.)

**samplewise_std_normalization**: Boleana, dividir cada dato por su std.

**zca_epsilon**: épsilon para blanqueo ZCA.

**zca_whitening**: Boleana, indica si se aplica el blanqueo ZCA. Esto es

Componentes Principales

Sigma = x.T @ x) / x.shape[0]
U, S, V = linalg.svd(Sigma)
D = np.diag(1./np.sqrt(S + epsilon))
PrinComp = U @ D @ U.T

blanqueo ZCA

tilde_x = x @ PrinComp


**rotation_range**: `int`, Rango en grados para aplicar rotaciones aleatorias

**width_shift_range**: Desplazamientos aleatorios por columna 

Si es un escalar, se aplica por renglones
   
   * `float`: $[0,1)$, fracción de la dimensión total del rango del corrimiento aleatorio
   
   * `int`$\ge 1$, rango en pixeles del despazamiento

Si es arreglo 1D, son los elementos para elegir los corrimientos.

**height_shift_range**: desplazamientos aleatorios por renglón.


**brightness_range**: Tupla de dos `float`, rango para seleccionar los corrimientos en brillantez de los canales de las imágenes

**shear_range**: `float`. rango del cizallamiento 

**zoom_range**: `float` o $[lower, upper]$. Rango para los el zoom aleatorio


**channel_shift_range**: `float`, rango para corrimiento por canales

**fill_mode**: Modo de interpolación, opciones son \{"constant", "nearest", "reflect" or "wrap"\}. Los puntos fuera de las fronteras se rellenas de acuerod con las siguientes reglas:

   * 'constant': kkkkkkkk|abcd|kkkkkkkk (cval=k)

   * 'nearest': aaaaaaaa|abcd|dddddddd

   * 'reflect': abcddcba|abcd|dcbaabcd
   
   * 'wrap': abcdabcd|abcd|abcdabcd
   
   donde cval: `float`  or `int` es el valor usado para rellenar

**horizontal_flip**: Boleana, reflejar aleatoriamente las entradas horizontalmente

**vertical_flip**: Boleana, reflejar aleatoriamente las entradas verticalmente

**rescale**: factor de rescalamiento aplicados despues de todas las transformaciones aleatorias.

**preprocessing_function**: función aplicada a todas las entradas. La función debe recibir como entrada un arreglo `numpy` con la imagen RGB (tensor de rango 3) y devuelve una arreglo con las mismas dimensiones.

**data_format**. {"channels_first", "channels_last"}

**validation_split**: `float`, fracción de imágenes reservadas para validación

**dtype**: `dtype` de los arreglos generados

Usaremos



```python
datagen = ImageDataGenerator(
      rotation_range    =40,
      width_shift_range =0.2,
      height_shift_range=0.2,
      shear_range       =0.2,
      zoom_range        =0.2,
      horizontal_flip   =True,
      fill_mode         ='nearest')

Ejemplo de como se ven los datos aumentados

# Modulo de proprocesamiento de imágenes en Keras 
from keras.preprocessing import image

# lista con los nombres de los archivos para entrenamiento 
fnames = [os.path.join(train_cats_dir, fname) for fname in os.listdir(train_cats_dir)]

# Selección de una imagen
img_path = fnames[10]

# lectura y ajuste de la dimensión a la de trabajo
img = image.load_img(img_path, target_size=(150, 150))

# conversión a arreglo numpy 3D, forma (150, 150, 3)
x = image.img_to_array(img)
x = x.reshape((1,) + x.shape)

plt.figure(figsize=(10,10))

# data.flow() genera datos indefinidamente, lo detenemos 
# justo después de generar 4 datos aumentados
i = 0
for batch in datagen.flow(x, batch_size=1):
    plt.subplot(2,2, i+1)
    plt.imshow(image.array_to_img(batch[0]))
    plt.axis('off')
    i += 1
    if i % 4 == 0:
        break

plt.show()

png

Usar el generador aleatorio permite alimentar a la red con datos frescos que nunca has sido vistos (exectamente).

Sin embargo, como podemos observar en las imágenes generadas, los datos estan altamente correlacionados. Por ello, se agrega una capa Dropout antes del la etapa de clasificación.

Keras.layers.Dropout(rate, noise_shape=None, seed=None)

Para prevenir overfitting, aleatoriamente elimina datos (dropout) de entrada.

Parámetros

rate: float [0,1] fracción de datos de entrada que son desechadas

noise_shape: forma de la máscara aleatoria que se usa como multiplicador de la entrada para implementar el dropout. Si, por ejemplo, la entrada tienen dimensiones=(batch_size, timesteps, features), y se desea que la máscara sea la misma para todos los timesteps, usamos noise_shape=(batch_size, 1, features); usa broadcasting de python.

seed: int, semilla para generar la máscara

La siguiente figura, tomada de _[4], ilustra el proceso de dropout. El panel de la izquierda muestra los pesos normales, y el de la derecha el dropout de unidades al enmascarar su salida . El enmascarado de unidades, es solo aplicado para un lote, al siguiente lote se aplica una nueva máscara aleatoria.

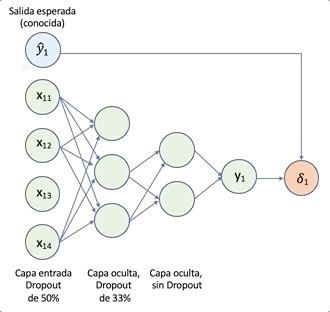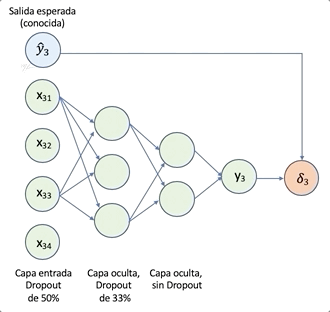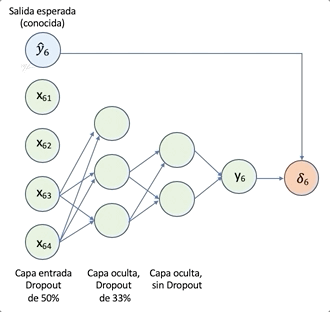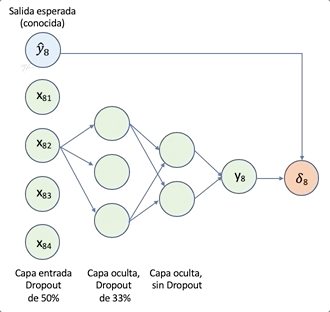
dropout

Referencia

[4] N. Srivastav et al., Dropout: A Simple Way to Prevent Neural Networks from Overfitting, JMLR, (15) 6-14, 2014] (http://www.jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf)

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
                        input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dropout(0.5))
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(loss='binary_crossentropy',
              #optimizer=optimizers.RMSprop(lr=1e-4),
              optimizer=optimizers.nadam(),
              metrics=['acc'])

Entrenemos la red ahora con Aumentación de Datos y Descarte (Dopout)

train_datagen = ImageDataGenerator(rescale            =1./255,
                                   rotation_range     =40,
                                   width_shift_range  =0.2,
                                   height_shift_range =0.2,
                                   shear_range        =0.2,
                                   zoom_range         =0.2,
                                   horizontal_flip    =True,)

# Los datos de validación no se aumentan!
test_datagen = ImageDataGenerator(rescale=1./255)

train_generator = train_datagen.flow_from_directory(
        train_dir,                # Directorio con los datos
        target_size=(150, 150),   # imagenes ajustadas a 150x150 pixeles
        batch_size=32,            # tamaño del lote 
        class_mode='binary')      # problema de clasifició binario 

validation_generator = test_datagen.flow_from_directory(
        validation_dir,
        target_size=(150, 150),
        batch_size=32,
        class_mode='binary')

# Probando los generadores
for data_batch, labels_batch in train_generator:
    print('Dimensiones (shape) de los datos:', data_batch.shape)
    print('Dimensiones (shape) de las etiquetas:', labels_batch.shape)
    break

Found 2000 images belonging to 2 classes.
Found 1000 images belonging to 2 classes.
Dimensiones (shape) de los datos: (32, 150, 150, 3)
Dimensiones (shape) de las etiquetas: (32,)

reset_weights(model)

import time
tstart = time.time()

history = model.fit_generator(generator       =train_generator,
                              steps_per_epoch =100,
                              epochs          =200,
                              validation_data =validation_generator,
                              validation_steps=50,
                              workers         =12,
                              initial_epoch   =0,
                              use_multiprocessing=False,
                              verbose         =2)

print('seconds=', time.time()-tstart)

Epoch 1/200
 - 5s - loss: 0.2212 - acc: 0.9059 - val_loss: 0.4544 - val_acc: 0.8582
Epoch 2/200
 - 4s - loss: 0.2133 - acc: 0.9131 - val_loss: 0.5215 - val_acc: 0.8293
Epoch 3/200
 - 4s - loss: 0.2117 - acc: 0.9147 - val_loss: 0.4707 - val_acc: 0.8512
Epoch 4/200
 - 4s - loss: 0.2197 - acc: 0.9097 - val_loss: 0.4619 - val_acc: 0.8553
Epoch 5/200
 - 4s - loss: 0.2300 - acc: 0.9078 - val_loss: 0.4347 - val_acc: 0.8557
Epoch 6/200
 - 4s - loss: 0.2284 - acc: 0.9009 - val_loss: 0.3963 - val_acc: 0.8660
Epoch 7/200
 - 4s - loss: 0.2064 - acc: 0.9131 - val_loss: 0.4269 - val_acc: 0.8629
Epoch 8/200
 - 4s - loss: 0.2375 - acc: 0.9006 - val_loss: 0.4400 - val_acc: 0.8512
Epoch 9/200
 - 4s - loss: 0.2199 - acc: 0.9034 - val_loss: 0.5601 - val_acc: 0.8490
Epoch 10/200
 - 4s - loss: 0.2418 - acc: 0.8944 - val_loss: 0.4011 - val_acc: 0.8550
Epoch 11/200
 - 5s - loss: 0.1873 - acc: 0.9172 - val_loss: 0.4757 - val_acc: 0.8534
Epoch 12/200
 - 4s - loss: 0.2044 - acc: 0.9153 - val_loss: 0.5029 - val_acc: 0.8647
Epoch 13/200
 - 4s - loss: 0.2157 - acc: 0.9141 - val_loss: 0.5484 - val_acc: 0.8396
Epoch 14/200
 - 4s - loss: 0.2088 - acc: 0.9072 - val_loss: 0.5089 - val_acc: 0.8541
Epoch 15/200
 - 4s - loss: 0.2058 - acc: 0.9184 - val_loss: 0.4912 - val_acc: 0.8653
Epoch 16/200
 - 4s - loss: 0.2144 - acc: 0.9084 - val_loss: 0.4553 - val_acc: 0.8579
Epoch 17/200
 - 4s - loss: 0.2048 - acc: 0.9209 - val_loss: 0.4764 - val_acc: 0.8705
Epoch 18/200
 - 4s - loss: 0.2285 - acc: 0.9025 - val_loss: 0.5044 - val_acc: 0.8687
Epoch 19/200
 - 4s - loss: 0.2242 - acc: 0.9066 - val_loss: 0.4945 - val_acc: 0.8479
Epoch 20/200
 - 4s - loss: 0.2301 - acc: 0.9088 - val_loss: 0.4148 - val_acc: 0.8826
Epoch 21/200
 - 4s - loss: 0.2077 - acc: 0.9159 - val_loss: 0.4525 - val_acc: 0.8705
Epoch 22/200
 - 4s - loss: 0.1953 - acc: 0.9219 - val_loss: 0.4680 - val_acc: 0.8814
Epoch 23/200
 - 4s - loss: 0.2217 - acc: 0.9119 - val_loss: 0.4811 - val_acc: 0.8382
Epoch 24/200
 - 4s - loss: 0.2254 - acc: 0.8994 - val_loss: 0.4340 - val_acc: 0.8653
Epoch 25/200
 - 4s - loss: 0.2240 - acc: 0.9131 - val_loss: 0.4265 - val_acc: 0.8706
Epoch 26/200
 - 4s - loss: 0.2016 - acc: 0.9172 - val_loss: 0.4165 - val_acc: 0.8756
Epoch 27/200
 - 4s - loss: 0.2085 - acc: 0.9156 - val_loss: 0.5494 - val_acc: 0.8363
Epoch 28/200
 - 4s - loss: 0.2263 - acc: 0.9081 - val_loss: 0.3930 - val_acc: 0.8782
Epoch 29/200
 - 4s - loss: 0.1928 - acc: 0.9109 - val_loss: 0.4890 - val_acc: 0.8634
Epoch 30/200
 - 4s - loss: 0.2079 - acc: 0.9147 - val_loss: 0.4595 - val_acc: 0.8674
Epoch 31/200
 - 4s - loss: 0.1996 - acc: 0.9184 - val_loss: 0.4740 - val_acc: 0.8531
Epoch 32/200
 - 4s - loss: 0.2179 - acc: 0.9072 - val_loss: 0.5789 - val_acc: 0.8464
Epoch 33/200
 - 4s - loss: 0.2207 - acc: 0.9034 - val_loss: 0.3998 - val_acc: 0.8731
Epoch 34/200
 - 4s - loss: 0.2161 - acc: 0.9094 - val_loss: 0.4642 - val_acc: 0.8458
Epoch 35/200
 - 4s - loss: 0.2158 - acc: 0.9119 - val_loss: 0.4198 - val_acc: 0.8570
Epoch 36/200
 - 4s - loss: 0.2041 - acc: 0.9181 - val_loss: 0.3977 - val_acc: 0.8718
Epoch 37/200
 - 4s - loss: 0.2142 - acc: 0.9137 - val_loss: 0.4629 - val_acc: 0.8634
Epoch 38/200
 - 4s - loss: 0.2170 - acc: 0.9106 - val_loss: 0.3562 - val_acc: 0.8789
Epoch 39/200
 - 4s - loss: 0.2022 - acc: 0.9209 - val_loss: 0.4375 - val_acc: 0.8699
Epoch 40/200
 - 4s - loss: 0.2198 - acc: 0.9147 - val_loss: 0.4148 - val_acc: 0.8615
Epoch 41/200
 - 4s - loss: 0.2274 - acc: 0.9034 - val_loss: 0.4239 - val_acc: 0.8642
Epoch 42/200
 - 4s - loss: 0.2052 - acc: 0.9147 - val_loss: 0.4865 - val_acc: 0.8615
Epoch 43/200
 - 4s - loss: 0.1989 - acc: 0.9250 - val_loss: 0.4553 - val_acc: 0.8642
Epoch 44/200
 - 4s - loss: 0.2185 - acc: 0.9088 - val_loss: 0.4577 - val_acc: 0.8621
Epoch 45/200
 - 4s - loss: 0.1934 - acc: 0.9200 - val_loss: 0.4699 - val_acc: 0.8550
Epoch 46/200
 - 4s - loss: 0.1998 - acc: 0.9172 - val_loss: 0.4868 - val_acc: 0.8553
Epoch 47/200
 - 4s - loss: 0.2202 - acc: 0.9106 - val_loss: 0.3762 - val_acc: 0.8698
Epoch 48/200
 - 4s - loss: 0.2255 - acc: 0.9147 - val_loss: 0.4908 - val_acc: 0.8274
Epoch 49/200
 - 4s - loss: 0.2076 - acc: 0.9103 - val_loss: 0.4677 - val_acc: 0.8576
Epoch 50/200
 - 4s - loss: 0.2159 - acc: 0.9094 - val_loss: 0.4169 - val_acc: 0.8610
Epoch 51/200
 - 4s - loss: 0.2068 - acc: 0.9159 - val_loss: 0.4125 - val_acc: 0.8660
Epoch 52/200
 - 4s - loss: 0.2049 - acc: 0.9194 - val_loss: 0.5108 - val_acc: 0.8566
Epoch 53/200
 - 4s - loss: 0.2051 - acc: 0.9116 - val_loss: 0.4089 - val_acc: 0.8589
Epoch 54/200
 - 4s - loss: 0.2029 - acc: 0.9178 - val_loss: 0.5031 - val_acc: 0.8518
Epoch 55/200
 - 4s - loss: 0.2139 - acc: 0.9169 - val_loss: 0.4390 - val_acc: 0.8718
Epoch 56/200
 - 4s - loss: 0.2343 - acc: 0.9041 - val_loss: 0.4616 - val_acc: 0.8499
Epoch 57/200
 - 4s - loss: 0.1994 - acc: 0.9184 - val_loss: 0.6079 - val_acc: 0.8331
Epoch 58/200
 - 4s - loss: 0.2009 - acc: 0.9200 - val_loss: 0.4526 - val_acc: 0.8827
Epoch 59/200
 - 4s - loss: 0.2000 - acc: 0.9219 - val_loss: 0.5499 - val_acc: 0.8598
Epoch 60/200
 - 4s - loss: 0.1899 - acc: 0.9184 - val_loss: 0.4405 - val_acc: 0.8692
Epoch 61/200
 - 5s - loss: 0.1926 - acc: 0.9181 - val_loss: 0.4203 - val_acc: 0.8763
Epoch 62/200
 - 5s - loss: 0.2128 - acc: 0.9119 - val_loss: 0.4637 - val_acc: 0.8471
Epoch 63/200
 - 4s - loss: 0.2054 - acc: 0.9237 - val_loss: 0.5584 - val_acc: 0.8512
Epoch 64/200
 - 5s - loss: 0.1945 - acc: 0.9122 - val_loss: 0.4962 - val_acc: 0.8490
Epoch 65/200
 - 4s - loss: 0.2105 - acc: 0.9112 - val_loss: 0.3839 - val_acc: 0.8705
Epoch 66/200
 - 5s - loss: 0.2533 - acc: 0.9100 - val_loss: 0.4670 - val_acc: 0.8725
Epoch 67/200
 - 4s - loss: 0.2872 - acc: 0.8816 - val_loss: 0.3682 - val_acc: 0.8447
Epoch 68/200
 - 4s - loss: 0.2371 - acc: 0.9072 - val_loss: 0.4033 - val_acc: 0.8617
Epoch 69/200
 - 4s - loss: 0.2076 - acc: 0.9075 - val_loss: 0.4450 - val_acc: 0.8576
Epoch 70/200
 - 5s - loss: 0.2106 - acc: 0.9178 - val_loss: 0.3826 - val_acc: 0.8698
Epoch 71/200
 - 4s - loss: 0.2017 - acc: 0.9162 - val_loss: 0.4435 - val_acc: 0.8572
Epoch 72/200
 - 4s - loss: 0.2042 - acc: 0.9188 - val_loss: 0.4611 - val_acc: 0.8621
Epoch 73/200
 - 5s - loss: 0.2089 - acc: 0.9069 - val_loss: 0.4497 - val_acc: 0.8794
Epoch 74/200
 - 5s - loss: 0.2011 - acc: 0.9131 - val_loss: 0.5358 - val_acc: 0.8344
Epoch 75/200
 - 4s - loss: 0.1979 - acc: 0.9194 - val_loss: 0.4155 - val_acc: 0.8591
Epoch 76/200
 - 4s - loss: 0.1836 - acc: 0.9281 - val_loss: 0.3741 - val_acc: 0.8808
Epoch 77/200
 - 5s - loss: 0.1889 - acc: 0.9256 - val_loss: 0.4066 - val_acc: 0.8698
Epoch 78/200
 - 4s - loss: 0.2124 - acc: 0.9141 - val_loss: 0.3826 - val_acc: 0.8553
Epoch 79/200
 - 4s - loss: 0.2098 - acc: 0.9128 - val_loss: 0.4481 - val_acc: 0.8409
Epoch 80/200
 - 4s - loss: 0.2081 - acc: 0.9094 - val_loss: 0.5257 - val_acc: 0.8503
Epoch 81/200
 - 4s - loss: 0.1953 - acc: 0.9194 - val_loss: 0.3638 - val_acc: 0.8853
Epoch 82/200
 - 4s - loss: 0.2086 - acc: 0.9178 - val_loss: 0.3702 - val_acc: 0.8687
Epoch 83/200
 - 4s - loss: 0.1896 - acc: 0.9191 - val_loss: 0.4220 - val_acc: 0.8724
Epoch 84/200
 - 5s - loss: 0.1870 - acc: 0.9228 - val_loss: 0.3802 - val_acc: 0.8718
Epoch 85/200
 - 4s - loss: 0.1887 - acc: 0.9216 - val_loss: 0.5069 - val_acc: 0.8563
Epoch 86/200
 - 5s - loss: 0.2067 - acc: 0.9203 - val_loss: 0.4759 - val_acc: 0.8518
Epoch 87/200
 - 5s - loss: 0.2029 - acc: 0.9131 - val_loss: 0.4643 - val_acc: 0.8648
Epoch 88/200
 - 5s - loss: 0.1892 - acc: 0.9228 - val_loss: 0.4710 - val_acc: 0.8653
Epoch 89/200
 - 4s - loss: 0.1941 - acc: 0.9256 - val_loss: 0.5255 - val_acc: 0.8604
Epoch 90/200
 - 4s - loss: 0.1851 - acc: 0.9219 - val_loss: 0.4426 - val_acc: 0.8711
Epoch 91/200
 - 4s - loss: 0.2031 - acc: 0.9150 - val_loss: 0.5472 - val_acc: 0.8496
Epoch 92/200
 - 4s - loss: 0.1968 - acc: 0.9238 - val_loss: 0.4228 - val_acc: 0.8853
Epoch 93/200
 - 4s - loss: 0.1974 - acc: 0.9194 - val_loss: 0.4606 - val_acc: 0.8550
Epoch 94/200
 - 5s - loss: 0.1949 - acc: 0.9209 - val_loss: 0.4443 - val_acc: 0.8452
Epoch 95/200
 - 5s - loss: 0.1899 - acc: 0.9169 - val_loss: 0.4556 - val_acc: 0.8666
Epoch 96/200
 - 4s - loss: 0.2061 - acc: 0.9141 - val_loss: 0.4276 - val_acc: 0.8560
Epoch 97/200
 - 5s - loss: 0.1851 - acc: 0.9278 - val_loss: 0.4011 - val_acc: 0.8789
Epoch 98/200
 - 5s - loss: 0.2069 - acc: 0.9206 - val_loss: 0.4996 - val_acc: 0.8610
Epoch 99/200
 - 5s - loss: 0.2148 - acc: 0.9122 - val_loss: 0.4751 - val_acc: 0.8711
Epoch 100/200
 - 4s - loss: 0.2192 - acc: 0.9103 - val_loss: 0.4718 - val_acc: 0.8623
Epoch 101/200
 - 4s - loss: 0.1886 - acc: 0.9212 - val_loss: 0.4860 - val_acc: 0.8814
Epoch 102/200
 - 4s - loss: 0.2103 - acc: 0.9222 - val_loss: 0.4387 - val_acc: 0.8621
Epoch 103/200
 - 4s - loss: 0.1757 - acc: 0.9262 - val_loss: 0.4338 - val_acc: 0.8801
Epoch 104/200
 - 4s - loss: 0.2043 - acc: 0.9156 - val_loss: 0.4395 - val_acc: 0.8621
Epoch 105/200
 - 4s - loss: 0.2002 - acc: 0.9128 - val_loss: 0.5218 - val_acc: 0.8490
Epoch 106/200
 - 4s - loss: 0.1879 - acc: 0.9250 - val_loss: 0.4714 - val_acc: 0.8711
Epoch 107/200
 - 4s - loss: 0.1984 - acc: 0.9166 - val_loss: 0.4905 - val_acc: 0.8636
Epoch 108/200
 - 4s - loss: 0.1835 - acc: 0.9219 - val_loss: 0.6235 - val_acc: 0.8544
Epoch 109/200
 - 4s - loss: 0.1928 - acc: 0.9244 - val_loss: 0.4454 - val_acc: 0.8776
Epoch 110/200
 - 4s - loss: 0.1808 - acc: 0.9288 - val_loss: 0.4628 - val_acc: 0.8610
Epoch 111/200
 - 4s - loss: 0.2031 - acc: 0.9200 - val_loss: 0.4163 - val_acc: 0.8563
Epoch 112/200
 - 4s - loss: 0.1939 - acc: 0.9194 - val_loss: 0.3248 - val_acc: 0.8845
Epoch 113/200
 - 4s - loss: 0.2010 - acc: 0.9175 - val_loss: 0.5133 - val_acc: 0.8499
Epoch 114/200
 - 4s - loss: 0.1988 - acc: 0.9200 - val_loss: 0.4423 - val_acc: 0.8706
Epoch 115/200
 - 4s - loss: 0.2264 - acc: 0.9091 - val_loss: 0.4219 - val_acc: 0.8634
Epoch 116/200
 - 4s - loss: 0.2112 - acc: 0.9169 - val_loss: 0.4592 - val_acc: 0.8750
Epoch 117/200
 - 4s - loss: 0.1928 - acc: 0.9172 - val_loss: 0.4103 - val_acc: 0.8724
Epoch 118/200
 - 4s - loss: 0.1898 - acc: 0.9197 - val_loss: 0.4310 - val_acc: 0.8724
Epoch 119/200
 - 4s - loss: 0.1960 - acc: 0.9194 - val_loss: 0.4245 - val_acc: 0.8718
Epoch 120/200
 - 4s - loss: 0.1886 - acc: 0.9250 - val_loss: 0.4097 - val_acc: 0.8711
Epoch 121/200
 - 4s - loss: 0.1797 - acc: 0.9288 - val_loss: 0.4324 - val_acc: 0.8598
Epoch 122/200
 - 4s - loss: 0.1950 - acc: 0.9250 - val_loss: 0.5619 - val_acc: 0.8557
Epoch 123/200
 - 4s - loss: 0.1914 - acc: 0.9200 - val_loss: 0.5164 - val_acc: 0.8661
Epoch 124/200
 - 4s - loss: 0.2137 - acc: 0.9134 - val_loss: 0.3739 - val_acc: 0.8750
Epoch 125/200
 - 4s - loss: 0.2068 - acc: 0.9266 - val_loss: 0.3973 - val_acc: 0.8673
Epoch 126/200
 - 4s - loss: 0.1816 - acc: 0.9247 - val_loss: 0.4911 - val_acc: 0.8572
Epoch 127/200
 - 4s - loss: 0.1981 - acc: 0.9222 - val_loss: 0.4374 - val_acc: 0.8673
Epoch 128/200
 - 4s - loss: 0.2116 - acc: 0.9181 - val_loss: 0.4404 - val_acc: 0.8572
Epoch 129/200
 - 4s - loss: 0.1978 - acc: 0.9159 - val_loss: 0.4108 - val_acc: 0.8686
Epoch 130/200
 - 4s - loss: 0.1806 - acc: 0.9253 - val_loss: 0.3852 - val_acc: 0.8769
Epoch 131/200
 - 4s - loss: 0.1908 - acc: 0.9209 - val_loss: 0.5249 - val_acc: 0.8557
Epoch 132/200
 - 4s - loss: 0.2172 - acc: 0.9144 - val_loss: 0.4280 - val_acc: 0.8687
Epoch 133/200
 - 4s - loss: 0.1806 - acc: 0.9247 - val_loss: 0.4266 - val_acc: 0.8698
Epoch 134/200
 - 4s - loss: 0.1780 - acc: 0.9278 - val_loss: 0.4877 - val_acc: 0.8724
Epoch 135/200
 - 4s - loss: 0.1979 - acc: 0.9181 - val_loss: 0.5762 - val_acc: 0.8230
Epoch 136/200
 - 4s - loss: 0.2118 - acc: 0.9141 - val_loss: 0.3661 - val_acc: 0.8698
Epoch 137/200
 - 4s - loss: 0.1818 - acc: 0.9234 - val_loss: 0.4288 - val_acc: 0.8731
Epoch 138/200
 - 4s - loss: 0.2038 - acc: 0.9178 - val_loss: 0.4111 - val_acc: 0.8711
Epoch 139/200
 - 4s - loss: 0.1796 - acc: 0.9322 - val_loss: 0.4711 - val_acc: 0.8801
Epoch 140/200
 - 4s - loss: 0.1890 - acc: 0.9231 - val_loss: 0.4414 - val_acc: 0.8692
Epoch 141/200
 - 4s - loss: 0.2080 - acc: 0.9191 - val_loss: 0.4780 - val_acc: 0.8621
Epoch 142/200
 - 4s - loss: 0.1833 - acc: 0.9297 - val_loss: 0.5086 - val_acc: 0.8515
Epoch 143/200
 - 4s - loss: 0.2021 - acc: 0.9156 - val_loss: 0.4869 - val_acc: 0.8686
Epoch 144/200
 - 4s - loss: 0.1698 - acc: 0.9322 - val_loss: 0.4730 - val_acc: 0.8477
Epoch 145/200
 - 4s - loss: 0.2020 - acc: 0.9209 - val_loss: 0.4893 - val_acc: 0.8563
Epoch 146/200
 - 4s - loss: 0.1975 - acc: 0.9184 - val_loss: 0.4749 - val_acc: 0.8680
Epoch 147/200
 - 4s - loss: 0.1806 - acc: 0.9241 - val_loss: 0.4282 - val_acc: 0.8705
Epoch 148/200
 - 4s - loss: 0.1945 - acc: 0.9244 - val_loss: 0.4121 - val_acc: 0.8712
Epoch 149/200
 - 4s - loss: 0.1793 - acc: 0.9281 - val_loss: 0.4591 - val_acc: 0.8718
Epoch 150/200
 - 4s - loss: 0.1970 - acc: 0.9203 - val_loss: 0.3958 - val_acc: 0.8750
Epoch 151/200
 - 4s - loss: 0.1736 - acc: 0.9325 - val_loss: 0.4401 - val_acc: 0.8731
Epoch 152/200
 - 4s - loss: 0.2001 - acc: 0.9203 - val_loss: 0.3878 - val_acc: 0.8827
Epoch 153/200
 - 4s - loss: 0.1818 - acc: 0.9275 - val_loss: 0.4898 - val_acc: 0.8553
Epoch 154/200
 - 4s - loss: 0.1840 - acc: 0.9284 - val_loss: 0.4795 - val_acc: 0.8795
Epoch 155/200
 - 4s - loss: 0.1757 - acc: 0.9303 - val_loss: 0.4509 - val_acc: 0.8744
Epoch 156/200
 - 4s - loss: 0.1805 - acc: 0.9325 - val_loss: 0.5511 - val_acc: 0.8718
Epoch 157/200
 - 4s - loss: 0.1994 - acc: 0.9153 - val_loss: 0.6478 - val_acc: 0.8512
Epoch 158/200
 - 4s - loss: 0.1882 - acc: 0.9216 - val_loss: 0.4450 - val_acc: 0.8642
Epoch 159/200
 - 4s - loss: 0.1886 - acc: 0.9222 - val_loss: 0.4963 - val_acc: 0.8640
Epoch 160/200
 - 4s - loss: 0.1721 - acc: 0.9287 - val_loss: 0.4253 - val_acc: 0.8801
Epoch 161/200
 - 4s - loss: 0.1775 - acc: 0.9347 - val_loss: 0.5596 - val_acc: 0.8499
Epoch 162/200
 - 4s - loss: 0.1784 - acc: 0.9287 - val_loss: 0.4342 - val_acc: 0.8731
Epoch 163/200
 - 4s - loss: 0.1611 - acc: 0.9356 - val_loss: 0.4978 - val_acc: 0.8615
Epoch 164/200
 - 4s - loss: 0.1852 - acc: 0.9241 - val_loss: 0.4714 - val_acc: 0.8693
Epoch 165/200
 - 4s - loss: 0.1989 - acc: 0.9194 - val_loss: 0.4584 - val_acc: 0.8814
Epoch 166/200
 - 4s - loss: 0.1785 - acc: 0.9278 - val_loss: 0.4112 - val_acc: 0.8808
Epoch 167/200
 - 4s - loss: 0.1687 - acc: 0.9325 - val_loss: 0.5136 - val_acc: 0.8522
Epoch 168/200
 - 4s - loss: 0.1928 - acc: 0.9231 - val_loss: 0.5073 - val_acc: 0.8634
Epoch 169/200
 - 4s - loss: 0.1812 - acc: 0.9241 - val_loss: 0.4673 - val_acc: 0.8617
Epoch 170/200
 - 4s - loss: 0.2066 - acc: 0.9156 - val_loss: 0.3921 - val_acc: 0.8769
Epoch 171/200
 - 4s - loss: 0.2004 - acc: 0.9256 - val_loss: 0.4375 - val_acc: 0.8693
Epoch 172/200
 - 4s - loss: 0.2010 - acc: 0.9172 - val_loss: 0.4711 - val_acc: 0.8679
Epoch 173/200
 - 4s - loss: 0.1740 - acc: 0.9322 - val_loss: 0.4917 - val_acc: 0.8602
Epoch 174/200
 - 4s - loss: 0.1916 - acc: 0.9219 - val_loss: 0.3857 - val_acc: 0.8801
Epoch 175/200
 - 4s - loss: 0.1932 - acc: 0.9191 - val_loss: 0.4196 - val_acc: 0.8686
Epoch 176/200
 - 4s - loss: 0.1666 - acc: 0.9350 - val_loss: 0.5123 - val_acc: 0.8464
Epoch 177/200
 - 4s - loss: 0.1633 - acc: 0.9369 - val_loss: 0.5603 - val_acc: 0.8628
Epoch 178/200
 - 4s - loss: 0.2012 - acc: 0.9209 - val_loss: 0.4216 - val_acc: 0.8737
Epoch 179/200
 - 4s - loss: 0.1884 - acc: 0.9216 - val_loss: 0.4573 - val_acc: 0.8679
Epoch 180/200
 - 4s - loss: 0.1740 - acc: 0.9328 - val_loss: 0.4219 - val_acc: 0.8687
Epoch 181/200
 - 4s - loss: 0.2347 - acc: 0.9109 - val_loss: 0.4681 - val_acc: 0.8563
Epoch 182/200
 - 4s - loss: 0.2275 - acc: 0.9097 - val_loss: 0.4040 - val_acc: 0.8634
Epoch 183/200
 - 4s - loss: 0.1867 - acc: 0.9281 - val_loss: 0.4513 - val_acc: 0.8629
Epoch 184/200
 - 4s - loss: 0.1978 - acc: 0.9194 - val_loss: 0.4338 - val_acc: 0.8492
Epoch 185/200
 - 4s - loss: 0.1923 - acc: 0.9178 - val_loss: 0.5077 - val_acc: 0.8591
Epoch 186/200
 - 4s - loss: 0.1890 - acc: 0.9281 - val_loss: 0.4509 - val_acc: 0.8789
Epoch 187/200
 - 4s - loss: 0.1715 - acc: 0.9313 - val_loss: 0.4852 - val_acc: 0.8471
Epoch 188/200
 - 4s - loss: 0.1886 - acc: 0.9234 - val_loss: 0.4638 - val_acc: 0.8628
Epoch 189/200
 - 4s - loss: 0.1892 - acc: 0.9269 - val_loss: 0.4202 - val_acc: 0.8860
Epoch 190/200
 - 4s - loss: 0.2118 - acc: 0.9141 - val_loss: 0.4440 - val_acc: 0.8756
Epoch 191/200
 - 4s - loss: 0.2109 - acc: 0.9134 - val_loss: 0.6252 - val_acc: 0.8486
Epoch 192/200
 - 4s - loss: 0.2013 - acc: 0.9169 - val_loss: 0.4821 - val_acc: 0.8591
Epoch 193/200
 - 4s - loss: 0.2077 - acc: 0.9087 - val_loss: 0.4113 - val_acc: 0.8705
Epoch 194/200
 - 4s - loss: 0.1982 - acc: 0.9231 - val_loss: 0.5254 - val_acc: 0.8604
Epoch 195/200
 - 4s - loss: 0.1646 - acc: 0.9303 - val_loss: 0.5425 - val_acc: 0.8718
Epoch 196/200
 - 4s - loss: 0.1997 - acc: 0.9169 - val_loss: 0.6064 - val_acc: 0.8648
Epoch 197/200
 - 4s - loss: 0.2133 - acc: 0.9113 - val_loss: 0.4741 - val_acc: 0.8537
Epoch 198/200
 - 4s - loss: 0.2109 - acc: 0.9191 - val_loss: 0.4441 - val_acc: 0.8505
Epoch 199/200
 - 4s - loss: 0.1894 - acc: 0.9253 - val_loss: 0.4461 - val_acc: 0.8534
Epoch 200/200
 - 4s - loss: 0.1711 - acc: 0.9309 - val_loss: 0.4862 - val_acc: 0.8634
seconds= 816.1493120193481

doceProcesos

tiempo en laptop ~16000 secs ~4hrs
tiempo en wks 931 secs ~15min (x17)

Salvamos el modelo y visualizamos resultados

model.save('cats_and_dogs_small_2.h5')

acc4 = history.history['acc']
val_acc4 = history.history['val_acc']
loss4 = history.history['loss']
val_loss4 = history.history['val_loss']

import numpy as np
acc     =np.concatenate([acc2, acc3, acc4])
val_acc =np.concatenate([val_acc2, val_acc3, val_acc4])

loss     =np.concatenate([loss2, loss3, loss4])
val_loss =np.concatenate([val_loss2, val_loss3, val_loss4])

acc.shape

(600,)

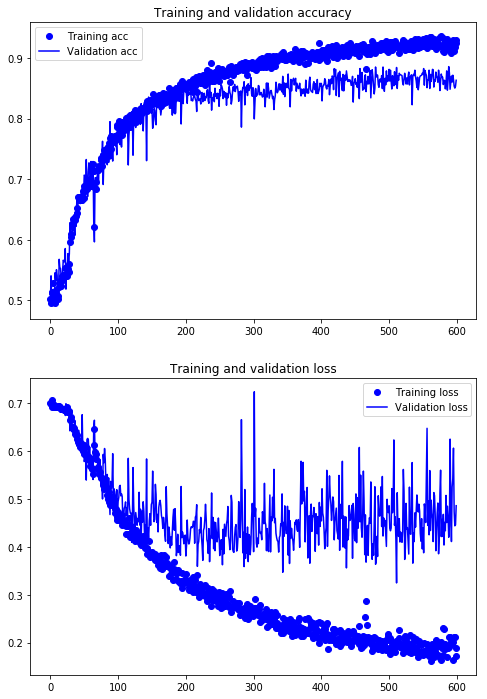
Gráfica de los resultados

epochs = range(len(acc))

plt.figure(figsize=(8,12))

plt.subplot(211)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()


plt.subplot(212)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.savefig('convnet_aug_p200epch.eps')
plt.show()

png

def smooth_curve(points, factor=0.95):
  smoothed_points = []
  for point in points:
    if smoothed_points:
      previous = smoothed_points[-1]  # last appendded value 
      smoothed_points.append(previous*factor + point*(1-factor))
    else:
      smoothed_points.append(point)   # first point 
  return smoothed_points

smooth_val_acc = smooth_curve(val_acc)
smooth_val_loss = smooth_curve(val_loss)
smooth_acc = smooth_curve(acc)
smooth_loss = smooth_curve(loss)

plt.figure(figsize=(8,12))

plt.subplot(211)
plt.plot(smooth_acc, 'bo', label='Training acc')
plt.plot(smooth_val_acc, 'b', label='Validation acc')
plt.title('Training and -smoothed- validation accuracy')
plt.legend()

#plt.savefig('convnet_aug_accuracy.eps')

plt.subplot(212)
plt.plot(smooth_loss, 'bo', label='Training loss')
plt.plot(smooth_val_loss, 'b', label='Validation loss')
plt.title('Training and -smothed- validation loss')
plt.legend()

plt.axhline(.36)
#plt.savefig('convnet_aug_loss.eps')
plt.show()

png

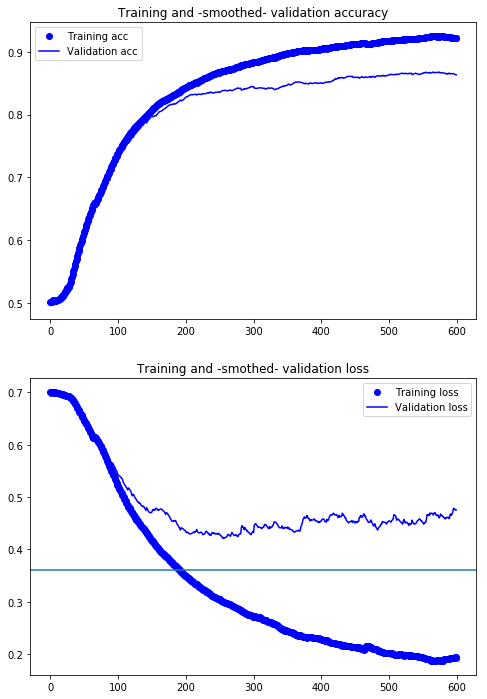
Por efectos del aumentado de datos y del dropout se ha aumentado la eficiencia de la red de un 75% a un 87%; es, aproximadamente, un 16% de mejora.

Sin embargo, aun es un valor bajo para los niveles que logramos con la DB MNIST.

val_acc[-30]

0.8692893401015228