Implementación en NUMPY de Retropropagación (Backpropagation) para un MLP simple

Licencia Creative Commons Notas Temas de Aprendizaje , Mariano Rivera, CIMAT © 2022

backpropagation

Problema: Clasificar imágenes de dos dígitos MNIST

Mariano Rivera

Versión Oct 2023

Imagen de portada generada con Stable Diffusion con el prompt: “an artistic interpretation of the backpropagation algorithm”.

Derivación del algoritmo de Backpropagation

Un Perceptrón multicapa (Multilayer Perceptrón, MLP) de una sóla capa oculta corresponde a realizar las siguientes operaciones hacia adelante:

(1)
y0=x                       z1=W1 y0+b1y1=ϕ1(z1)            z2=W2 y1+b2y2=ϕ2(z2)            y^=y2                        y_0 = x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ z_1 = W_1 \, y_0 + b_1 \\ y_1 = \phi_1 (z_1) \,\,\,\,\,\,\,\,\,\,\,\, \\ z_2 = W_2 \, y_1 + b_2 \\ y_2 = \phi_2 (z_2) \,\,\,\,\,\,\,\,\,\,\,\, \\ \hat y = y_2 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,

Dado que el problema que nos planteamos es del tipo clasificación binaria, usaremos la Entropía Cruzada Binaria como función de costo:

(2)
L(y,y^2)=−∑i[yilog⁡(y^i)+(1−yi)log⁡(1−y^i)] L(y, \hat y_2) = - \sum_i \left[ y_i \log (\hat y_i) + (1-y_i) \log(1-\hat y_i) \right]
Donde la suma la realizamos sobre todos los datos.

Entonces:

(3)
∂L∂W2=∂L∂z2   ∂z2∂W2                                =[y2−ϕ2(z2)]⊤ y1∂L∂b2=∂L∂z2   ∂z2∂b2=[y2−ϕ2(z2)]  (1) \frac{\partial L}{\partial W_2} = \frac{\partial L}{\partial z_2} \,\,\, \frac{\partial z_2}{\partial W_2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ = \left[ y_2 - \phi_2(z_2) \right]^\top \, y_{1} \\ \frac{\partial L}{\partial b_2} = \frac{\partial L}{\partial z_2} \,\,\, \frac{\partial z_2}{\partial b_2} \\ = \left[ y_2 - \phi_2(z_2) \right] \, \, (1)

(4)
∂L∂W1=∂L∂z1   ∂z1∂W1                             =∂L∂z2  ∂z2∂z1   ∂z1∂W1                              =[y2−ϕ2(z2)]⊤ W2  ϕ′(z1) y0∂L∂b1=∂L∂z2   ∂z2∂z1   ∂z1∂b1                                              =[y2−ϕ2(z2)]⊤ W2  ϕ′(z1) (1) \frac{\partial L}{\partial W_1} = \frac{\partial L}{\partial z_1} \,\,\, \frac{\partial z_1}{\partial W_1} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ = \frac{\partial L}{\partial z_2} \,\, \frac{\partial z_2}{\partial z_1} \,\,\, \frac{\partial z_1}{\partial W_1} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left[ y_2 - \phi_2(z_2) \right]^\top \, W_2 \,\, \phi'(z_1) \, y_{0} \\ \frac{\partial L}{\partial b_1} = \frac{\partial L}{\partial z_2} \,\,\, \frac{\partial z_2}{\partial z_1}\,\,\, \frac{\partial z_1}{\partial b_1} \,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= \left[ y_2 - \phi_2(z_2) \right]^\top \, W_2 \,\, \phi'(z_1) \, (1)

Los detalles de  ∂L/∂z2 \,{\partial L}/{\partial z_2}\, se presentan en el Apéndice, al final de estas notas. Para una derivación mas general ver Redes Multicapa y el algoritmo de Backpropagation

Luego, implementaremos el algoritmo de Descenso de gradiente simple sobre todo el conjunto de entrenamiento para actualizar los parámetros: W1,W2,b1W_1, W_2, b_1 y b2b_2. Por ejemplo:

(5)
θt+1=θt−α∂L∂θt. \theta^{t+1} = \theta^{t} - \alpha \frac{\partial L}{\partial \theta^{t}}.

En nuestra implementación usaremos la sigmoide como función de activación:

(6)
ϕ(z)=11+exp⁡(−z) \phi(z) = \frac{1}{1+\exp(-z)}
cuya derivada es ϕ′(z)=ϕ(z)[1−ϕ(z)]\phi'(z) = \phi(z) [1-\phi(z)]; ver Apéndice.

Ejemplo de aplicación

import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split

Cargar la base de datos MNIST

mnist = fetch_openml("mnist_784")
X, y = mnist.data, mnist.target.astype(int)

# Seleccion de solo imagenes de dígitos 0 y 1
X = X[(y == 0) | (y == 1)]
y = y[(y == 0) | (y == 1)]

# Separar en conjuntos de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Normalizar datos
X_train = X_train / 255.0
X_test  = X_test  / 255.0

# dimensiones de los conjuntos
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)

(11824, 784) (11824,)
(2956, 784) (2956,)

Función de activación

def phi(x):
    return 1 / (1 + np.exp(-x))

Inicializar pesos y biases

input_size = X_train.shape[1]
hidden_size = 64
output_size = 1

#np.random.seed(0)  # descomentar si queremos replicar el entrenamiento
W_1 = 0.1*np.random.randn(input_size, hidden_size,)
b_1 = 0.1*np.zeros((1, hidden_size))
W_2 = 0.1*np.random.randn(hidden_size,output_size,)
b_2 = 0.1*np.zeros((1,output_size))

Parámetros de entrenamiento

learning_rate = 1e-4
epochs = 30

Ciclo de entrenamiento

Cada ciclo de entrenamiento consiste en realizar los siguientes pasos:

  1. Evaluar la el preceptrón multicapa (modelo) con los datos en el lote actual. A este paso se denomina Propagación hacia adelante.
  2. Evaluar la función de pérdida.
  3. Calcular las derivadas del modelo respecto a sus parámetros. Paso de Retropropagación, pues reusa parte de los cálculos obtenidos en el paso 1.
  4. Ajustar los parámetros del modelo con el algoritmo de aprendizaje

Estos pasos se repiten hasta que alcance el criterio de paro (por iteraciones o por magnitud del gradiente). La implementacion en numpy se presenta a continuación.

Nota. En nuestros cálculos usamos las operaciones con forma de transpuesta y⊤W⊤y^\top W^\top en vez de la estándar WyW y dado que la primera emplea los datos en su formato original y simplifica la implementación.

y_0 = X_train
y   = np.expand_dims(y_train, axis=-1)

Losses=[]
for epoch in range(epochs):
    # Propagación hacia adelante, Eqs. (1)
    z_1 = y_0 @ W_1 + b_1
    y_1 = phi(z_1)
    z_2 = y_1 @ W_2 + b_2
    y_2 = phi(z_2)
    
    # Evaluar la pérdida, Eq. (2)
    loss = -np.mean(y * np.log(y_2) + (1 - y) * np.log(1 - y_2))

    # Backpropagation, Eqs. (3) y (4)
    delta_2 = y_2-y
    delta_1 = np.dot(delta_2, W_2.T) * (y_1*(1-y_1))
    grad_W2 = np.dot(y_1.T, delta_2)
    grad_b2 = np.sum(delta_2)[0]
    grad_W1 = np.dot(y_0.T, delta_1)
    grad_b1 = np.sum(delta_1)[0]

    # Paso de descenso de gradiente, Eq. (5)
    W_2 -= learning_rate * grad_W2
    b_2 -= learning_rate * grad_b2
    W_1 -= learning_rate * grad_W1
    b_1 -= learning_rate * grad_b1

    # Reporta avence cada 1 épocas
    if epoch % 1 == 0:
        print(f"Epoch {epoch}, Loss: {loss}")
        Losses.append([epoch,loss])

Losses = np.array(Losses)

Epoch 0, Loss: 0.7805168192126555
Epoch 1, Loss: 1.8910299637556995
Epoch 2, Loss: 2.516437887729284
Epoch 3, Loss: 0.3938748583958368
...
Epoch 28, Loss: 0.018629451129235922
Epoch 29, Loss: 0.018139000372665838

import matplotlib.pyplot as plt

plt.figure(figsize=(10,3))
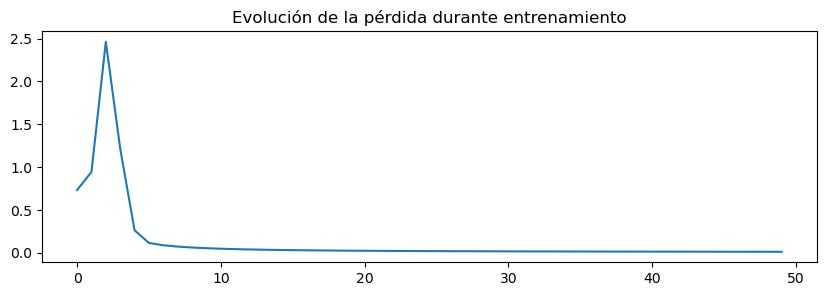
plt.plot(Losses[:,0],Losses[:,1])
plt.title('Evolución de la pérdida durante entrenamiento')

Text(0.5, 1.0, 'Evolución de la pérdida durante entrenamiento')

png

Prueba

z_1 = X_test @ W_1 + b_1
y_1 = phi(z_1)
z_2 = y_1 @ W_2 + b_2
y_2 = phi(z_2)

# Convierte predicciones a probabilidades 
predictions = np.squeeze((y_2 >= 0.5).astype(int))
y_test      = np.array(y_test)

# Calcula Exactitud: porcentaje de clasificaciones correctas
accuracy = np.mean(predictions == y_test)
print(f"Exactitud de Prueba (Test accuracy): {accuracy * 100}%")

Exactitud de Prueba (Test accuracy): 99.86468200270636%

Ejercicios Recomendados

  1. Complete la derivación para un perceptrón multicapa; con k>1 capas ocultas.
  2. Ensaye con otras funciones de activación y use distintas para ϕ1\phi_1 y ϕ2\phi_2.
  3. Implemente una estrategia de descenso estocástico.
  4. Evalué con otros algoritmos de entrenamiento; p.ej. Nesterov y Adam.
  5. Generalice el clasificador para mas clases de imágenes de dígitos: las diez clases en MNIST.

Apéndice. Derivada de la función de costo, Eq. (2)

L(y,y^2)=∑il(ϕ([z2]i);yi). L(y, \hat y_2) = \sum_i l(\phi([{z_2}]_i); y_i).
Luego

∂∂zl(ϕ(z);y)=−∂∂z[y log⁡(ϕ(z)))+(1−y) log⁡(1−ϕ(z))]  =−yϕ(z)ϕ′(z)+(1−y)ϕ′(z)1−ϕ(z)        =−y[1−ϕ(z)]+(1−y)ϕ(z)                        =−y+y ϕ(z)+ϕ(z)−y ϕ(z)              =ϕ(z)−y.                                                        \frac{\partial}{\partial z} l(\phi({z}); y) = - \frac{\partial}{\partial z} \left[y \, \log (\phi(z) )) + (1-y) \, \log( 1-\phi(z) ) \right] \\ \,\, = - \frac{y}{\phi(z)} \phi^\prime(z)+ (1-y) \frac{\phi^\prime(z)}{1-\phi(z)} \\ \,\,\,\,\,\,\,\,= - y [1-\phi(z)] + (1-y) \phi(z) \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \,\,\,\,\,\,\,\, = - y + y\,\phi(z) + \phi(z)- y \,\phi(z) \,\,\,\,\,\,\, \,\,\,\,\,\,\, \\ = \phi(z)-y. \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,
Donde hemos usado
∂ϕ(z)∂z=∂∂z11+e−z                                   =e−z(1+e−z)2                                            =(11+e−z) (1+e−z−11+e−z)                                          =(11+e−z) (1+e−z1+e−z−11+e−z)=ϕ(z)[1−ϕ(z)].        \frac{\partial \phi(z)}{\partial z} = \frac{\partial}{\partial z} \frac{1}{1+e^{-z}} \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \\ = \frac{e^{-z}}{\left(1+e^{-z}\right)^2} \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\\ \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\, = \left(\frac{1}{1+e^{-z}}\right) \, \left( \frac{1+ e^{-z} -1}{1+e^{-z}} \right) \\ \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, \,\,\,\,\,\,\, = \left(\frac{1}{1+e^{-z}}\right) \, \left( \frac{1+ e^{-z}}{1+e^{-z}} -\frac{1}{1+e^{-z}} \right) \\ = \phi(z) \left[1-\phi(z) \right]. \,\,\,\,\,\,\,