Redes Neuronales Artificiales

Mariano Rivera

Mayo 2017

Haremos una revisión rápida de los modelos

1. Perceptrón

2. Red de una capa: Neurona Lineal Adaptativa o ADAptive LInear NEuron (ADALINE)

3. La Multicapa

En cada caso revisaremos su algoritmo de entrenamiento

El Perceptrón

• Basado en el modelo de la neurona de McCulloc-Pitts (MCP) (1943) [1].

• Rosenblatt propone la regla de aprendizaje basada en modelo de neurona MCP [2]

• El algoritmo propuesto por Rosenblatt (1957), puede automáticamente aprender los pesos (coeficientes) óptimos que multiplican a las variables de entrada y tomar la desición de si se activa o no una neurona.

[1] W. S. McCulloc and W.Pitts, A logical calculus o the ideas immanent in neuron activity, The Bulletin of the Mathematical Biophysics, 5(4) 115-133, 1943.

[2] F. Rosenblatt. “The Perceptron, a perceiving and recognizing automaton,” Cornell Aeronautical Lab, 1957

El modelo MCP de la neurona explica que:

1. Las señales se ingresan a la neuraona a través de la dendrita.

2. Se integran en el cuerpo (soma) de la neurona.

3. Si la señal acumulada sobrepasa un umbral, la neurona se activa y dispara una señal a través de al axón

4. A su vez, el axón se conecta a otras neuronas.

Considere la siguiente figura, en ella se muestra el modelo de la neurona MCP (Basada en la figura de neurona de Wikipeda)

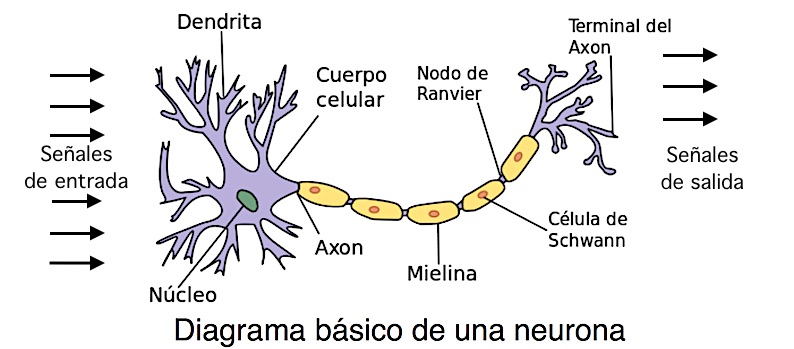
Rosemblatt propone el concepto de la Regla de Aprendizaje del Perceptrón basada en el modelo de la neurona de MCP.

Sean $\mathbf{x} \in \mathbb{R}^n$ representa los un dato en coordenadas homogéneas (le hemos añadido un 1 al frente) y $\mathbf{w} \in \mathbb{R}^n$ el vector de coeficientes:

(1)
$\mathbf{x} = \begin{bmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_{n-1} \end{bmatrix}, \;\;\;\; \;\;\;\; \mathbf{w} = \begin{bmatrix} w_0 \\ w_1 \\ w_2 \\ \vdots \\ w_{n-1} \end{bmatrix}$

Tal que $\mathbf{x}_i \in \mathbb{R}^n$ es el $i$-ésimo dato, para $i= 1,2,\ldots,m$ con ${y}_i \in \{-1,+1 \}$ la clase es el $i$-ésimo dato, para $i= 1,2,\ldots,m$.

Luego, denotamos el producto interior por

(2)
$\mathbf{z} = \mathbf{w}^\top \mathbf{x}$
y la neurona se activará (preferirá la clase $+1$) si el producto es mayor que cero, en otro caso no se activará (predecirá la clase $-1$):

(3)
$\phi(\mathbf{z}) \overset{def}{=} \left\{ \begin{matrix} +1 & z \ge 0 \\ -1 & \text{otro} \end{matrix} \right.$

---

Algoritmo del Perceptrón

Sean ($\mathbf{x}_i, y_i)$ pares de dato y su respectiva clase, para $i= 1,2,\ldots,m$. Luego

1. Inicialice los pesos $w$ con valores aleatorios pequeños: $|w_j| \approx 0$ para $j=1,2,\ldots,n$.

2. Iterar para $i=1,2,\ldots, m$ (para todas las muestras)

$\;\;\;\;\;\;\;\;$ 2.1 Calcular la salida

(4)
$y'_i = \phi(\mathbf{w}^\top \mathbf{x}_i)$
$\;\;\;\;\;\;\;\;$ 2.1 Actualizar el vector de peso

(5)
$\mathbf{ w} \leftarrow \mathbf{ w} + \alpha \, ( y_i - y'_i )\,\mathbf{x}_i$
$\;\;\;\;\;\;\;\;\;\;\;\;$ donde $\alpha$ es conocida como la razón de aprendizaje.

---

La idea de la regla de aprendizaje del perceptrón es muy básica:

• Se presentan las muestras y si la respuesta no coincide se hace la corrección agregando una fracción de dato a los pesos.

• tendremos una alta coincidencia cuando:

$\;\;\;\;\;\;\;\; \mathbf{w}^\top \mathbf{x}_i >0$ si $y_i =+1$

$\;\;\;\;\;\;\;\; \mathbf{w}^\top \mathbf{x}_i <0$ si $y_i =-1$

En la siguiente figura, se muestra un vector $\mathbf{w}$ que satisface la respuesta correcta para todos los puntos.

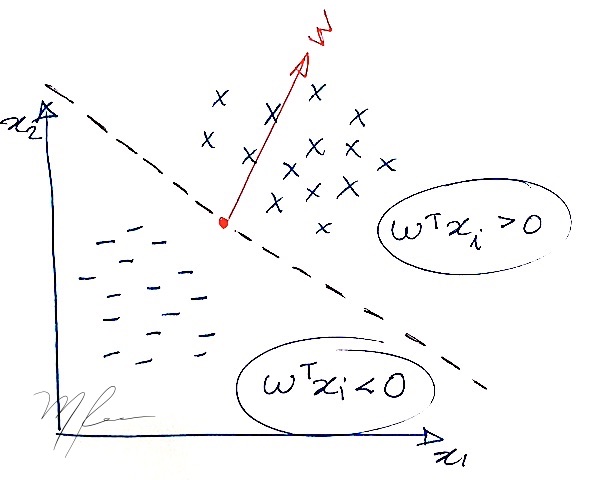
En la ilustración de la figura anterior, ${\bf w}^\top x$ es un plano que intersecta el plano de los datos en la línea punteada. Ajustar el valor de $w_0$ corresponde gráficamente a modificar el origen del vector $\mathbf{w}$.

Neurona Lineal Adaptable

ADALINE: ADAptive LInear NEuron

• La variante ADALINE del perceptrón fué propoesto por Widrow & Hoff [3].

• Es particularmente importante porque introcude el concepto clave de definir mi minimixaruna función de costo.

• Conceptos claves de algoritmos avanzados de “Aprendizaje de Máquina”.

• A diferencia del Perceptrón usa una función de activación lineal:

(6)
$\phi_{WH}(\mathbf{w}^\top \mathbf{x}_i) \overset{def}{=} \mathbf{w}^\top \mathbf{x}_i$

• Un cuantizador es utilizado después para de la etapa de entrenamiento para dar la respuesta binaria

[3] B. Widrow and T Hoff, An Adaptive “Adaline” Neuron using Chemical “Memistors”, Nu. Tech. Rep. 1553-2, Stanford Electron. Labs., Stanford CA, Oct, 1960.

Gráficamente, el concepto de la ADALINE se puede ver en la siguiente figura

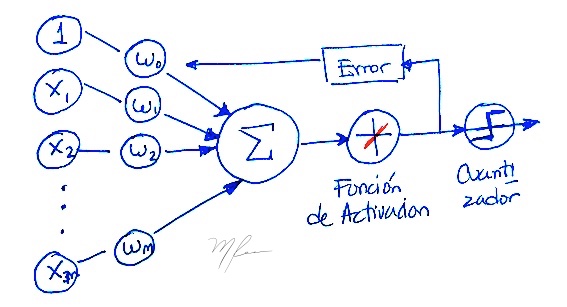
Función de costo ADALINE

La función de costo de ADALINE como sigue:

(7)
$\mathbf{w}^* = \underset{\mathbf{w}}{\arg \min} \; J(\mathbf{w}) = \frac{1}{2} \sum_i \left[ y_i - \phi(\mathbf{w}^\top \mathbf{x}_i) \right]^2$

Esto nos hace recordar de donde vienen la notación de la regresión logística, pero esa regresión fué mucho tiempo después.

Desceso de Gradiente

Para resolver (7) se popuso usar Desceso de gradiente simple, con la regla de actualización:

(8)
$\mathbf{w} \leftarrow \mathbf{w} - \alpha \nabla J(\mathbf{w})$

donde $\alpha$ es el tamaño de paso y

(9)
$\nabla J(\mathbf{w}) = \begin{bmatrix} \frac{\partial }{\partial {w_0} } J(\mathbf{w}) \\ \frac{\partial }{\partial {w}_1} J(\mathbf{w}) \\ \vdots \\ \frac{\partial }{\partial {w}_{n-1}} J(\mathbf{w}) \end{bmatrix}$
con
(10)
$\frac{\partial }{\partial w_j} J(\mathbf{w}) = \sum_i \left[ y_i - \phi(\mathbf{w}^\top \mathbf{x}_i) \right] x_{ij}$

donde

• $w_j$ es el peso $j$-ésimo peso
• $x_{ij}$ es la entrada $j$-ésima del dato $i$-ésimo

En los 1950’s el interés por las redes neuronales empezó a decrecer a medida que se veia su limitación para resolver problemas complejos.

• Se vió que ADALINE y variantes con función sigmoide de activación tipo sigmoide (“REGRESIÓN LOGÍSTICA”) eran separadores lineales.

• Un separador lineal usará un hiperplano como frontera entre clases.

• Los clasificadores lineales:

$\;\;\;\;$- No prodrán distinguir entre clases que no sean-linealmente separables

$\;\;\;\;$- No podrán aprender el patrón del “famoso” problema del XOR

$\;\;\;\;$- No podrán distinguir entre clases anidadas

La figura siguiente figura ilustra casos de clasese no linelamente separables y el patrón del XOR

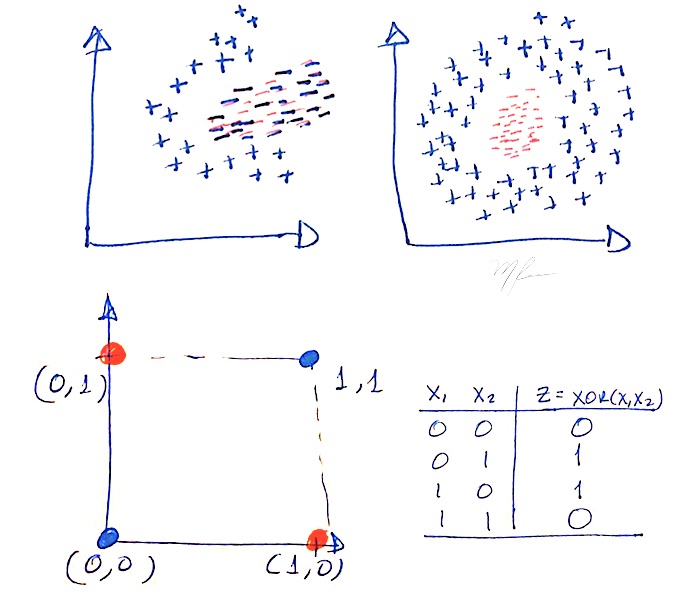
El problema es

• Agregar mas capas lineales sigue manteniedo el clasificador lineal:

Considere la primera capa del diagrama de la red multicapa lineal:

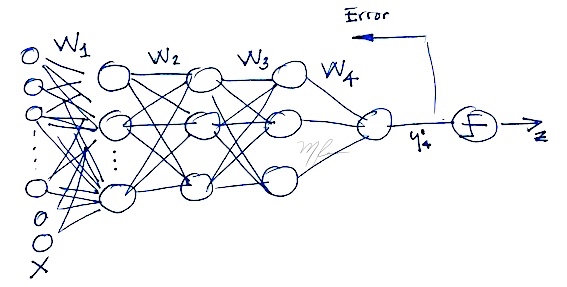
Primera capa:

(11)
$y'_{1k} = \mathbf{w}_{1k}^\top x \;\;\;\text{para}\;\; k = 1,2,3, K \\$
En forma matricial

(12)
$\mathbf{y}_1 = W_1 x$
Segunda capa:

(13)
$\mathbf{y}_2 = W_2 \mathbf{y}_1$
y para la cuarta capa tendremos:

(14)
$\mathbf{y}'_4 = W_4 \mathbf{y}_3 = W_4 W_3 W_2 W_1 \mathbf{x} = W \mathbf{x}$

donde

(15)
$\mathbf{y}'_4 = W_4 W_3 W_2 W_1 \mathbf{x} = W \mathbf{x}$

• No se sabia como entrenar clasificadores no-lineales:

(16)
$\mathbf{y}'_4 = \Phi\left(W_4 \Phi\left(W_3 \left( \Phi \left(W_2 \Phi(W_1 \mathbf{x} ) \right) \right) \right) \right)$

Redes Multicapa y el algoritmo de Backpropagation

La 2a. Generación de las Redes Neuronales

Hasta el trabajo de Rumelhart, Hinton & Williams (1986) [4] donde proponen el algoritimo de Retropropagación (Backpropagation) para entrenar redes neuronales multicapa.

[4] Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986) Learning representations by back-propagating errors. Nature, 323, 533–536.

Representaremos a una neurona con un nodo

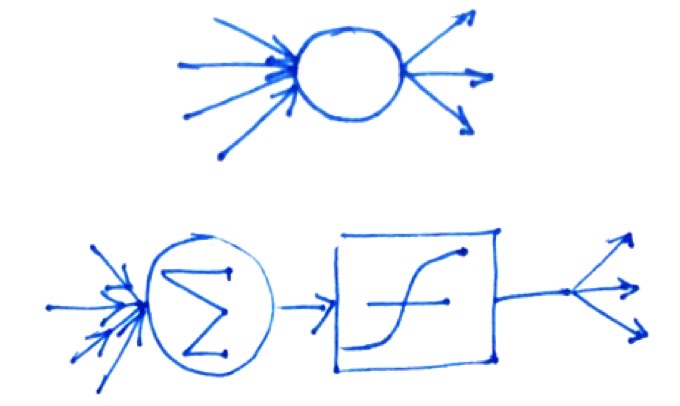
Una red completa con una capa de entrada, capa oculta y capa de salida se muestra en la figura siguente

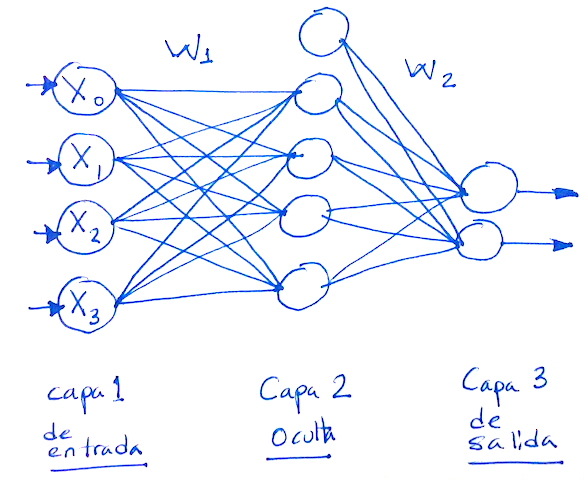
Propagación hacia adelante (Forward-propagation)

En la primera capa

(17)
$\mathbf{z}_1 = W_1 \mathbf{x}$
La matriz $W$ es de dimensión $n_1 \times n$, donde

• el número de renglones $n_1$ es neuronas de la capa oculta y
• el número de comumnas $n$ es el número de neuronas en la capa anterior.

Luego pasa a la función de activación:

(18)
$\mathbf{y}_1 = \phi ( \mathbf{z}_1 )$
donde $\phi$ es vectorial (se aplica elemento a elemento) y que se aplica a cada elemento del vector $\mathbf{y}_1$. Resultando en un vector de la misma dimensión (el número de neuronas de la capa oculta).

En la segunda capa

(19)
$\mathbf{z}_2 = W_2 \mathbf{y}_1$
La matriz $W$ es de dimensión $n_2 \times n_1$, donde

• el número de renglones $n_2$ es neuronas de la capa de interés
• el número de comumnas $n_1$ es el número de neuronas en la capa anterior.

Luego pasa a la función de activación:

(20)
$\mathbf{y}_2 = \phi ( \mathbf{z}_1 )$

Pasando de una Muestra a n Muestras

La propagacición hacea adelante que revisamod la hicimos para un dato $\mathbf{x}$.

Ahora consideremos que propagamos hacia a adelante toda la muestra $\mathbf{X}$.

Definamos
$\mathbf{Y}_0 \overset{def}{=} (\mathbf{X})^T$
Note que los datos estan ordenados por columna.

• La integración a la capa $i$-ésima se calcula

(21)
$\mathbf{Z}_{i+1} = W_{i+1} \mathbf{Y}_i$

• Activación (elemento a elemento)

(22)
$\mathbf{Y}_{i+1} = \phi(\mathbf{Z}_{i+1})$

Entrenamiento de una Red Múlticapa

• Asumamos que la capa de salida es la $k$.

• Luego, el dato (vector) $\mathbf{x}$ se propaga a través de la red y resulta en el vector de salida $\mathbf{y}_k$. El cual en la etapa anterior

se obtuvo de aplicar la función de activación: $\phi(\mathbf{z}_k)$

donde previamente $\mathbf{z}_k$ se calculó con
$\mathbf{z}_k = \mathbf{W}_k^\top \mathbf{y}_{k-1}$

donde $\mathbf{W}_k$ denota la matriz de pesos de la capa (de salida) $k$,

cuyo elemento $[\mathbf{w}_{pq}]_k$ es el peso de la salida de la neurona $p$ en la capa $k-1$ a la neurona $q$ en la capa $k$

Propagacion hacia adelante de un dato

Integración en la primera capa.

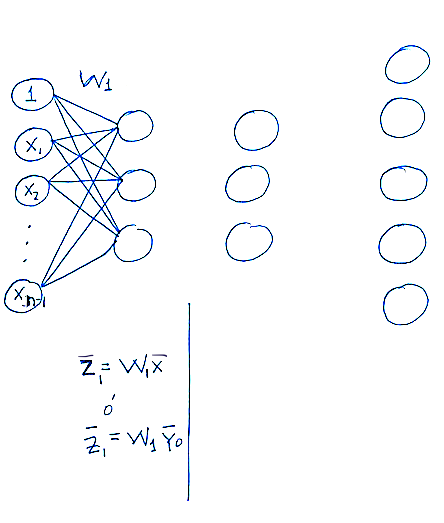
Activación de la primera capa.

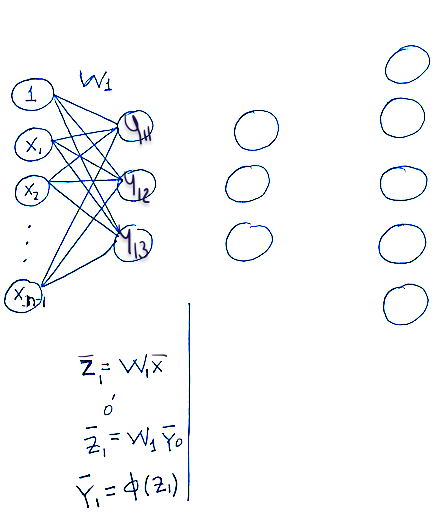
Propagación de la segunda capa

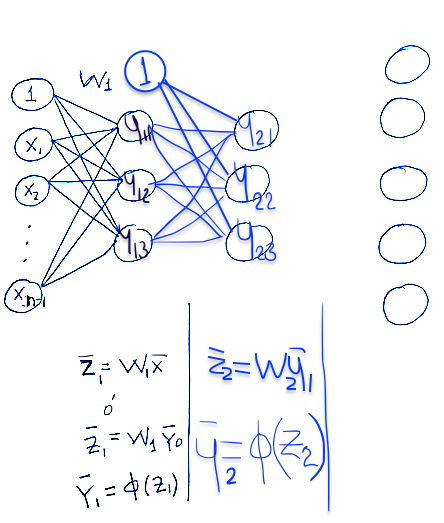
Propagación de la tercera capa

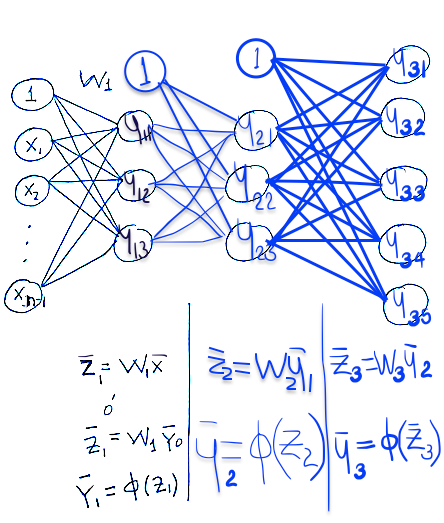
Función de Costo

Similar a la REGRESIÓN LOGISTICA, consideremos el costo en la etapa de salida

(23)
$J(\mathbf{W}) = \frac{1}{2} \sum_i \left[ \mathbf{y}'_i \,\log ([\mathbf{y}_k]_i) + (1-\mathbf{y}'_i) \, \log (1-[\mathbf{y}_k]_i) \right]$

donde $\mathbf{y}'$ es el la salida deseada para el dato $\mathbf{x}$; recodemos que estamo en etapa de entrenamiento y hemos usamos como función de activación la Función Logística:

(24)
$\phi(z) = \frac{1}{1+ e^{-z}}$
que tienen forma de “S”.

Esta función de costo se conoce como la “entropía cruzada” o “cross-entropía” y se obtienen de la log-verosimilitud al asumir residuales con distribución Bernulli.

Elementos del gradiente c.r.a. los pesos de la capa de de salida

Tomando el gradiente, obtenemos las parciales, que es exactamente igual a la derivada parcial (10):

(25)
$\frac{\partial J(\mathbf{W})}{\partial [\mathbf{w}_{k}]_{pq}} = \left[ \mathbf{y}'_k - \phi(\mathbf{z}_k) \right] [\mathbf{y}_{k-1}]_{pq}$
donde

• $[\mathbf{y}_{k-1}]_{pq}$ es la salida de la capa $k-1$, neurona $p$ que va a la neurona $q$ de la capa $k$

---

Notemos que (25) tienen la forma de la regla de la cadena:

(26)
$\frac{\partial J(\mathbf{W})}{\partial [\mathbf{w}_{k}]_{pq}} = \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k}} \; \frac{\partial \mathbf{z}_{k}}{\partial [\mathbf{w}_{k}]_{pq}}$
con

(27)
$\delta_k \overset{def}{=} \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k}} = \mathbf{y}'_k - \phi(\mathbf{z}_k)$

(28)
$\frac{\partial \mathbf{z}_{k}}{\partial [\mathbf{w}_{k}]_{pq}} = [\mathbf{y}_{k-1}]_{pq}$
Dada la forma de la primera derivada parcial (27), a $\delta_k$ se le denomina “error”.

---

En la siguiente figura se muestra el caso de k=3.

Neurona en la capa oculta anterior, que tiene como salida $y_{22}$

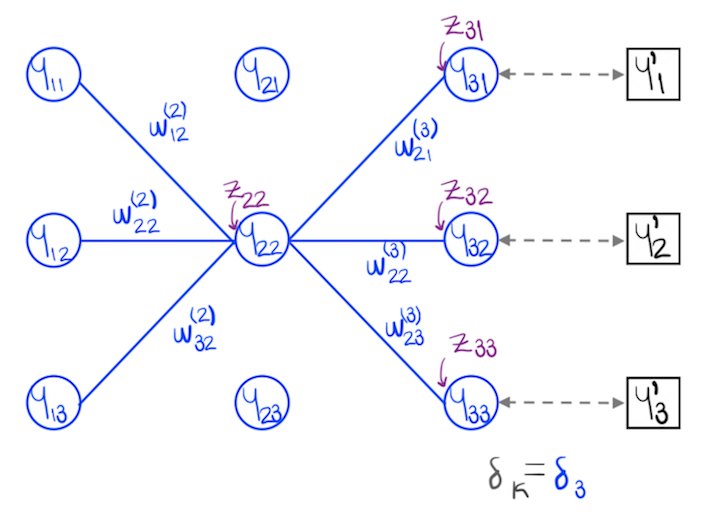
Cálculo de los demás elementos del gradiente

Las ecuaciones (25)-(28) muestran como calcular las derivadas parciales de las fucniín de costo (elementos del gradiente) c.r.a. los pesos de la capa de salida.

Para poder entrenar la red, necesitamos calcular el gradiente también en los pesos de las capas ocultas. Es decir, calcular las parciales:
$\frac{\partial J(\mathbf{W})}{\partial [\mathbf{w}_{l}]_{pq}} \;\;\;\;\text{ para }\;\;\;\; l=1,2,\ldots,k-1, \forall (p,q)$

Elementos del gradiente en la penúltima capa (última oculta)

Usando las forma de la regla de la cadena

(29)
$\frac{\partial J(\mathbf{W})}{\partial [\mathbf{w}_{k-1}]_{pq}} = \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k-1}} \, \frac{\partial \mathbf{z}_{k-1}}{\partial [\mathbf{w}_{k-1}]_{pq}}$

con

(29)
$\delta_{k-1} \overset{def}{=} \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k-1}}$

(31)
$\frac{\partial \mathbf{z}_{k-1}}{\partial [\mathbf{w}_{k-1}]_{pq}} = [\mathbf{y}_{k-2}]_{pq}$
Ahora, para calcular $\delta_{k-1}$ usamos de nuevo la regla de la cadena

(32)
$\delta_{k-1} = \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k}} \, \frac{\partial \mathbf{z}_{k}}{\partial \mathbf{z}_{k-1}} = \, \delta_k^\top \, \mathbf{W}_{k-1} \, \phi' ( \mathbf{z}_{k-1} )$

Para obtener $\frac{\partial \mathbf{z}_{k}}{\partial \mathbf{z}_{k-1}}$ usamos:

${\bf z}_{k} = \begin{bmatrix} {z}_{k,1} \\ {z}_{k,2} \\ \vdots \\ {z}_{k,N} \end{bmatrix} = \begin{bmatrix} {\bf w}_{k-1,1}^\top {\bf y}_{k-1} \\ {\bf w}_{k-1,2}^\top {\bf y}_{k-1} \\ \vdots \\ {\bf w}_{k-1,N}^\top {\bf y}_{k-1} \end{bmatrix} = \begin{bmatrix} {\bf w}_{k-1,1}^\top \phi ( {\bf z}_{k-1} ) \\ {\bf w}_{k-1,2}^\top \phi ( {\bf z}_{k-1} ) \\ \vdots \\ {\bf w}_{k-1,N}^\top \phi ({\bf z}_{k-1} ) \end{bmatrix} = {\bf W}_{k-1} \phi ( {\bf z}_{k-1} )$

entonces

(33)
$\frac{\partial \mathbf{z}_{k}}{\partial \mathbf{z}_{k-1}} = \mathbf{W}_{k-1} \, \phi' ( \mathbf{z}_{k-1} )$

Elementos del gradiente en la Ante-Penúltima capa

Usando las forma de la regla de la cadena

(34)
$\frac{\partial J(\mathbf{W})}{\partial [\mathbf{w}_{k-2}]_{pq}} = \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k-2}} \, \frac{\partial \mathbf{z}_{k-2}}{\partial [\mathbf{w}_{k-2}]_{pq}}$
con

(35)
$\delta_{k-2} \overset{def}{=} \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k-2}}$

(36)
$\frac{\partial \mathbf{z}_{k-2}}{\partial [\mathbf{w}_{k-2}]_{pq}} = [\mathbf{y}_{k-3}]_{pq}$

Ahora, para calcular $\delta_{k-1}$ usamos de nuevo la regla de la cadena

(37)
$\delta_{k-2} = \frac{\partial J(\mathbf{W})}{\partial \mathbf{z}_{k-1}} \, \frac{\partial \mathbf{z}_{k-1}}{\partial \mathbf{z}_{k-2}} = \, \delta_{k-1}^\top \, \mathbf{W}_{k-2} \, \phi' ( \mathbf{z}_{k-2} )$

Una vez calculado $\nabla_{\bf W} J^{(i)}$ para el dato $(x_i, y_i)$ se actualizan los pesos:

(38)
$w^{t+1} = w^t - \alpha \nabla_{\mathbf{W} }J^{(i)}$