Arquitecturas de Rede Neuronales con Múltiples Ramas
Introducción al API de Keras
Mariano Rivera
noviembre 2018
Muchas arquitecturas de redes neuronales se pueden visualizar con una secuencia de módulos que se ejecutan una tras otro hasta
que se arroja una salida. Es decir, aunque se empleén módulos recursivos e inclusive recursivos bidireccionales, si obviamos la estructura interna de dichos módulos, la red se conforma por una pila de módulos que procesan la salida del módulo previo y cuya salida es procesada por el siguiente módulo hasta alcanzar la salida de la NN, ver la siguiente figura.
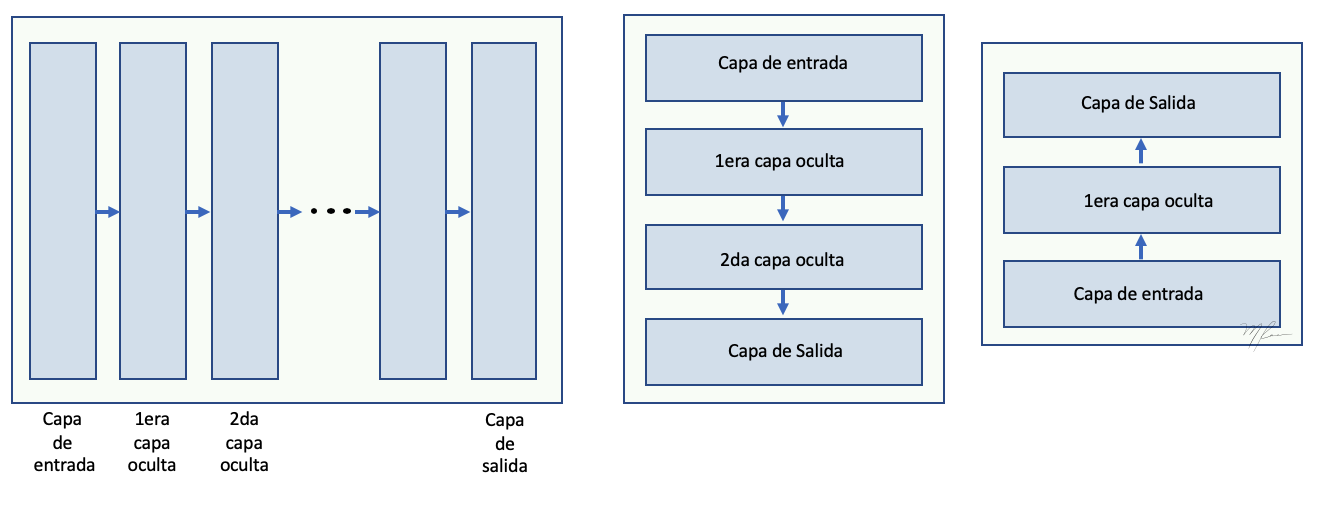
Sin embargo, resulta que en muchas ocasiones es necesario implementar arquitecuras de NN complejas que nos permitan procesar varias entradas y cuya naturaleza sea tan distinta que no resulte apropiado trabajar con una concatenación de los datos, sino procesar las entradas mediante distintar ramas y previamente a la salida unir los resultados parciales para arrojar una salida que consence los procesamientos de las ramas. Para implementar dichas arquitecturas complejas aremos primeramente un introducción breve de la API de Keras.
Keras y Keras-API
Keras
Asumamos una red multicapa secuencial como la de la figura anterior de tres capas (layers), con un vector de entrada de tamalo 64 y número de neuronas (unidades) por capa dadas por la lista [32, 32, 10]. Probablemente esta red nos permita distinguir entre dígitos en imágenes de .
Primero importanmos las funciones requeridas de Keras
from keras import Sequential, Model
from keras import layers
Ahora, desarrollamos la arquitectura propia de nuestra NN y desplegamos el resumen de la misma.
seq_model = Sequential()
seq_model.add(layers.Dense(32, activation='relu', input_shape=(64,)))
seq_model.add(layers.Dense(32, activation='relu'))
seq_model.add(layers.Dense(10, activation='softmax'))
seq_model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_26 (Dense) (None, 32) 2080
_________________________________________________________________
dense_27 (Dense) (None, 32) 1056
_________________________________________________________________
dense_28 (Dense) (None, 10) 330
=================================================================
Total params: 3,466
Trainable params: 3,466
Non-trainable params: 0
_________________________________________________________________
Es un red típica de 3,466 parámetros, todos entrenables.
Keras API
from keras import Sequential, Model
from keras import layers
from keras import Input
Para definir la NN usando la API de Keras, es necesario incluir una nueva función: Input. La cuál define que tensor, o tensores, será usado como entrada a red y especificar su forma; recordemos que el tamaño del lote se define al realizar el entrenamiento, por lo que aquí no es necesario especificar.
input_tensor=Input(shape=(64,))
Agregando las capas (layers) con la API.
Diferente a como se añaden las capas en la forma simple de Keras, donde el método
add
asume que
-
la entrada a la primera capa se define por el parámetro input de la función de entrenamiento (
fit) y -
cada nueva capa usa como entrada la salida de la anteriormente capa añadida (cuyo tamaño se define por el número de unidades).
Con el API, es necesario indicar el flujo de los tensores. La forma en que se define una capa usa el siguiente formato
tensor_salida = layers.Dense(units=num_unidades,
activation = 'funcion_activacion',
input_shape=(*shape*)) (tensor_entrada)
para nuestro ejemplo, esto corresponde a
model = Model(inputs=[main_input, auxiliary_input], outputs=[main_output, auxiliary_output])
x=layers.Dense(units=32, activation='relu') (input_tensor)
x=layers.Dense(units=32, activation='relu') (x)
output_tensor=layers.Dense(10, activation='softmax') (x)
Ahora, hemos definido las capas. La creación de capas establecida por el orden de ejecución de Python implica que el tensor de salida de la primera capa (x) es la entrada a la segunda capa, que la salida de la segunda capa (también denotadad por x) es la entrada a la última capa, con salida output_tensor.
Sin embargo, pudimos ser mas explícitos y para evitar cualquier confusión entre las x's podemos usar
in_tensor=Input(shape=(64,))
x1 = layers.Dense(units = 32, activation = 'relu') (in_tensor)
x2 = layers.Dense(units = 32, activation = 'relu') (x1)
out_tensor=layers.Dense(units=10, activation='softmax') (x2)
Hasta ahora tenemos capas conectadas, pero no aun un modelo entrenable. En cualquiera de los casos mostrados, es necesario definir un modelo la entrada (o entradas) y la salida (o salidas); esto es, a que capa se alimentan los datos y en que salida se mide el error (función de pérdida).
Para ello usamos
model = Model(inputs=[main_input, auxiliary_input], outputs=[main_output, auxiliary_output])
donde los parámetros
inputs: es el tensor (o lista de tensores) datos
outputs: es el tensor (o lista de tensore) resultados
En nuestro caso, queda como
model_sequential=Model(in_tensor, out_tensor)
model_sequential.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_7 (InputLayer) (None, 64) 0
_________________________________________________________________
dense_32 (Dense) (None, 32) 2080
_________________________________________________________________
dense_33 (Dense) (None, 32) 1056
_________________________________________________________________
dense_34 (Dense) (None, 10) 330
=================================================================
Total params: 3,466
Trainable params: 3,466
Non-trainable params: 0
_________________________________________________________________
# Visualización
from keras.utils import plot_model
plot_model(model_sequential, to_file='model_sequential.png',show_shapes=True, show_layer_names=True)
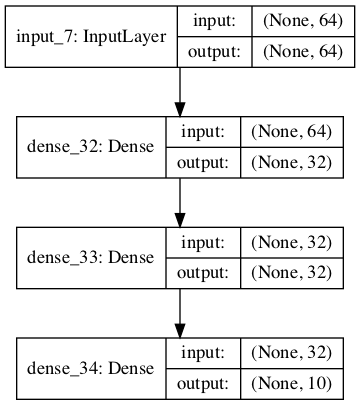
Que contienen exactamente los mismos parámetros que el modelo que usa la forma simple, de Keras.
Capas (Layers) de operaciónes con múltiples entradas y una salida
A continuacion enlistamos capas de keras hacer la fusión de tensores. Estos es, dados una lista de tensores (dos o mas) las siguientes capas generan una nueva capa. Existen distintas estrategias, como realizar una operación y regresar el resultado de dicha operación o concatenar las entradas en un tensor que agrupe a las entradas.
Suma una lista de tensores
x = keras.layers.Add()([x1, x2])
Substrae dos tensores
x = keras.layers.Substract()([x1, x2])
Conacatena una lista de tensores
x = keras.layers.Concatenate(axis=-1)([x1, x2])
Multiplica elemento-a-elemento una lista de tensores
x = keras.layers.Multiply()([x1, x2, x3])
Promedia elemento-a-elemento una lista de tensores
x = keras.layers.Averange()([x1, x2, x3])
Máximo elemento-a-elemento una lista de tensores
x = keras.layers.Maximum()([x1, x2, x3])
Mínimo elemento-a-elemento una lista de tensores
x = keras.layers.Minimum()([x1, x2, x3])
Producto punto de dos tensores
x = keras.layers.Dot()([x1, x2])
Todas las Layer arriba enlistadas tienen su respectiva interfaz funcional de la forma:
keras.layers.add(inputs)
Note que el nombre de la función empieza con minúscula y la de la Capa (Layer) con mayúscula.
Red con múltiples entradas
Un requerimiento común en las NN es la necesidad de usar múltiples entradas. Por ejemplo, en dar dos imágenes de la BD MNIST y descidir si ambas pertenecen al mísmo dígito, un par de imágenes correspondientes a frames de un video y determinar si pertenecen a la misma escena, calcular la diferencia aritmética entre dos dígtios manuscritos. Pero no estamos limitados a que las entradas sean del mismo tipo: una puede ser una imágen y la segunda una descripción de la tarea a realizar (como en un detector diseñado para buscar una clase en particular que se indica en una segunda entrada).
import keras
from keras.layers import Input, Dense
from keras.models import Model
# Dos entradas
input1 = Input(shape=(784,))
input2 = Input(shape=(784,))
# Capa que une multiples canales de procesamiento
x = keras.layers.Add()([input1, input2])
# Red Clasificadora en 10 clases
x = Dense(64, activation='relu')(x)
x = Dense(64, activation='relu')(x)
predictions = Dense(10, activation='softmax')(x)
model_multipleIn = Model(inputs=[input1, input2],
outputs=predictions)
model_multipleIn.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
# Visualización
from keras.utils import plot_model
plot_model(model_multipleIn, to_file='model_multipleIn.png',show_shapes=True, show_layer_names=True)
model_multipleIn.summary()
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_8 (InputLayer) (None, 784) 0
__________________________________________________________________________________________________
input_9 (InputLayer) (None, 784) 0
__________________________________________________________________________________________________
add_1 (Add) (None, 784) 0 input_8[0][0]
input_9[0][0]
__________________________________________________________________________________________________
dense_35 (Dense) (None, 64) 50240 add_1[0][0]
__________________________________________________________________________________________________
dense_36 (Dense) (None, 64) 4160 dense_35[0][0]
__________________________________________________________________________________________________
dense_37 (Dense) (None, 10) 650 dense_36[0][0]
==================================================================================================
Total params: 55,050
Trainable params: 55,050
Non-trainable params: 0
__________________________________________________________________________________________________
La gráfica de la NN generada com plot_model se muestra a continuación.
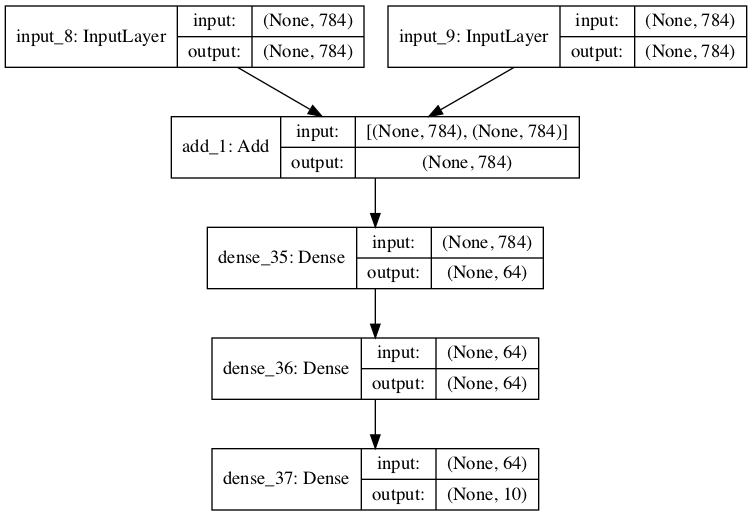
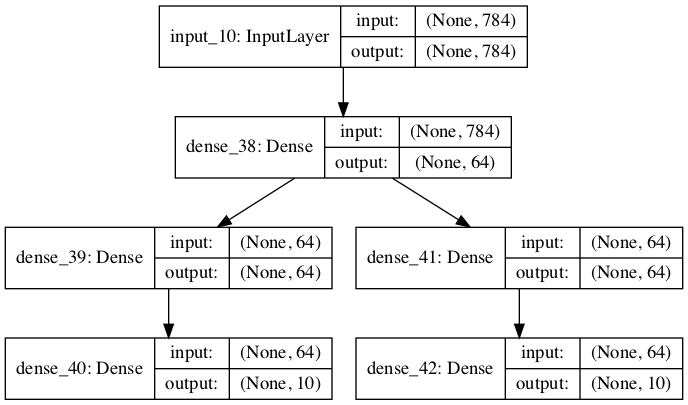
Redes con múltiples salidas
Otro caso de redes distinto a las de una-estrada/una-salida es aquella en que se requieren múltiplies salidas. Un ejemplo de ello es un analizador de imágenes médicas donde edamás de hacer detección de posibles tumores (segmentación) se desea contar con ena evaluación del mismo. O un detector de objetos que regresa: coordenadas del rectángulo que contienen algo interesante, y la probabilidad de que sea alguna de las clases de interés.
import keras
from keras.layers import Input, Dense
from keras.models import Model
# Dos entradas
input1 = Input(shape=(784,))
# Capa densa común
x = Dense(64, activation='relu')(input1)
# dos caminos de procesamiento
x2 = Dense(64, activation='relu')(x)
predictions1 = Dense(10, activation='softmax')(x2)
x3 = Dense(64, activation='relu')(x)
predictions2 = Dense(10, activation='softmax')(x3)
model_multipleOut = Model(inputs=[input1],
outputs=[predictions1, predictions2],
name='multiOut')
model_multipleOut.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
# Visualización
from keras.utils import plot_model
plot_model(model_multipleOut, to_file='model_multipleOut.png',show_shapes=True, show_layer_names=True)
model_multipleOut.summary()
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_10 (InputLayer) (None, 784) 0
__________________________________________________________________________________________________
dense_38 (Dense) (None, 64) 50240 input_10[0][0]
__________________________________________________________________________________________________
dense_39 (Dense) (None, 64) 4160 dense_38[0][0]
__________________________________________________________________________________________________
dense_41 (Dense) (None, 64) 4160 dense_38[0][0]
__________________________________________________________________________________________________
dense_40 (Dense) (None, 10) 650 dense_39[0][0]
__________________________________________________________________________________________________
dense_42 (Dense) (None, 10) 650 dense_41[0][0]
==================================================================================================
Total params: 59,860
Trainable params: 59,860
Non-trainable params: 0
__________________________________________________________________________________________________
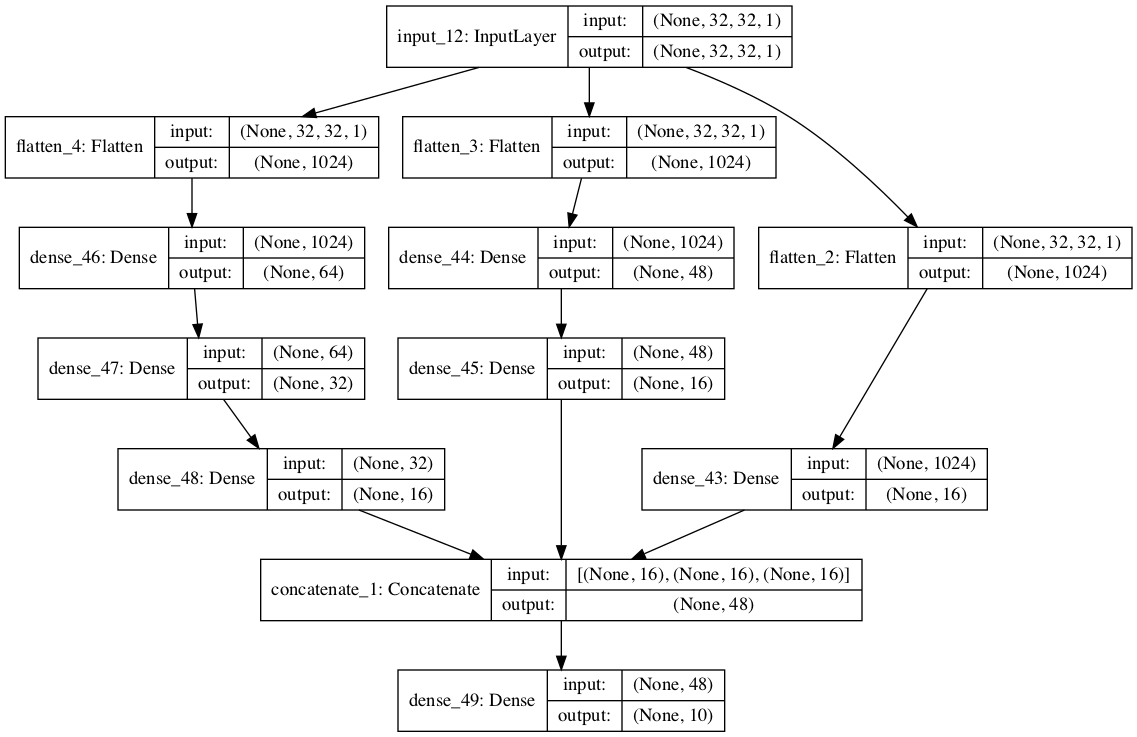
Redes con múltiples ramas
El otra característica de las NN es que pueden combinarse para desarrollar mejores clasificadores. Si asumimos el caso de reconocimiento de dígitos manuscritos mediante dos redes que hemos analizados:
-
NN Densa
-
NN Convolucional
vemos que en general la convolucional se comporta mejor que la Densa (anque en el caso de la base de datos MNIST es marginal). Lo que si es interresante de notar es que las redes tienene desempeño diferentes entre los dígitos: mientras la convolucional erró mas en distingir entre 4’s 9’s, la Densa tuvo en ese caso un mejor desempeño. Ambas redes son clasificadores que usan la información de entrada de distinta manera; en una, es importante la relación espacial de los valores analizados, mientras al otra no considera dicha información en lo absoluto. Por lo que es posible construir un clasificador que tome lo mejor de ambas si usamos una entrada (la imagen del dígito) y procedemos mediante ramas independientes a procesar: una red convolucional en una rama y una densa en la otra. Luego, antes de aplicar la discriminación, concatenamos los respuestas de las ramas y se procesas por una capa clasificadora común. Otro ejemplo es usar de redes de distinta complejidad en paralelo para completar una tarea.
img_dim = (32, 32, 1,)
img_size = img_dim[0]*img_dim[1]
num_filters = [64,32,16]
kernel_size = 3
import keras
from keras.layers import Input, Dense, Reshape, Flatten, Conv2D, LeakyReLU
from keras.models import Model
from keras import backend as K
# Dos entradas
input1 = Input(shape=img_dim)
# Rama Convolucional de procesamiento
'''
x1 = inputs
for numf in num_filters:
x1 = Conv2D(filters = numf,
kernel_size = kernel_size,
strides = 2,
padding = 'same',
activation='relu')(x1)
shape_before_flattening_x = K.int_shape(x1)
x1=Flatten()(x1)
x1out = Dense(units=16, activation='relu')(x1)
'''
# Rama 2 Densa de procesamiento
x1 = Flatten()(input1)
x1out = Dense(units=16, activation='relu')(x1)
shape_x1out = K.int_shape(x1out)
# Rama 2 Densa de procesamiento
x2 = Flatten()(input1)
x2 = Dense(units=48, activation='relu')(x2)
x2out = Dense(units=16, activation='relu')(x2)
shape_x2out = K.int_shape(x2out)
# Rama 2 Densa de procesamiento
x3 = Flatten()(input1)
x3 = Dense(units=64, activation='relu')(x3)
x3 = Dense(units=32, activation='relu')(x3)
x3out = Dense(units=16, activation='relu')(x3)
shape_x2out = K.int_shape(x3out)
# capa de union de ramas de procesamiento
x12 = keras.layers.Concatenate()([x1out, x2out, x3out])
y = Dense(10, activation='softmax')(x12)
model_multipleBranch = Model(inputs=[input1],
outputs=[y],
name='multiOut')
model_multipleBranch.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
# Visualización
from keras.utils import plot_model
plot_model(model_multipleBranch, to_file='model_multipleBranch.png',show_shapes=True, show_layer_names=True)
model_multipleBranch.summary()
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_12 (InputLayer) (None, 32, 32, 1) 0
__________________________________________________________________________________________________
flatten_4 (Flatten) (None, 1024) 0 input_12[0][0]
__________________________________________________________________________________________________
flatten_3 (Flatten) (None, 1024) 0 input_12[0][0]
__________________________________________________________________________________________________
dense_46 (Dense) (None, 64) 65600 flatten_4[0][0]
__________________________________________________________________________________________________
flatten_2 (Flatten) (None, 1024) 0 input_12[0][0]
__________________________________________________________________________________________________
dense_44 (Dense) (None, 48) 49200 flatten_3[0][0]
__________________________________________________________________________________________________
dense_47 (Dense) (None, 32) 2080 dense_46[0][0]
__________________________________________________________________________________________________
dense_43 (Dense) (None, 16) 16400 flatten_2[0][0]
__________________________________________________________________________________________________
dense_45 (Dense) (None, 16) 784 dense_44[0][0]
__________________________________________________________________________________________________
dense_48 (Dense) (None, 16) 528 dense_47[0][0]
__________________________________________________________________________________________________
concatenate_1 (Concatenate) (None, 48) 0 dense_43[0][0]
dense_45[0][0]
dense_48[0][0]
__________________________________________________________________________________________________
dense_49 (Dense) (None, 10) 490 concatenate_1[0][0]
==================================================================================================
Total params: 135,082
Trainable params: 135,082
Non-trainable params: 0
__________________________________________________________________________________________________