Introducción a Redes Neuronales Recurrentes (RNN)

Mariano Rivera

Noviembre 2018

Basado en el Cápítulo 6, Sección de Deep Learning with Python.

import keras
keras.__version__

Using TensorFlow backend.





'2.2.4'

Redes Neuronales Recurrentes

Cuando usamos una red convolucional como las de las secciones pasadas, la respuesta de la red es de esperarse que sea independiente de los datos que ha evaluado anteriormente. Es decir, no se espera que tenga memoria de lo que ha procesado y su respuesta no debe depender de los datos procesados anteriormente. La idea de las RRN es hacer uso de informacion secuencial. Esto es, para procesar datos en los cuales hay una dependencia de los datos procesados anteriormente; por ejemplo, en la predicción de series de tiempo como predecir el precio de una acción dada la información actual y los precios recientes del dicha acción.

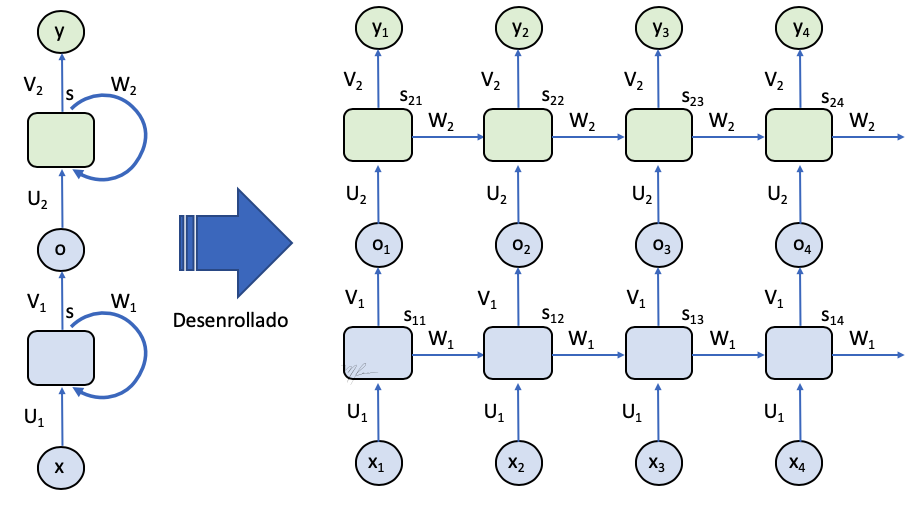
El siguiente diagrama muestra esquemas de una red secuancial y una recurrente.

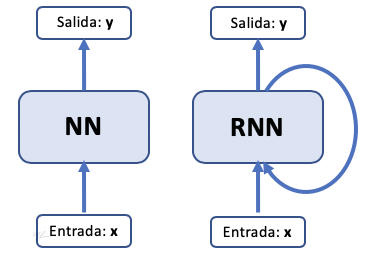
secnn_rnn

En este caso, la salida dependerá de los datos actuales y de los datos procesados anteriormente y de los cálculos realizados.

En la siguiente figura de esquematiza una red recurrente en la que se regresa todas las salidas de la secuencia procesada: desde $o_1$ hasta $o_n$ .

rnn

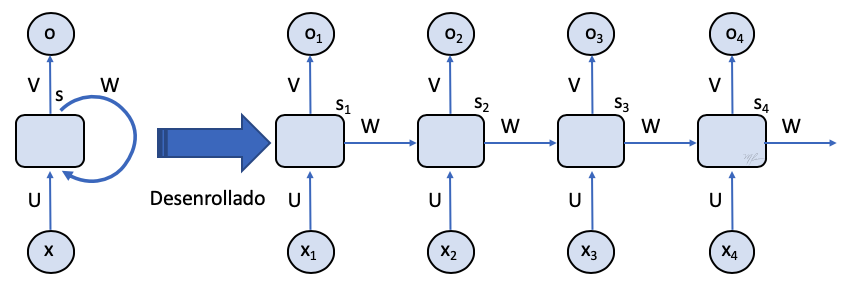
El diagrama de la izquierda muestra a una red recurrente, dicho diagrama puede desenrrollarse en el tiempo y verse como una red no recurrente. El diagrama desenrrollado de una RNN se extenderá tanto como el número de datos en el vector $x$ . En este diagrama desenrrollado puede verse que dada

$x_t$ es la entrada a tiempo $t$ .
$s_t$ es un estado oculto (interno, se denomina oculto porque no es observado ni como dato, ni como salida) a tiempo $t$ que se calcula mediante

(1)
$s_t = \phi_1(U\, x_t + W\, s_{t-1})$
donde $\phi_1$ es una función de activación

$o_t$ es la salida a tiempo $t$ que se calcula con

(2)
$o_t = \phi_2(V\, s_{t})$
donde $\phi_1$ es una función de activación

El estado oculto $s_t$ es la memoria de la red: la información que del proceso del dato actual se transmite para procesar el nuevo dato.

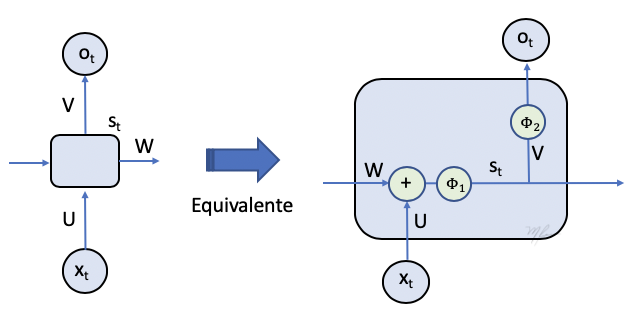
Note que ahora, la red es definida por una sola unidad, celda o cell cuyo procesamiento implica a tres matrices de pesos: $U, V$ y $W$ .

La siguiente figura ilustra los cálculos realizados por una unidad o celda de RNN.

rnn2

La clase layer de redes RNN

from keras.layers import SimpleRNN

Como cualquier otra layer de Keras, SimpleRNN procesa lotes de secuencias Numpy.

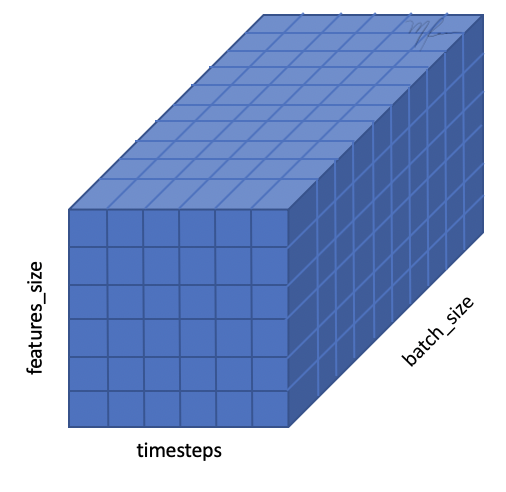
La entrada es de la forma (batch_size, timesteps, input_features)

En vez de (timesteps, input_features).

Los elementos del tensor 3D de entrada se ilustran en la siguiente figura.

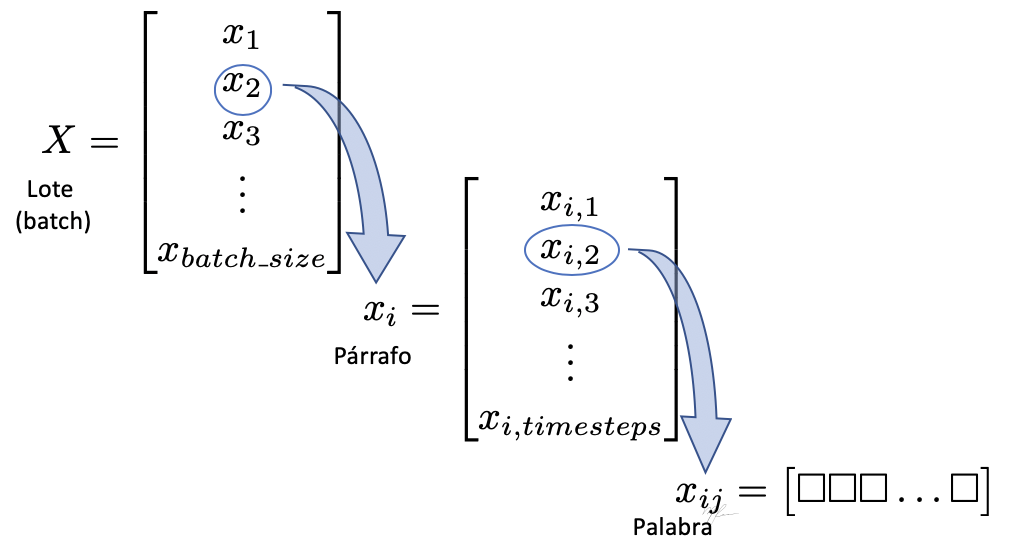
tensor3Da

El lote se compone de párrafos, que a su vez se componen de palabras que han sido encajadas (embedded) en el espacio vectorial de dimensión input_features. El tensor 3D se ilustra en la siguiente figura

tensor3Da

keras.layers.RNN(cell, 
                  return_sequences=False, 
                  return_state=False,  
                  go_backwards=False, 
                  stateful=False, 
                  unroll=False)```

**cell** es una instancia de la clase celda RNN con 

* Un método `call(input_at_t, states_at_t)`  que regresa `(output_at_t, states_at_t_plus_1)`. El método `cell` puede tomar argumentos constantes adicionales.

* Atributo `state_size` entero que indica el tamaño del estado recurrente ($s$), de la misma dimensión que la salida $o$. Una dimensión por estado (pueded ser lista/tupla de enteros).

* Atributo `output_size` . Puede ser un entero o tensor representando la forma de la salida. Si no se define, se infiere de  `state_size`

**return_sequences y return_state**

La salida se controla mediante argumentos del constructor 

Si `return_state==True` : se regresa una lista de tensores de la forma (batch_size, units). El primer tensor es la salida y los restantes son los último estados.

Si `return_sequence==True`: se regresa un tensor 3D con forma (batch_size, timesteps, units). en otro caso un tensor 2Dcon forma (batch_size, units).

**go_backwards**: Si es `True`, se procesa la secuencia de entrada en orden inverso (de atrás hacia adelante) 

**stateful**:  Si es `True`,  el último estado de la muetsra de un lote es usado para continuar el procesamiento del siguiente lote. 

**unroll**:  Si es `True`, la red será desenrollada, en otro caso se usa un loop simbólico. Desenrollar una RNN pueded acelerar el procesamiento, es adecuado para secuencias cortas. 


**input_dim**: dimensión de la entrada (input_shape) is requerido si se usa un *layer* RNN como primera capa de un modelo

**input_length**: longitud de la secuencia de entrada. Requerido se si conecta a una *layer* *Flatten*. Permite calcular la dimensión de la salida.

### RNN que regresa únicamente la última salida de cada secuencia de entrada

Tensor 2D tensor de forma `(batch_size, output_features)`)



```python
from keras.models import Sequential
from keras.layers import Embedding, SimpleRNN

model = Sequential()

Se usa un embedding con tamaño de diccionario a los más de 10,000 y se mapean a dimensión un vector de dimensión 32.

model.add(Embedding(10000, 32))  
model.add(SimpleRNN(32))

Resumen de la arquitectura

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_1 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, 32)                2080      
=================================================================
Total params: 322,080
Trainable params: 322,080
Non-trainable params: 0
_________________________________________________________________

RNN que regresa la secuencia de salida completa para cada secuencia procesada

Tensor 3D de forma (batch_size, timesteps, output_features))

note el parámetro en
model.add(SimpleRNN(32, return_sequences=True))

model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_2 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_2 (SimpleRNN)     (None, None, 32)          2080      
=================================================================
Total params: 322,080
Trainable params: 322,080
Non-trainable params: 0
_________________________________________________________________

RNNs apiladas (Stack)

Esto nos permite incrementar la capacidad de a red

Es necesario que todas las capas intermedias regresan las secuencias completas

Excepto la última capa que, en este caso, regresa sólo la última salida de la secuencia procesada.

El siguiente diagrama ilustra capas RNN apiladas (stacked) en la que se regresa todas las salidas de la secuencia procesada: desde $y_1$ hasta $y_n$ .

rnn_stack

model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32))  # Salida de la ultima capa, solo de última celda
model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_3 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_3 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_4 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_5 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_6 (SimpleRNN)     (None, 32)                2080      
=================================================================
Total params: 328,320
Trainable params: 328,320
Non-trainable params: 0
_________________________________________________________________

Ejemplo con BD de clasificación de comentarios de películas

Pre-procesamiento de los datos

from keras.datasets import imdb
from keras.preprocessing import sequence

max_features = 10000  # tamaño del diccionario de palabras comunes
                      # (número de palabras a utilizar)
maxlen = 500          # longitud máxima de cada secuencia 
batch_size = 32

print('Cargando Datos...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
print(len(input_train), 'Secuencia de entrenamiento')
print(len(input_test),  'Secuencia de prueba')

#input_train[:] = (input_train[:])[-1::-1]

Cargando Datos...
25000 Secuencia de entrenamiento
25000 Secuencia de prueba

print('*Pad* de las secuencias (muestras x longitud)')
input_train = sequence.pad_sequences(input_train, maxlen=maxlen)
input_test = sequence.pad_sequences(input_test, maxlen=maxlen)
print('Forma de input_train:', input_train.shape)
print('Forma de input_test:', input_test.shape)

*Pad* de las secuencias (muestras x longitud)
Forma de input_train: (25000, 500)
Forma de input_test: (25000, 500)

RNN con una capa Embedding y una capa SimpleRNN que regresa solo una salida para cada secuencia

from keras.layers import Dense

model = Sequential()
# Capa embedding
# input_dim : tamaño del vocabulario
# output_dim: dimensión del vector al que se mapea
model.add(Embedding(input_dim=max_features, output_dim=32))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_4 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_7 (SimpleRNN)     (None, 32)                2080      
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 33        
=================================================================
Total params: 322,113
Trainable params: 322,113
Non-trainable params: 0
_________________________________________________________________

model.compile(optimizer='rmsprop', 
              loss='binary_crossentropy',
              metrics=['acc'])

import time
tic = time.time()
history = model.fit(input_train, y_train,
                    epochs=10,
                    batch_size=128,
                    validation_split=0.2,
                    verbose=2)
print('Tiempo de entrenamiento:', time.time()-tic)

Train on 20000 samples, validate on 5000 samples
Epoch 1/10
 - 27s - loss: 0.6433 - acc: 0.6143 - val_loss: 0.5097 - val_acc: 0.7864
Epoch 2/10
 - 21s - loss: 0.4190 - acc: 0.8211 - val_loss: 0.4309 - val_acc: 0.8060
Epoch 3/10
 - 21s - loss: 0.3121 - acc: 0.8763 - val_loss: 0.3700 - val_acc: 0.8436
Epoch 4/10
 - 21s - loss: 0.2585 - acc: 0.9005 - val_loss: 0.3432 - val_acc: 0.8690
Epoch 5/10
 - 20s - loss: 0.2094 - acc: 0.9220 - val_loss: 0.3670 - val_acc: 0.8514
Epoch 6/10
 - 20s - loss: 0.1664 - acc: 0.9403 - val_loss: 0.3700 - val_acc: 0.8686
Epoch 7/10
 - 20s - loss: 0.1340 - acc: 0.9519 - val_loss: 0.3785 - val_acc: 0.8624
Epoch 8/10
 - 20s - loss: 0.0874 - acc: 0.9695 - val_loss: 0.4734 - val_acc: 0.8066
Epoch 9/10
 - 20s - loss: 0.0569 - acc: 0.9827 - val_loss: 0.6423 - val_acc: 0.7984
Epoch 10/10
 - 19s - loss: 0.0419 - acc: 0.9879 - val_loss: 0.5613 - val_acc: 0.8158
Tiempo de entrenamiento: 208.5378966331482

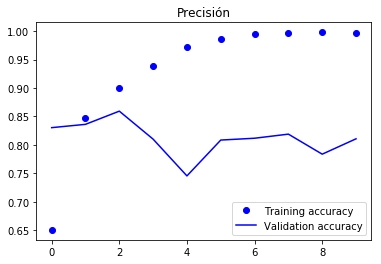
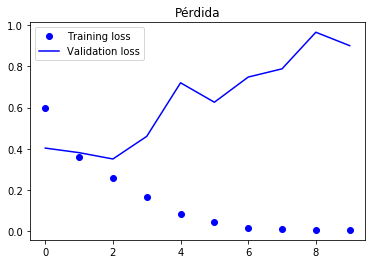
Gráficas del función de pérdida y de la precisión

import matplotlib.pyplot as plt

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(len(acc))

plt.plot(epochs, acc, 'bo', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Precisión')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Pérdida')
plt.legend()

plt.show()

<Figure size 640x480 with 1 Axes>



<Figure size 640x480 with 1 Axes>

Llegamos alrededor de 85% de precisión en el conjunto de validación, una red densa simple llegó al 88%.

Parte del problema es que sólo consideramos las primeras 500 palabras, que son menos que la que accesaba la red original.

Ejemplo con Stack de RNNs

from keras.layers import Dense

model = Sequential()
# Capa embedding
# input_dim : tamaño del vocabulario
# output_dim: dimensión del vector al que se mapea
model.add(Embedding(input_dim=max_features, output_dim=32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))

model.summary()

model.compile(optimizer='rmsprop', 
              loss='binary_crossentropy',
              metrics=['acc'])

import time
tic = time.time()
history_stackRNN = model.fit(input_train, y_train,
                    epochs=10,
                    batch_size=128,
                    validation_split=0.2,
                    verbose=2)
print('Tiempo de entrenamiento:', time.time()-tic)

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_5 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_8 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_9 (SimpleRNN)     (None, 32)                2080      
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 33        
=================================================================
Total params: 324,193
Trainable params: 324,193
Non-trainable params: 0
_________________________________________________________________
Train on 20000 samples, validate on 5000 samples
Epoch 1/10
 - 38s - loss: 0.5967 - acc: 0.6507 - val_loss: 0.4037 - val_acc: 0.8304
Epoch 2/10
 - 37s - loss: 0.3586 - acc: 0.8479 - val_loss: 0.3816 - val_acc: 0.8362
Epoch 3/10
 - 38s - loss: 0.2585 - acc: 0.8999 - val_loss: 0.3509 - val_acc: 0.8594
Epoch 4/10
 - 36s - loss: 0.1652 - acc: 0.9387 - val_loss: 0.4606 - val_acc: 0.8102
Epoch 5/10
 - 37s - loss: 0.0857 - acc: 0.9714 - val_loss: 0.7201 - val_acc: 0.7456
Epoch 6/10
 - 35s - loss: 0.0444 - acc: 0.9856 - val_loss: 0.6260 - val_acc: 0.8086
Epoch 7/10
 - 36s - loss: 0.0187 - acc: 0.9945 - val_loss: 0.7478 - val_acc: 0.8118
Epoch 8/10
 - 35s - loss: 0.0106 - acc: 0.9965 - val_loss: 0.7877 - val_acc: 0.8190
Epoch 9/10
 - 36s - loss: 0.0073 - acc: 0.9981 - val_loss: 0.9650 - val_acc: 0.7838
Epoch 10/10
 - 36s - loss: 0.0084 - acc: 0.9976 - val_loss: 0.9000 - val_acc: 0.8108
Tiempo de entrenamiento: 364.4030888080597

El tiempo por época es prácticamente el doble, 26 secs por época en TitanXP y 36 p/época en GTX20180.

Pero no mejora el desempeño, precisión de validación de cerca de 86% en la segunda época.

Apilando 3 RNNs, seguimos en el 85% de precisión en el conjunto de validación. 37 secs. por época en Titan XP

import matplotlib.pyplot as plt

acc = history_stackRNN.history['acc']
val_acc = history_stackRNN.history['val_acc']
loss = history_stackRNN.history['loss']
val_loss = history_stackRNN.history['val_loss']

epochs = range(len(acc))

plt.plot(epochs, acc, 'bo', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Precisión')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Pérdida')
plt.legend()

plt.show()

png

Alargar las secuencias no mejora con la RNN, pues no son buenas para recordar términos cortos por mucho tiempo. Tampoco el apilar agregar RNNs. Veamos una red especialista en estos casos

Red de Memoria Corta a Largo Plazo (Long-Term Short Memory, LTSM)

[2]_ S. Hochreiter and J. Schimidhuber, Longe short-term memory, Neural Computation, 9(8), 1735-1780, 1997.

Similarmente a la SimpleRNN que recién vimos, usamos los defaults y vemos como se comporta.

La celda de la LTSM se ilustra a continuación

lstm

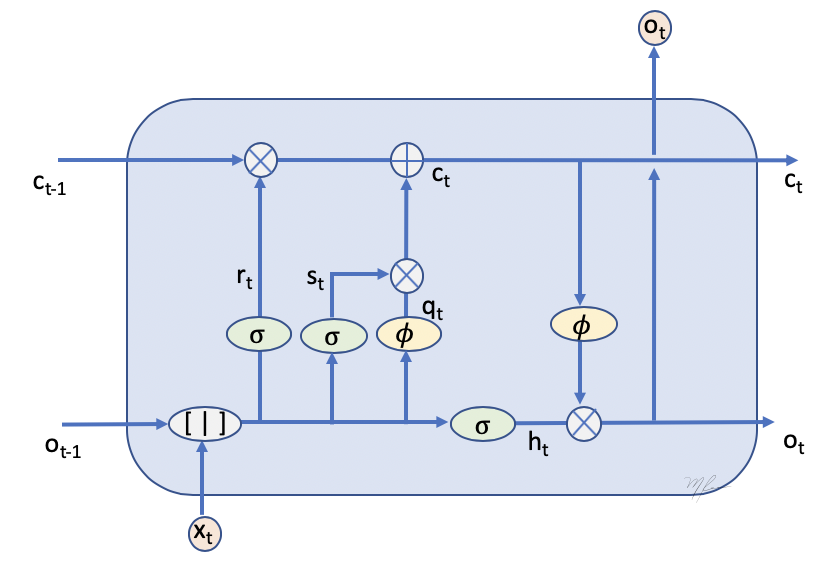
En esta ilustración, notamos las siguientes variables:

$x_t$ es la entrada en el tiempo $t$ .
$o_{t-1}$ es la salida de la celda en tiempo $t-1$ , la salida anterior.
$c_{t-1}$ es la información (memoria) que es pasada por la estapa anterior.
$c_{t}$ es la informacion que es pasada a la sigiente etapa.

Luego, la celda tienen tres entradas $[x_t , o_{t-1}, c_{t-1}]$ y tres salidas $[o_t, c_t]$ .

Las $\phi$ 's denotan funciones de activación, generalmente tangente hiperbólicas.
La operación $[\; | \;]$ denota concatenación de las entradas.
El operador $\oplus$ denota suma de tensores.
Las funciones $\sigma$ son sigmoides que aproximan a una respuesta binaria, $\{0,1\}$ . Su operación en combinación con el producto $\otimes$ pueden entenderse como switches que permiten el flujo, o no, de la información. Ver la siguiente figura.

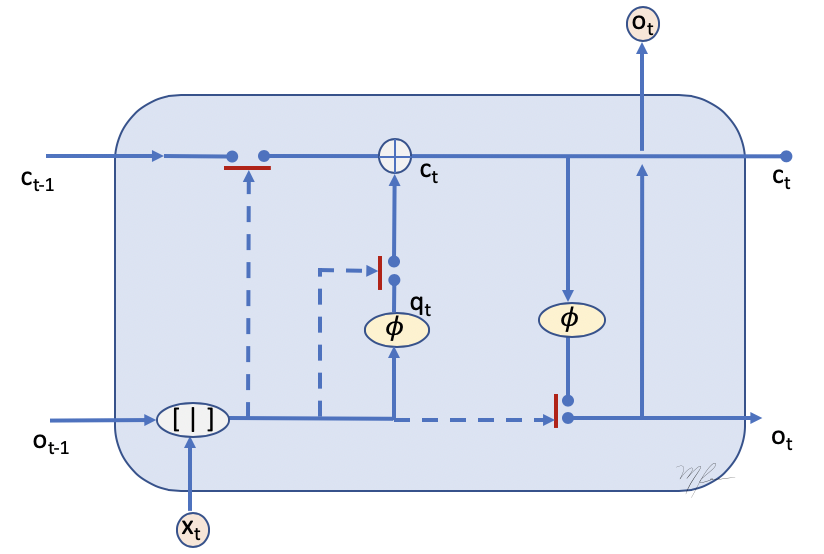
lstm_switch

Canal de memoria

La memoria de término largo permite que la información pase desde $c_{t-1}$ a $c_t$ .

Luego la memoria se obtienen como la suma de información de en la memoria $c_{t-1}$ que deseamos preservar y la información nueva $q_t$ que deseamos agregar al la memoria:

(3)
$c_t = r_t * c_{t-1} + s_t * q_t$
donde la información $q_t$ a agredar se obtiene a partir de procesar la entrada y la salida anterior:

(4)
$q_t = \phi(W_q [x_t | o_{t-q}] + b_q)$
donde $r_t$ y $s_t$ son switches que controlan el “olvido” de la memoria pasada y la nueva información nueva a “recordar”.

Dependiendo de los datos $x_t$ y de la salida anterior $o_{t-1}$ , la celda “olvidará” lo que el canal de memoria ha conservado .

El switch de “reseteo” de memoria se calcula mediante:

(5)
$r_t = \sigma(W_r [x_t | o_{t-q}] + b_r)$
donde el $b_r$ representa el bias.

El switch para agregar información a la memoria se calcula mediante:

(6)
$s_t = \sigma(W_s [x_t | o_{t-1}] + b_s)$
donde el $b_s$ representa el bias.

Canal de salida

La célula dará como salida una selección del resultado de procesar el contenido actualizado de la memoria.

(7)
$o_t = h_t * \phi ( W_o \, c_t + b_o)$

donde el switch de selección se calula usando

(8)
$h_t = \sigma(W_h [x_t | o_{t-1}] + b_h)$
donde el $b_h$ representa el bias.

Para mas información en el tema, ver Ref [2] y el blog de Colah, donde se disculten otras variantes.

La capa LSTM de KERAS

keras.layers.LSTM(units, 
                  activation='tanh', 
                  recurrent_activation='hard_sigmoid', 
                  use_bias=True, 
                  kernel_initializer='glorot_uniform', 
                  recurrent_initializer='orthogonal', 
                  bias_initializer='zeros', 
                  unit_forget_bias=True, 
                  kernel_regularizer=None, 
                  recurrent_regularizer=None, 
                  bias_regularizer=None, 
                  activity_regularizer=None, 
                  kernel_constraint=None, 
                  recurrent_constraint=None, 
                  bias_constraint=None, 
                  dropout=0.0, 
                  recurrent_dropout=0.0, 
                  implementation=1, 
                  return_sequences=False, 
                  return_state=False, 
                  go_backwards=False, 
                  stateful=False, 
                  unroll=False)```


En el caso de Keras, la implementación de la LSTM esta dada por


**Salida**

La salida de la celda con:

(11)
$$
o_t = \phi( W_{x} x_t + W_{o} o_{t-1} + W_c c_{t-1} + b_o)
$$

que incluye el efecto de los datos $x_t$, el el estado anterior (salida) $o_{t-1}$ y la memoria acumulada $c_{t-1}$


**Canal de Memoria**

Y el canal de memoria se actualiza similarmente como en (3):

(9)
$$
 c_t =  r_t * c_{t-1} + s_t * q_t
$$

La diferencia mayor esta en que los demás componentes se calculan con

(10)
$$
r_t = \phi( W_{rx} x_t + W_{ro} o_{t-1} + b_r) \\
s_t = \phi( W_{sx} x_t + W_{so} o_{t-1} + b_s) \\
q_t = \phi( W_{qx} x_t + W_{qx} o_{t-1} + b_q) 
$$

Note que se usa una sola funcion de activación, 




```python
from keras.layers import LSTM

print('Número máximo de palabras a usar:', max_features)

Número máximo de palabras a usar: 10000

Creamos el modelo con la incrustación (embedding)

model = Sequential()
model.add(Embedding(max_features, 32))

Incluimos una capa LSTM

model.add(LSTM(32))
model.add(Dense(1, activation='sigmoid'))

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_5 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
lstm_6 (LSTM)                (None, 32)                8320      
_________________________________________________________________
dense_4 (Dense)              (None, 1)                 33        
=================================================================
Total params: 328,353
Trainable params: 328,353
Non-trainable params: 0
_________________________________________________________________

Parámetros de entrenamiento

model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['acc'])

y entrenamos

tic=time.time()
history = model.fit(input_train, y_train,
                    epochs=6,
                    batch_size=128,
                    validation_split=0.2,
                    verbose=2)
print('tiempo de entrenamiento: ', time.time()-tic)

Train on 20000 samples, validate on 5000 samples
Epoch 1/6
 - 60s - loss: 0.5069 - acc: 0.7563 - val_loss: 0.3252 - val_acc: 0.8670
Epoch 2/6
 - 62s - loss: 0.2893 - acc: 0.8846 - val_loss: 0.3436 - val_acc: 0.8488
Epoch 3/6
 - 62s - loss: 0.2325 - acc: 0.9115 - val_loss: 0.3455 - val_acc: 0.8598
Epoch 4/6
 - 64s - loss: 0.2013 - acc: 0.9253 - val_loss: 0.3966 - val_acc: 0.8636
Epoch 5/6
 - 64s - loss: 0.1778 - acc: 0.9368 - val_loss: 0.3590 - val_acc: 0.8402
Epoch 6/6
 - 64s - loss: 0.1643 - acc: 0.9426 - val_loss: 0.3489 - val_acc: 0.8700
tiempo de entrenamiento:  375.3736391067505

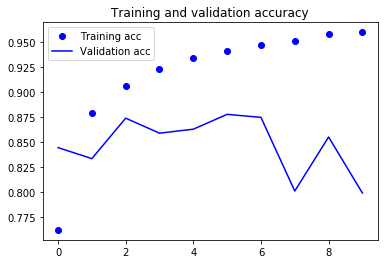
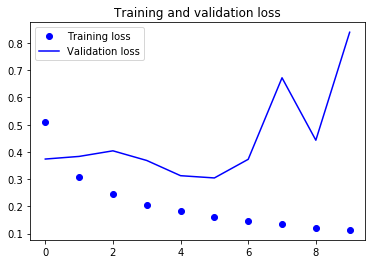
Gráficas del función de pérdida y de la precisión

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(len(acc))

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.show()

png

import numpy as np

print('La precisión alcanza un {}%'.format(np.array(val_acc).max()*100))

La precisión alcanza un 87.8%

Redes con Unidades Recurrentes con Compuertas (Gated-RU)

[3] K. Kyunghyun et al. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation, Proc EMNLP, 1724-1734 (2014)

Otro tipo de redes recurrentes inspripadas en las LSTM son las Redes Recurrentes con Conpuertas (Gated Recurrent Neuranl Networks, GRU). Dichas redes mejoran la memoria de largo tiempo a un costo computacional menor que las LSTM a costa de un menor desempeño. Son un punto medio entre las RRN y las LSTM. Su simpleza permite que sean ampliamente usadas, dado que son mas fáciles de entrenar y son más rápidas en la inferencia que las LSTM. Estas redes fueron propuestas en [3] para realizar la tarea de traducir del inglés al francés. El modelo es entrenado para aprender la probabilidad de traducción de una frase en inglés a una frase en francés.

La notación de las GRN es:

$x_t$ : dato en tiempo actual (entrada)
$o_t$ : salida en tiempo actual
$o_{t-1}$ : salida en el tiempo previo (memoria)

En estas redes, la salida y la memoria van por el mismo conducto, se puede ver a $o$ como la estimación actual de la red dada la información al momento disponible.

Exiten dos switches (gates) denominados:

Switch de “reset”, que hace a la unidad olvidar lo acumulado en memoria para calcular su nueva salida:

(11)
$r_t = \sigma(W_{rx} x_t + W_{ro} o_{t-1} +b_z)$

Switch de actualización, que hace que la solcuión acumulada sea actualizada o se usa la solución anterior como solución de la unidad actual. Es es útil para los casos en que la información actual no aporta información relevante.

(11)
$z_t = \sigma(W_{zx} x_t + W_{zo} o_{t-1} +b_z)$

La salida de la red se selecciona con $z$ mediante

(12)
$o_t = z_t o_{t-1} + (1-z_t) \tilde o_t$

donde $\tilde o_t$ es la respuesta de la red dada la información disponible: $x_t$ y $o_{t-1}$ . Se calcula mendiante

(12)
$\tilde o_t = \phi(W x_t + r_t \odot \tilde o_{t-1})$

donde $\odot$ representa el producto punto a punto, aquiíes donde se olvida o no la información en la memoria.

Gráficamente la GRU se ilustra en la siguiente figura

GRU1

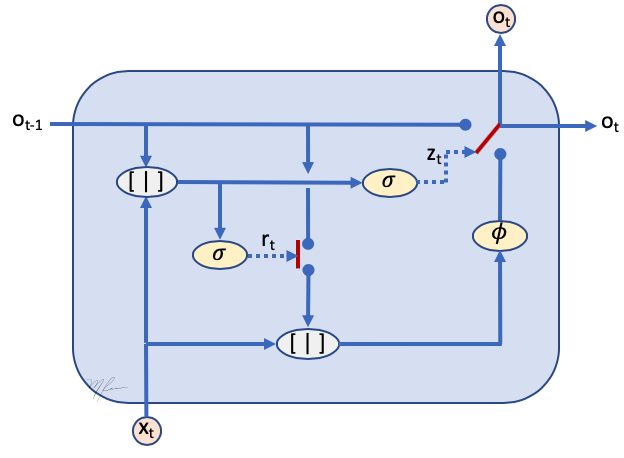
Es más claro si analizamos sólo la construcción de la salida, e indicamos los switches (los cuales se aprenden a partir de la información accesible a la unidad), vea la siguiente figura.

GRU2

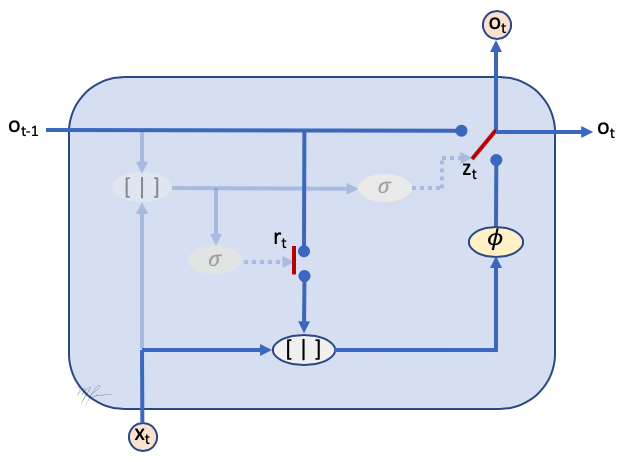
De esta figura vemos que

Las entradas a la celda son la salida de la celda anterior y el dato actual.
La salida de la celda anterior puede o no (switch $r_t$ ) usarse para procesarse en la celda.
La celda calcula una respuesta tomando en cuenta la entrada actual y (en su caso) la memoria.
La salida de la celda se elige (switch $z_t$ ) de entre la salida anterior (memoria) o la procesada por la celda.

from keras.datasets import imdb
from keras.preprocessing import sequence

max_features = 10000  # tamaño del diccionario de palabras comunes
                      # (número de palabras a utilizar)
maxlen = 500          # longitud máxima de cada secuencia 
batch_size = 32

print('Cargando Datos...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
print(len(input_train), 'Secuencia de entrenamiento')
print(len(input_test),  'Secuencia de prueba')

print('*Pad* de las secuencias (muestras x longitud)')
input_train = sequence.pad_sequences(input_train, maxlen=maxlen)
input_test = sequence.pad_sequences(input_test, maxlen=maxlen)

Using TensorFlow backend.


Cargando Datos...
25000 Secuencia de entrenamiento
25000 Secuencia de prueba
*Pad* de las secuencias (muestras x longitud)

from keras.models import Sequential
#from keras import layers
from keras.layers import Dense, GRU, Embedding

model = Sequential()
# Capa embedding
# input_dim : tamaño del vocabulario
# output_dim: dimensión del vector al que se mapea

model.add(Embedding(input_dim=max_features, output_dim=32))
# comentar la siguiente linea para evaluar dropout 
model.add(GRU(32))
# descomentar la siguiente linea para evaluatr dropout 
#model.add(GRU(32, dropout=.2, recurrent_dropout=0.2))
model.add(Dense(1, activation='sigmoid'))

model.summary()

model.compile(optimizer='rmsprop', 
              loss='binary_crossentropy',
              metrics=['acc'])

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_6 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
gru_4 (GRU)                  (None, 32)                6240      
_________________________________________________________________
dense_5 (Dense)              (None, 1)                 33        
=================================================================
Total params: 326,273
Trainable params: 326,273
Non-trainable params: 0
_________________________________________________________________

import time
tic = time.time()
history_GRU = model.fit(input_train, y_train,
                        epochs=10,
                        batch_size=128,
                        validation_split=0.2,
                        verbose=2)
print('Tiempo de entrenamiento:', time.time()-tic)

Train on 20000 samples, validate on 5000 samples
Epoch 1/10
 - 60s - loss: 0.5872 - acc: 0.6929 - val_loss: 0.4735 - val_acc: 0.7714
Epoch 2/10
 - 57s - loss: 0.4194 - acc: 0.8173 - val_loss: 0.4220 - val_acc: 0.8114
Epoch 3/10
 - 57s - loss: 0.3638 - acc: 0.8505 - val_loss: 0.4152 - val_acc: 0.8098
Epoch 4/10
 - 57s - loss: 0.3327 - acc: 0.8659 - val_loss: 0.3698 - val_acc: 0.8498
Epoch 5/10
 - 57s - loss: 0.3083 - acc: 0.8788 - val_loss: 0.3902 - val_acc: 0.8266
Epoch 6/10
 - 58s - loss: 0.2907 - acc: 0.8870 - val_loss: 0.3946 - val_acc: 0.8366
Epoch 7/10
 - 58s - loss: 0.2745 - acc: 0.8942 - val_loss: 0.4113 - val_acc: 0.8162
Epoch 8/10
 - 58s - loss: 0.2581 - acc: 0.9037 - val_loss: 0.3947 - val_acc: 0.8298
Epoch 9/10
 - 58s - loss: 0.2396 - acc: 0.9104 - val_loss: 0.3760 - val_acc: 0.8472
Epoch 10/10
 - 58s - loss: 0.2259 - acc: 0.9143 - val_loss: 0.4318 - val_acc: 0.8166
Tiempo de entrenamiento: 579.4633202552795

SIN DROPOUT: Logramos en mejor desempeño de 87.44%, muy cercano a la LSTM de 87.6%, con una red mas simple.

CON DROPOUT: No hay mejora, de hecho alcanza una precisión del 95%, por debajo del mismo modelo si no usamos doropout. Para este caso, el sobreajuste no es el principal problema, debe ser el tamaño de la DB, la cual es relativamente pequeña.

Redes Recurrentes Bidireccionales (B-RNN)

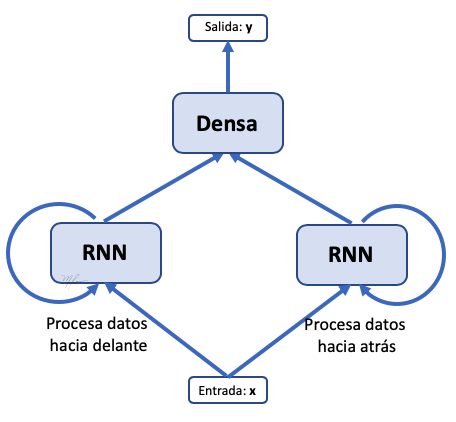
rnn_bidireccional

Keras provee una celda que ya combina las dos redes recurrentes (la que procesa en orden hacia delante y la que procesa en order inverso) y que integra en una sola salida ambas respuestas, la forma de crear una RNN (LSTM en este caso) bidireccional en Keras se detalla en seguida.

from keras.datasets import imdb
from keras.preprocessing import sequence

max_features = 10000  # tamaño del diccionario de palabras comunes
                      # (número de palabras a utilizar)
maxlen = 500          # longitud máxima de cada secuencia 
batch_size = 32

print('Cargando Datos...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
print(len(input_train), 'Secuencia de entrenamiento')
print(len(input_test),  'Secuencia de prueba')

print('*Pad* de las secuencias (muestras x longitud)')
input_train = sequence.pad_sequences(input_train, maxlen=maxlen)
input_test = sequence.pad_sequences(input_test, maxlen=maxlen)

Using TensorFlow backend.


Cargando Datos...
25000 Secuencia de entrenamiento
25000 Secuencia de prueba
*Pad* de las secuencias (muestras x longitud)

from keras.models import Sequential
#from keras import layers
from keras.layers import Dense, LSTM, Bidirectional, Embedding

model = Sequential()
# Capa embedding
# input_dim : tamaño del vocabulario
# output_dim: dimensión del vector al que se mapea

model.add(Embedding(input_dim=max_features, output_dim=32))
model.add(Bidirectional(LSTM(32)))
model.add(Dense(1, activation='sigmoid'))

model.summary()

model.compile(optimizer='rmsprop', 
              loss='binary_crossentropy',
              metrics=['acc'])

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_2 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
bidirectional_2 (Bidirection (None, 64)                16640     
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 65        
=================================================================
Total params: 336,705
Trainable params: 336,705
Non-trainable params: 0
_________________________________________________________________

import time
tic = time.time()
history_STLM = model.fit(input_train, y_train,
                         epochs=10,
                         batch_size=128,
                         validation_split=0.2,
                         verbose=2)
print('Tiempo de entrenamiento:', time.time()-tic)

Train on 20000 samples, validate on 5000 samples
Epoch 1/10
 - 84s - loss: 0.5491 - acc: 0.7281 - val_loss: 0.5089 - val_acc: 0.7438
Epoch 2/10
 - 79s - loss: 0.3262 - acc: 0.8701 - val_loss: 0.3593 - val_acc: 0.8596
Epoch 3/10
 - 79s - loss: 0.2490 - acc: 0.9062 - val_loss: 0.2982 - val_acc: 0.8764
Epoch 4/10
 - 79s - loss: 0.2127 - acc: 0.9221 - val_loss: 0.3524 - val_acc: 0.8550
Epoch 5/10
 - 80s - loss: 0.1866 - acc: 0.9319 - val_loss: 0.3299 - val_acc: 0.8700
Epoch 6/10
 - 79s - loss: 0.1605 - acc: 0.9435 - val_loss: 0.3743 - val_acc: 0.8536
Epoch 7/10
 - 86s - loss: 0.1474 - acc: 0.9485 - val_loss: 0.3282 - val_acc: 0.8878
Epoch 8/10
 - 81s - loss: 0.1394 - acc: 0.9519 - val_loss: 0.3858 - val_acc: 0.8498
Epoch 9/10
 - 81s - loss: 0.1333 - acc: 0.9540 - val_loss: 0.3345 - val_acc: 0.8844
Epoch 10/10
 - 81s - loss: 0.1217 - acc: 0.9571 - val_loss: 0.3702 - val_acc: 0.8716
Tiempo de entrenamiento: 811.7054271697998

El desempeño en un poco mejor, cercano al 89%, ya supera a una red Densa que logra un desempeño del 88%.