Análsis de Componentes Principales

(Principal Component Analysis, PCA)

Mariano Rivera

Mayo 2017

PCA es un un método de transformación lineal de los datos que decorrelacional variables Gaussianas multivariadas
Inventado por el matemático-bioestadístico Pearson [1].
Es un método exploratorio que se a popularizado para reducir la dimensión de variables multivaluadas

[1 ] Pearson, K. (1901). “On Lines and Planes of Closest Fit to Systems of Points in Space,” Philosophical Magazine. 2 (11): 559–572. doi:10.1080/14786440109462720.

%matplotlib inline
#%matplotlib notebook
import numpy as np 
import sklearn as skl
import matplotlib.pyplot as plt
from PIL import Image

#---------------------------------------------------------------------
def printArray(X, precision=3, suppress = True):
    printOptionsOld = np.get_printoptions()
    np.set_printoptions(precision=precision, suppress=suppress)      
    print(X)
    np.set_printoptions(**printOptionsOld)
#---------------------------------------------------------------------

Datos Sintéticos

Para introducir el tema, generamos muestras con distribuciones Gaussianas multivariadas; i.e., cada dato en un vector.

Distribución Gaussiana multivariada decorrelacionada

El primer caso, corresponde a una Gaussiana multivariada no correlacionada con dimensión $n$ . Sea $x_i$ el $i$ -ésimo dato de la muestra con $i=1,2,\ldots, m$ . Entonces,

(1)
$x_{ij} \sim \mathcal{N}(\mu_j, \sigma_j^2)$

donde $\mu_j$ y $\sigma_j^2$ son la media y la variaza de la variable $j$ -ésima, respectivamente.

Luego la muestra esta dada por:

(2)
$X = \begin{bmatrix} x^\top_1 \\ x^\top_2 \\ \vdots \\ x^\top_m \end{bmatrix}$
con $x_i \in \mathbb{R}^n$

La covarianza entre las $n$ variables se obtienen mediante

(3)
$s^2_{jk} = \frac{1}{m-1}\sum_i (x_{ij}-\mu'_j)(x_{ik}-\mu'_k); \;\;\;\;\text{ para } \;\; j,k = 1,2,\ldots,n.$

donde $\{\mu'_j\}$ son las medias muestrales (estimación de $\{\mu_j\}$ ).

En forma matricial este cálculo se obtienen

(4)
$\Sigma = \frac{1}{m-1} X^\top X = \frac{1}{m-1} \begin{bmatrix} s_{11}^2, & s_{12}^2, & \ldots & s_{1n}^2 \\ s_{21}^2, & s_{22}^2, & \ldots & s_{2n}^2 \\ \vdots & \vdots & \ddots & \vdots \\ s_{n1}^2, & s_{n2}^2, & \ldots & s_{nn}^2 \end{bmatrix}$
con $x_i \in \mathbb{R}^n$

Operación simbólica en Python usando la librería Sympy

from sympy import *
init_printing()

# x'sa minúsculas son las entradas de la matriz de datos
# Xi mayúsculas es cada observacion
# Xses ma muestra toital (todos los datos ordenados por renglon), ecuación (2)

X1 = Matrix(symbols('x1(1:4)'))
X2 = Matrix(symbols('x2(1:4)'))
X3 = Matrix(symbols('x3(1:4)'))
X4 = Matrix(symbols('x4(1:4)'))
          
Xs = Matrix([X1.T, X2.T, X3.T, X4.T])
Xs

$\left[\begin{matrix}x_{11} & x_{12} & x_{13}\\x_{21} & x_{22} & x_{23}\\x_{31} & x_{32} & x_{33}\\x_{41} & x_{42} & x_{43}\end{matrix}\right]$

#matriz de covarianzas (escalada por m), ecuación (4)
Xs.T*Xs

$\left[\begin{matrix}x_{11}^{2} + x_{21}^{2} + x_{31}^{2} + x_{41}^{2} & x_{11} x_{12} + x_{21} x_{22} + x_{31} x_{32} + x_{41} x_{42} & x_{11} x_{13} + x_{21} x_{23} + x_{31} x_{33} + x_{41} x_{43}\\x_{11} x_{12} + x_{21} x_{22} + x_{31} x_{32} + x_{41} x_{42} & x_{12}^{2} + x_{22}^{2} + x_{32}^{2} + x_{42}^{2} & x_{12} x_{13} + x_{22} x_{23} + x_{32} x_{33} + x_{42} x_{43}\\x_{11} x_{13} + x_{21} x_{23} + x_{31} x_{33} + x_{41} x_{43} & x_{12} x_{13} + x_{22} x_{23} + x_{32} x_{33} + x_{42} x_{43} & x_{13}^{2} + x_{23}^{2} + x_{33}^{2} + x_{43}^{2}\end{matrix}\right]$

Que es lo mismo que

$X^\top X = \begin{bmatrix} x_1, x_2, \ldots, x_m \end{bmatrix} \begin{bmatrix} x^\top_1 \\ x^\top_2 \\ \vdots \\ x^\top_m \end{bmatrix} = \sum_{j=1}^m x_j x_j^\top$

# simbólicamente
(X1*X1.T+X2*X2.T+X3*X3.T+X4*X4.T)

Forma estandarizada (normalizada) $z$ de una variable aleatoria $x$

Esta forma se obtienen dividiendo cada variable entre la respectiva varianza:

(5)
$z_{ij} = \frac{x_{ij}}{\sigma'_{j}}$

donde $\{\sigma'_j\}$ son las desviaciones estándares muestrales (estimación de $\{\sigma_j\}$ ).

Y la matriz equivalente a (3) se denomina Matriz de Correlacion:

(6)
$Corr = \frac{1}{m-1} Z^\top Z$

# Gaussiana tri-variada no-correlacionada

m = 10000                             # número de datos (tamaño de la mustra)
n = 3                                # dimensión de cada dato
Med = np.array([10, 3, -.5])                         # vector de medias
Cov = np.array([[5, 0, 0], [0, 0.1, 0],[0, 0, 3]]) # Covarianza diagonal
X = np.random.multivariate_normal(Med, Cov, m)

from mpl_toolkits.mplot3d import Axes3D

def plotData3D(X, projection='3d'):
    fig = plt.figure(figsize=(12,4))  
    ax = fig.add_subplot(131, projection=projection)
    ax.scatter(X[:,0],X[:,0],X[:,2])
    ax.view_init(elev=10,azim=-30)       # Set rotation angle to 30 degrees
    ax.set_xlabel('$x_1$')
    ax.set_ylabel('$x_2$')
    ax.set_zlabel('$x_3$')
    ax.set_title('originales')  
    X -= np.mean(X, axis=0)           # resta la media 
    ax = fig.add_subplot(132, projection=projection)
    ax.scatter(X[:,0],X[:,0],X[:,2])
    ax.view_init(elev=10,azim=-30)       # Set rotation angle to 30 degrees
    ax.set_xlabel('$x_1$')
    ax.set_ylabel('$x_2$')
    ax.set_zlabel('$x_3$') 
    ax.set_title('centrados')
    X /= np.std(X, axis=0)            # divide entre la varianza
    ax = fig.add_subplot(133, projection=projection)
    ax.scatter(X[:,0],X[:,0],X[:,2])
    ax.view_init(elev=10,azim=-30)       # Set rotation angle to 30 degrees
    ax.set_xlabel('$x_1$')
    ax.set_ylabel('$x_2$')
    ax.set_zlabel('$x_3$') 
    ax.set_title('normalizados')
    plt.show()

plotData3D(X)

png

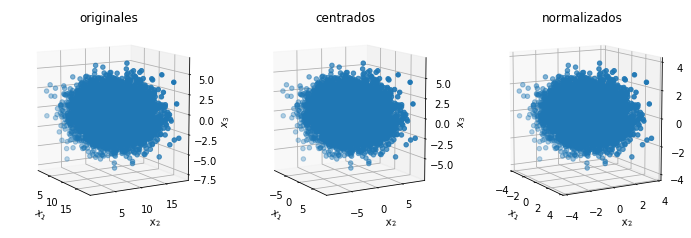
Aunque las tres figuras se ven iguales, nótese que los datos de originales no estan centrados (no tienen media cero) y solo solo normalizados tienen igual rango dinámico en las tres componentes de las variables

Esto la diferencia entre de los eigenvalores calculados usando datos centrados vs normalizados se muestra en los códigos que siguen, Notese que los eigenvectores prácticamente no son afectados, mayor aun para estos datos no correlacionados. Compárese con los datos correlacionados

Descomposición Valores Propios (Eig)

Sea $S = X^\top X$ la matriz de covarianza, definida semipositiva y simética, entonces, su descomposición eigenvalores $\mathrm{eig}\{S\}$ propios resulta en la forma:

(7)
$X^\top X = Q \Lambda Q^\top$
donde $\Lambda= \mathrm{diag(\lambda_1, \lambda_2,\ldots,\lambda_n)}$ es una matriz diagonal con entradas con los eigenvalores ordenados descendentemente: $\lambda_i \ge \lambda_{i+1} \ge 0$ ; las columnas de la matriz ortonormal

$Q = [ q_1, q_2\ldots,q_n ]$

son los vectores propios tal que el eigenvector $q_i$ esta asociado al eigenvalor $\lambda_i$ . Más aun, el eigenvalor $\lambda_i$ corresponde a la varianza de los datos a los largo del eje definido por el eigenvector $q_i$ .

En caso de variables Gaussianas no correlacionadas, los eigenvectores coincidiran con los la base canónica; i.e. $Q = Id.$

Note que, dada la forma de la descomposición (7), la matriz a descomponer tendrá que ser necesariamente cuadrada. Algunas matrices cuadradas implicarán factorizaciones complejas (en el sentido de reales e imaginarios). Pero todas la matrices reales, semipositivas definidas y simétricas (como las de covarianza) se pueden descomponer, que son las que nos interesan.

Descomposición Valores (SVD)

Sea $X$ una matriz de datos, no necesariamente cuadrada ( $m \ne n$

Entonces, su descomposición en eigenvalores no será posible. Pero, existe una forma alterna de descomposición, la descomposición en valores singulares $\mathrm{SVD}\{X\}$ :

(8)
$X = U D V^\top$
donde:

Los vectores singulares izquierdos de $X$ , $U = [ u_1, u_2\ldots,u_n ]$ , son los eigenvectores de $X X^\top$ :

(9)
$X X^\top = U D V^\top (U D V^\top)^\top \\ \;\;\;\; = U D V^\top (V D U^\top) \\ \;\;\;\; = U D^2 U^\top.\;\;\;\;\;\;\;\;\;$

Los vectores singulares derechos de $X$ , $V = [ v_1, v_2\ldots,v_n ]$ , son los eigenvectores $X^\top X$ :

(10)
$X^\top X = (U D V^\top)^\top U D V^\top \\ \;\;\;\; = (V D U^\top) U D V^\top \;\; \\ \; = V D^2 V^\top. \;\;\;\;\;\;\;\;\;\;\;\;$

$D = \mathrm{diag(d_1, d_2,\ldots,d_n)}$ una matriz diagonal con entradas con los valores singulares ordenados descendentemente: $d_i \ge d_{i+1} \ge 0$ ; Sus valores corresponden al cuadrado de los eigenvalores no-zero de ambas, $X X^\top$ y $X^\top X$ .

# Code source: Mariano Rivera
# mayo 2017

#-------------------------------------------------------------------
def EigSvd(X):
    X = X - np.mean(X, axis=0)
    S = X.T.dot(X)/(m-1) 
    print("Matriz de Covarianza:")
    printArray(S)
    print('_'*30)
    #------------------------------
    D, U = np.linalg.eig(S)
    print('eigenvalores X.T X = ')
    printArray(D,2)
    print('eigenvectores X.T X= ')
    printArray(U,2)
    print('_'*30)
    #------------------------------
    U, D, V = np.linalg.svd(S, full_matrices=True)
    print('SVD descomposición de X.T X : U D V')
    printArray(U,2)
    printArray(D,2)
    printArray(V,2)
    print('_'*30)#------------------------------
    U, D, V = np.linalg.svd(X, full_matrices=True)
    print('SVD descomposición de X ')
    print('Eingenvectores de X X.T')
    printArray(U,2)
    print('Eingenvalores mayores que cero de  (X X.T) o (X.T X)')
    printArray(np.sqrt(D))
    print('Eingenvectores de X.T X')
    printArray(V, 2, False)
    print('_'*30)
    
#-------------------------------------------------------------------  
EigSvd(X)

Matriz de Covarianza:
[[ 1.    -0.009  0.009]
 [-0.009  1.     0.003]
 [ 0.009  0.003  1.   ]]
______________________________
eigenvalores X.T X = 
[ 0.99  1.01  1.  ]
eigenvectores X.T X= 
[[-0.66 -0.75 -0.01]
 [-0.52  0.45  0.73]
 [ 0.54 -0.49  0.69]]
______________________________
SVD descomposición de X.T X : U D V
[[ 0.75 -0.01 -0.66]
 [-0.45  0.73 -0.52]
 [ 0.49  0.69  0.54]]
[ 1.01  1.    0.99]
[[ 0.75 -0.45  0.49]
 [-0.01  0.73  0.69]
 [-0.66 -0.52  0.54]]
______________________________
SVD descomposición de X 
Eingenvectores de X X.T
[[ 0.02 -0.   -0.02 ...,  0.01  0.02 -0.  ]
 [ 0.01  0.   -0.   ..., -0.    0.01  0.01]
 [ 0.01 -0.02  0.   ...,  0.01  0.    0.01]
 ..., 
 [-0.01  0.01  0.   ...,  1.   -0.   -0.  ]
 [-0.02 -0.01  0.01 ..., -0.    1.   -0.  ]
 [-0.01 -0.   -0.01 ..., -0.   -0.    1.  ]]
Eingenvalores mayores que cero de  (X X.T) o (X.T X)
[ 10.029  10.008   9.963]
Eingenvectores de X.T X
[[ 0.75 -0.45  0.49]
 [ 0.01 -0.73 -0.69]
 [-0.66 -0.52  0.54]]
______________________________

# Code source: Mariano Rivera
# mayo 2017

#-------------------------------------------------------------------
def pca_basico(X, varianzaExplicada=1):
    X = X - np.mean(X, axis=0)
    X = X / np.std(X, axis=0)
    corrMat=np.cov(X, rowvar=False)
    evals, evecs = np.linalg.eigh(corrMat)
    print("_"*30)
    print('PCA Código Básico')
    print("_"*30)
    print('Matriz de Correlación:')
    printArray(corrMat)
    evals, evecs = np.linalg.eigh(corrMat)
    # ordenando los eigenvalores de mayor a menor 
    # np.linalg.eig no los devuelve ordenados
    idx = np.argsort(evals)[::-1]   # indices ordenados
    evecsSorted = evecs[:,idx]      # Eigenvalores ordenados      
    evalsSorted = evals[idx]        # Eighenvectores ordenados
    varianzaAcumulada = np.cumsum(evalsSorted)/np.sum(evalsSorted)
    # indice de umbral de varianza retenida
    indexVar=np.argmax(varianzaAcumulada>=varianzaExplicada)
    evecsSorted = evecsSorted[:,:indexVar+1]
    # datos proyectados y reducidos
    Beta=np.dot(evecsSorted.T, X.T).T
    print('Eigenvalores')
    printArray(evalsSorted)
    print('Eigenvectores')
    printArray(evecsSorted)
    print("_"*30)
    
#-------------------------------------------------------------------    
def pca_with_sklean(X, varianzaExplicada=1.0): 
    print('PCA usando sklearn')
    clf=PCA(varianzaExplicada)
    X_train=X
    X_train=clf.fit_transform(X_train)
    print("_"*30)
    print('Eigenvalores')    
    printArray(clf.explained_variance_)
    print('Eigenvectores')
    printArray(clf.components_)
    print('Razón de explicación por componente:', clf.explained_variance_ratio_) 
    print(clf) 
    print("_"*30)

#-------------------------------------------------------------------    
pca_basico(X, varianzaExplicada=.98)
pca_with_sklean(X, varianzaExplicada=0.98)

______________________________
PCA Codigo Básico
______________________________
Matriz de Correlación:
[[ 1.    -0.009  0.009]
 [-0.009  1.     0.003]
 [ 0.009  0.003  1.   ]]
Eigenvalores
[ 1.012  1.003  0.985]
Eigenvectores
[[ 0.749 -0.014  0.662]
 [-0.447  0.727  0.521]
 [ 0.489  0.687 -0.538]]
______________________________
PCA usando sklearn
______________________________
Eigenvalores
[ 1.012  1.003  0.985]
Eigenvectores
[[ 0.749 -0.447  0.489]
 [ 0.014 -0.727 -0.687]
 [ 0.662  0.521 -0.538]]
Razón de explicación por componente: [ 0.33718644  0.33441098  0.32840258]
PCA(copy=True, iterated_power='auto', n_components=0.98, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)
______________________________

Distribución Gaussiana multivariada correlacionada

# Code source: Mariano Rivera
# mayo 2017

# Gaussiana tri-variada no-correlacionada
v= np.array([2,3,4]) 
v= v / np.sqrt(v.dot(v))
T = np.outer(v,v) +.2*np.eye(3)  # tensor definido positivo simético
L, R = np.linalg.eig(T)
# R es la matriz de rotacion que nos interesa, 
# L tienen eigenvalores delk tensor, pero vamos a reemplazarlos 

# matriz de correlacion generada con varianzas                
# (eigenvalores) igual al caso no correlacionado  
CovC = R.dot(np.diag(D).dot(R.T))

print('Covarianza con datos correlacionados: Def. positiva y simétrica')
printArray(CovC)
D, U = np.linalg.eig(CovC)
print('Eigenvalores:')
printArray(D)
print('EigenVectores:')
printArray(U)

m = 300                             # número de datos (tamaño de la mustra)
n, nn = CovC.shape                              # dimensión de cada dato
Med = np.array([1, 2, -10])                         # vector de medias
X = np.random.multivariate_normal(Med, CovC, m)

Covarianza con datos correlacionados: Def. positiva y simétrica
[[ 1.325 -0.212 -0.299]
 [-0.212  0.209  0.257]
 [-0.299  0.257  0.367]]
Eigenvalores:
[ 1.471  0.41   0.019]
EigenVectores:
[[ 0.928 -0.371  0.007]
 [-0.217 -0.557 -0.802]
 [-0.301 -0.743  0.598]]

plotData3D(X)

png

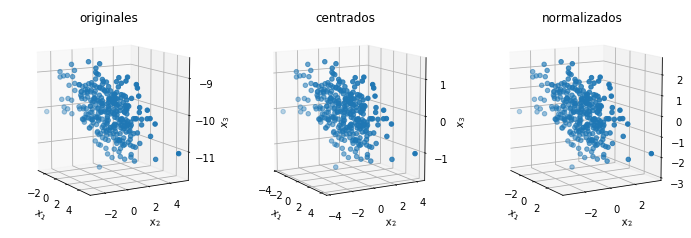
 EigSvd(X)

Matriz de Covarianza:
[[ 1.003 -0.385 -0.397]
 [-0.385  1.003  0.927]
 [-0.397  0.927  1.003]]
______________________________
eigenvalores X.T X = 
[ 2.19  0.75  0.08]
eigenvectores X.T X= 
[[ 0.42 -0.91  0.01]
 [-0.64 -0.31 -0.7 ]
 [-0.64 -0.29  0.71]]
______________________________
SVD descomposición de X.T X : U D V
[[-0.42 -0.91  0.01]
 [ 0.64 -0.31 -0.7 ]
 [ 0.64 -0.29  0.71]]
[ 2.19  0.75  0.08]
[[-0.42  0.64  0.64]
 [-0.91 -0.31 -0.29]
 [ 0.01 -0.7   0.71]]
______________________________
SVD descomposición de X 
Eingenvectores de X X.T
[[ 0.    0.01  0.02 ..., -0.01  0.03  0.01]
 [-0.04  0.09  0.08 ...,  0.07 -0.06  0.17]
 [-0.02 -0.04 -0.08 ..., -0.06  0.02 -0.08]
 ..., 
 [-0.06 -0.05 -0.05 ...,  0.99  0.   -0.01]
 [ 0.06  0.02  0.01 ...,  0.01  1.    0.01]
 [-0.12 -0.13 -0.06 ..., -0.01  0.01  0.97]]
Eingenvalores mayores que cero de  (X X.T) o (X.T X)
[ 5.057  3.864  2.187]
Eingenvectores de X.T X
[[-0.42  0.64  0.64]
 [ 0.91  0.31  0.29]
 [ 0.01 -0.7   0.71]]
______________________________

pca_basico(X, varianzaExplicada=.98)
pca_with_sklean(X, varianzaExplicada=0.98)

______________________________
PCA Código Básico
______________________________
Matriz de Correlación:
[[ 1.003 -0.385 -0.397]
 [-0.385  1.003  0.927]
 [-0.397  0.927  1.003]]
Eigenvalores
[ 2.188  0.746  0.077]
Eigenvectores
[[-0.423  0.906  0.011]
 [ 0.64   0.307 -0.705]
 [ 0.642  0.291  0.709]]
______________________________
PCA usando sklearn
______________________________
Eigenvalores
[ 2.181  0.743  0.076]
Eigenvectores
[[-0.423  0.64   0.642]
 [-0.906 -0.307 -0.291]
 [-0.011  0.705 -0.709]]
Razón de explicación por componente: [ 0.72688877  0.2476747   0.02543653]
PCA(copy=True, iterated_power='auto', n_components=0.98, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)
______________________________

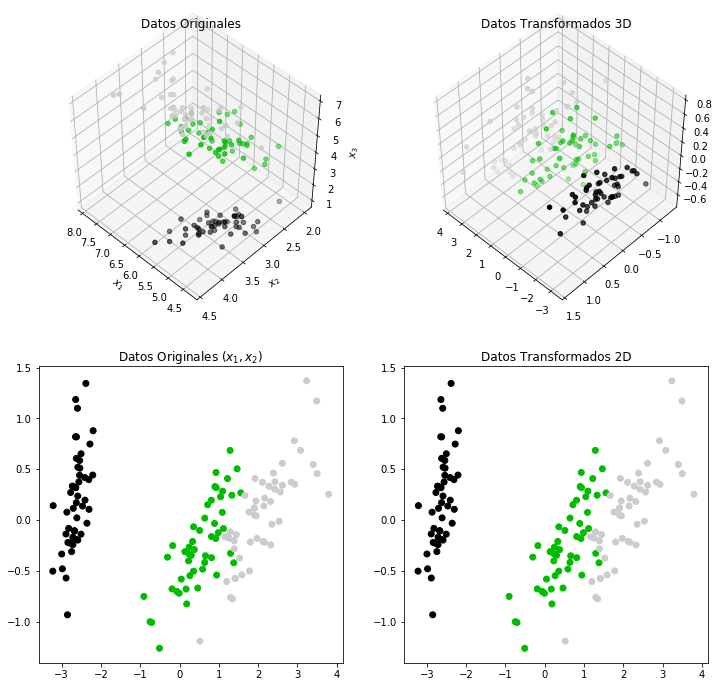
Ejemplo de reducción de Dimensionalidad usando PCA

Basado en el ejemplo de código mas elaborado en sklearn por Gaël Varoquaux, License BSD 3 clause.

# Code source: Mariano Rivera
# mayo 2017

import numpy as np
import matplotlib.pyplot as plt
from sklearn import decomposition
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target

pca = decomposition.PCA(n_components=3)
pca.fit(X)
Xt = pca.transform(X)

pca2 = decomposition.PCA(n_components=2)
pca2.fit(X)
Xt2 = pca2.transform(X)

fig = plt.figure(1, figsize=(12, 12))

ax = fig.add_subplot(221, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.spectral)
ax.view_init(elev=48,azim=134)
ax.set_title('Datos Originales') 
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('$x_3$')
    
ax = fig.add_subplot(222, projection='3d')
ax.scatter(Xt[:, 0], Xt[:, 1], Xt[:, 2], c=y, cmap=plt.cm.spectral)
ax.view_init(elev=48,azim=134)
ax.set_title('Datos Transformados 3D') 

ax = fig.add_subplot(223) #, projection='2d')
ax.scatter(Xt[:, 0], Xt[:, 1], c=y, cmap=plt.cm.spectral)
#ax.view_init(elev=48,azim=134)
ax.set_title('Datos Originales $(x_1,x_2)$') 

ax = fig.add_subplot(224) #, projection='2d')
ax.scatter(Xt2[:, 0], Xt2[:, 1], c=y, cmap=plt.cm.spectral)
#ax.view_init(elev=48,azim=134)
ax.set_title('Datos Transformados 2D')
plt.show()

png