Código
2 Modelo de regresión Lineal
2.1 Introducción
2.1.1 Problemas en regresión
- modelar (de alguna forma) la relación entre la entrada y la salida de un sistema.
- predecir y para un conjunto dado de covariables.
- evaluar y comparar el impacto de diferentes covariables sobre la respuesta.
En algunos casos es posible tener el grado de conocimiento del fenómeno, de forma que se puede escribir explícitamente un modelo matemático que describe el comportamiento del mismo \[ y=f\left(x_1, x_2, \cdots, x_p\right) \] Sin embargo, las técnicas de análisis que veremos se refieren precisamente al caso en el que no tenemos tal detalle de conocimiento (salvo cuando veamos regresión nolineal).
2.1.2 La regresión
En términos generales “la regresión” es el estudio de la distribución condicional de \(Y|\boldsymbol{X}\) donde \(\boldsymbol{X}=x_1,\ldots, x_p\). Particularmente, algunos de sus objetivos son:
- Establecer una relación entre la variable de respuesta \(Y\) y variables de “entrada” (covariables) \(\boldsymbol{X}_{p}\).
- Comparar el impacto de \(\boldsymbol{X}_{p}\) sobre la respuesta \(y\).
- Predecir \(Y\) basado en un conjunto de valores de \(\boldsymbol{x}_{p}\).
2.1.3 Un poco de historia
El término “regresión” y los métodos para investigar las relaciones entre dos variables puede remontarse a hace unos 100 años.
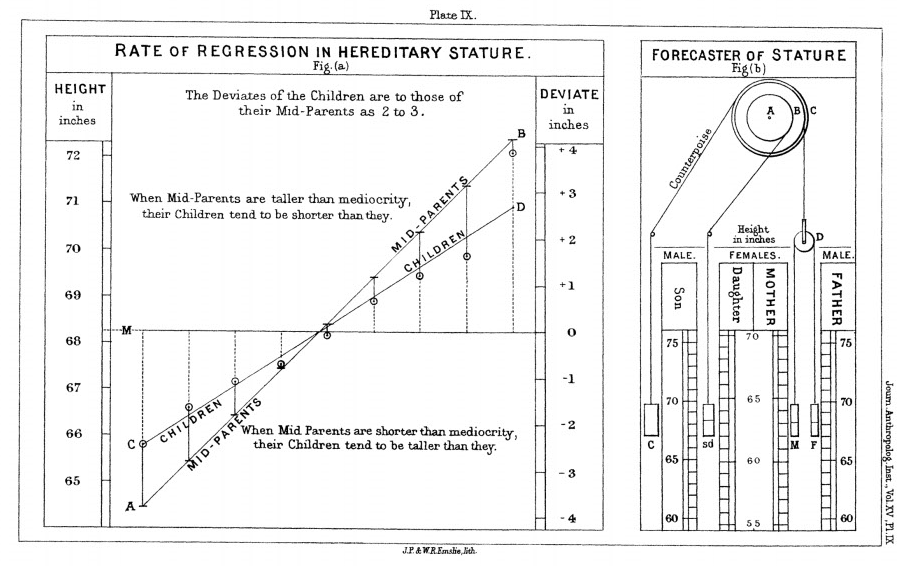
El nombre fue introducido por Francis Galton en 1908, el reconocido biólogo británico, cuando se dedicaba al estudio de la herencia. Primo de Charles Darwin, aplicó sus principios a numerosos campos, principalmente al estudio del ser humano y a las diferencias individuales. En 1901, fue, junto con Karl Pearson y Walter Weldon, cofundador de la revista científica Biometrika.
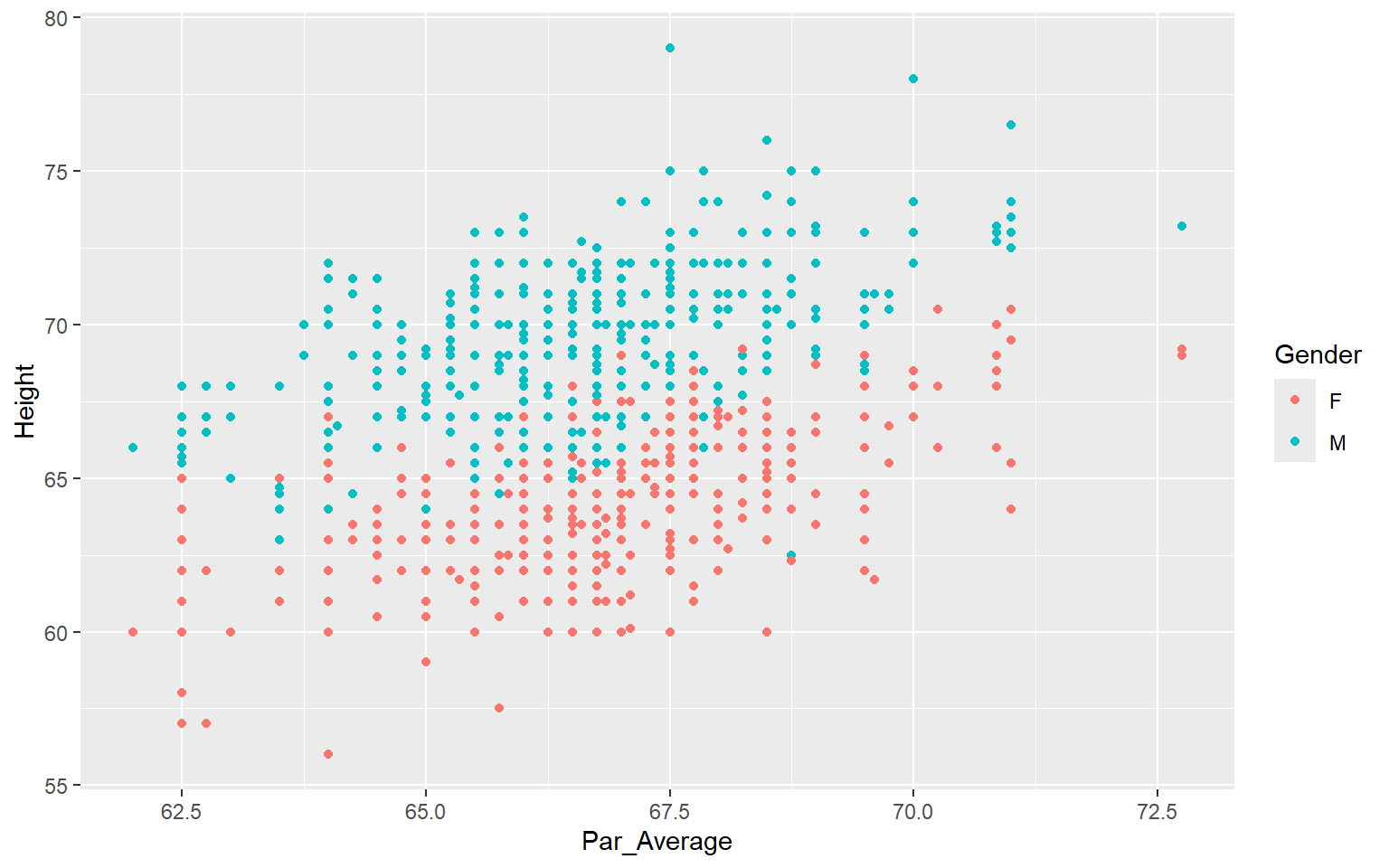
Una de sus observaciones fue que la altura de los hijos de padres altos no se transmiten por completo a su descendencia. Más bien, las características de la descendencia retroceden o “regresan” hacia un punto “mediocre” (un punto que desde entonces ha sido identificado como la media). Al medir las alturas de cientos de personas, fue capaz de cuantificar la regresión a la media, y estimar el tamaño del efecto. Esta “regresión hacia la mediocridad” dio nombre a estos métodos estadísticos.
Ejemplo: Datos de altura de Galton
Código
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
dat = pd.read_csv("data/Datos_Galton.csv")
dat['Par_Average'] = (dat['Father'] + dat['Mother']) / 2
plt.figure(figsize=(10, 6))
sns.scatterplot(data=dat, x='Par_Average', y='Height', hue='Gender', palette='viridis')
plt.show()
2.2 Estructura del modelo
Sea \(Y\) la variable de interés, que también se conoce como variable respuesta, objetivo o dependiente.
2.2.1 Modelo de regresión simple
Este modelo considera unicamente una covariable \(X\). A esta variable también se le conoce como variable explicativa o antes se denominaba como variable independiente.
Si consideramos el conjunto de \(n\) diferentes observaciones \((X_1,Y_1),\ldots (X_n,Y_n)\), podemos definir el modelo para cada una de forma matricial.
El modelo es: \[ Y_i=\beta_0+\beta_1 X_i+\epsilon_i, \qquad i=1,\ldots, n \] donde \(\beta_0\) es el intercepto (ordenada al origen), \(\beta_1\) es la pendiente de la línea y \(\epsilon_i\) es el error aleatorio de cada observación. El supuesto más común es que las \(\{X_i\}\) son v.a. i.i.d. con media 0 y varianza constante.
2.2.2 Modelo de regresión (múltiple)
El modelo de regresión múltiple tiene \(k\geq 2\) variables explicativas y para \(n\) observaciones se plantea como \[ Y_i=\beta_0+\beta_1 X_{i1}+\cdots+\beta_k X_{ik}+\epsilon_i \qquad i=1,\ldots,n. \] Nótese que el número de variables a estimar es \(p=k+1\) ya que aunque tenemos \(k\) covariables, también tenemos que estimar \(\beta_0\).
Este modelo lo podemos plantear de forma matricial considerando: \[ \boldsymbol{Y}=\left[\begin{array}{c} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{array}\right], \quad \boldsymbol{X_j}=\left[\begin{array}{c} X_{1j} \\ X_{2j} \\ \vdots \\ X_{nj} \end{array}\right], \ j=1,\ldots,k \quad \boldsymbol{\beta}=\left[\begin{array}{c} \beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{k} \end{array}\right], \quad \boldsymbol{\epsilon}=\left[\begin{array}{c} \epsilon_{1} \\ \epsilon_{2} \\ \vdots \\ \epsilon_{n} \end{array}\right], \] y la matriz \(X\) con columnas \[ X=\left(\boldsymbol{1},\boldsymbol{X}_1, \ldots, \boldsymbol{X_k}\right), \] es de dimensión \(n \times (k+1) = n\times p\). como \[ \boldsymbol{Y} = X \boldsymbol{\beta}+\boldsymbol{\epsilon}. \]
En ambos casos es usual asumir \(\epsilon_i\) son i.i.d., con \(\epsilon_1 \sim \mathrm{N}\left(0, \sigma^2\right)\).
Esto hace que para \(X\) fija, \(Y\) sea una vector aleatorio con media \[ \mathbb{E}(Y)=X \boldsymbol{\beta} \ \ \ \ \mbox{y varianza}\ \ \ \ \Sigma=\sigma^2\ I_{n}, \] donde \(I_{n}\) es la matriz identidad con \(n\) renglones y columnas.
Ejemplo: Como se ve datos con el modelo lineal simple
Código
library(ggplot2)
set.seed(19)
n <- 1000 # tamaño de la muestra
x <- runif(n,0,10) # simulamos datos
y <- 1.6 + 2.5 * x + rnorm(n, 0, sd = 1) #sd=1
dat <- data.frame(x=x,y=y)
ggplot(dat, aes(x = x, y = y)) + geom_point()
y <- 1.6 + 2.5 * x + rnorm(n,0,sd = 5) #sd=1
dat <- data.frame(x = x, y = y)
ggplot(dat, aes(x = x, y = y)) + geom_point()
Código
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(19)
n = 1000 # Tamaño de la muestra
x = np.random.uniform(0, 10, n) # simulamos datos
y1 = 1.6 + 2.5 * x + np.random.normal(0, 1, n)
dat1 = pd.DataFrame({'x': x, 'y': y1})
plt.figure(figsize=(10, 6))
sns.scatterplot(data=dat1, x='x', y='y')
plt.title("Scatter plot with sd=1")
plt.show()
y2 = 1.6 + 2.5 * x + np.random.normal(0, 5, n)
dat2 = pd.DataFrame({'x': x, 'y': y2})
plt.figure(figsize=(10, 6))
sns.scatterplot(data=dat2, x='x', y='y')
plt.title("Scatter plot with sd=5")
plt.show()
2.3 Estimadores suficientes
Una estadística suficiente se define en relación con un modelo estadístico, generalmente un modelo paramétrico, y proporciona toda la información en los datos sobre ese modelo o sus parámetros \(\boldsymbol{\beta}\).
En muchos casos, la estadística suficiente proporciona una reducción sustancial de la complejidad o dimensión de los datos originales, y como resultado, el concepto de suficiencia hace que la tarea de la inferencia estadística sea más simple.
La suficiencia de un estadístico o estimador significa que los datos completos no proporcionan información adicional sobre \(\boldsymbol{\beta}\) dado el estimador.
Si aquí falla la condición de rango completo, entonces \(\boldsymbol{\beta}\) no es identificable. Esto significa que existe un \(\boldsymbol{\beta}^{\star}\) diferente de \(\boldsymbol{\beta}\) tal que \(P_{\boldsymbol{\beta}}(Y\leq t)=P_{\boldsymbol{\beta^{\star}}}(y\leq t)\) para todo \(t\). Los datos en su totalidad no son informativos sobre si el parámetro es igual a \(\boldsymbol{\beta}\) o \(\boldsymbol{\beta}^{\star}\).
Definición 2.1 (Identificabilidad de un modelo) El parámetro \(\theta\) es identificable si para cualquier \(\theta_1\) y \(\theta_2\), \(f(\theta_1) = f(\theta_2)\) implica que \(\theta_1 = \theta_2\). Si \(\theta\) es identificable, decimos que la parametrización \(f(\theta)\) es identificable. Además, una función vectorial \(g(\theta)\) es identificable si \(f(\theta_1) = f(\theta_2)\) implica que \(g(\theta_1) = g(\theta_2)\). Si la parametrización no es identificable pero existen funciones identificables no triviales, entonces se dice que la parametrización es parcialmente identificable.
Una de las maneras más simples de verificar la suficiencia es observando directamente la log-verosimilitud y utilizando el teorema de factorización. Realizamos este análisis en la Sección 2.5.
2.4 Estimación via mínimos cuadrados
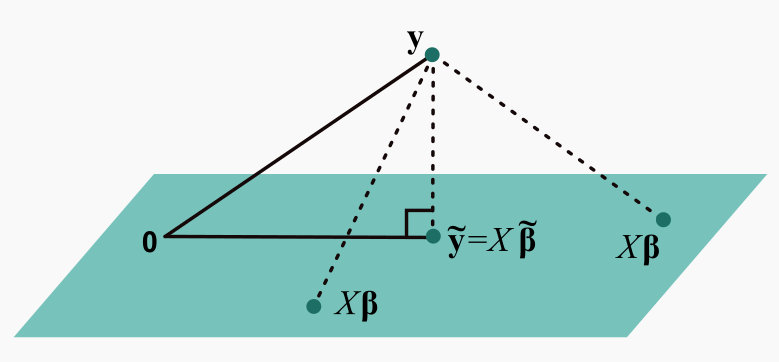
Proposición 2.1 (Estimador de mínimos cuadrados) Si \(X\) es de rango completo (\(\operatorname{rango}({X})=p\)) el único estimador de \(\boldsymbol{\beta}\) que minimiza la función ‘Suma de cuadrada de los errores residuales’ : \[ \begin{aligned} SS_{\operatorname{Res}}(\boldsymbol{\beta})&=\sum_{i=1}^n\left(y_i-[X\boldsymbol{\beta}\right]_i)^2\\ &=({y}-{X} \boldsymbol{\beta})^{\top}(\boldsymbol{y}-{X} \boldsymbol{\beta})=||\boldsymbol{y}-{X} \boldsymbol{\beta}||^2 \end{aligned} \]
es \(\qquad \qquad \widetilde{\boldsymbol{\beta}} =(X^{\top}X)^{-1}X^{\top}\boldsymbol{y}\).
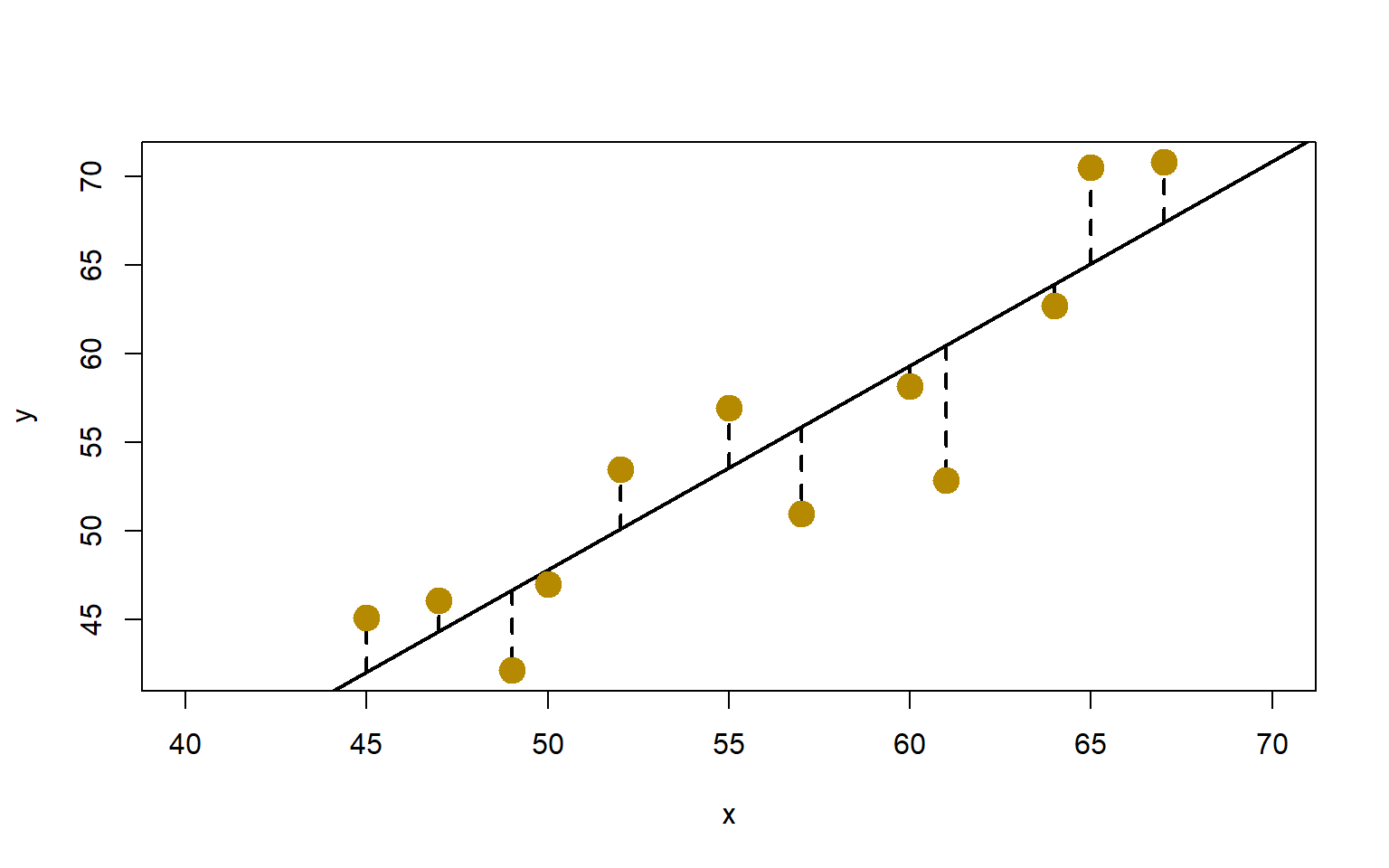
Otra forma en que se puede derivar \(\widetilde{\beta}\) es que cuando \(\boldsymbol{\beta}\) varía, \(X \boldsymbol{\beta}\) determina el subespacio de \(\mathbb{R}^n\) generado por las columnas de \(X\), de modo que \(\|y-X \beta\|\) es la distancia de \(y\) al plano determinado por las columnas de \(X\), sabemos que el vector que minimiza esta distancia es la proyección, de \(y\) sobre ese plano, así que esta proyección \(v\) debe ser de la forma \(v=X \widetilde{\beta}\). Ahora, \(y-v\) debe ser ortogonal a todos los vectores del plano, esto es \((y-v) \perp X \boldsymbol{\beta}\) para todo \(\boldsymbol{\beta}\). Entonces \((y-X \widetilde{\beta})^{\top} X \boldsymbol{\beta}=0\) para toda \(\boldsymbol{\beta}\), de modo que se debe cumplir las ecuaciones normales \(X^{\top} X \widetilde{\beta}=X^{\top} y\). De aquí que \(\widetilde{\beta}=\left(X^{\top} X\right)^{-1} X^{\top} y\).
¿ Y si \(X^{\top} X\) no es invertible?
En este caso el sistema no tiene solución o tiene infinitas soluciones. Sin embargo alguna solución siempre existe para las ecuaciones normales, por lo que se tienen infinitas de ellas.
En regresión lineal no todo lo que se ajusta es “plano”
2.5 Estimadores máximo verosímiles
Para un modelo de regresión lineal \[ \boldsymbol{Y}=X\boldsymbol{\beta}+\boldsymbol{\epsilon} \] con un \(\boldsymbol{\epsilon} \sim N(\boldsymbol{0},\sigma^2 I_n)\), la función de verosimilitud puede escribirse como: \[ \begin{aligned} L(\beta,\sigma;X,\boldsymbol{y}) &= \prod_{i=1}^n \frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{\left(y_i-[X\boldsymbol{\beta}]_i\right)^2}{2\sigma^2}\right\}\\ &=\frac{1}{(2\pi\sigma^2)^{n/2}} \exp\left\{-\sum_{i=1}^n \frac{\left(y_i-[X\boldsymbol{\beta}]_i\right)^2}{2\sigma^2}\right\}\\ &=\frac{1}{(2\pi\sigma^2)^{n/2}} \exp\left\{ -\frac{\left(\boldsymbol{y}-X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{y}-X\boldsymbol{\beta}\right)}{2\sigma^2}\right \}. \end{aligned} \]
2.5.1 Suficiencia
Entonces la log-verosimilitud es \[ \begin{aligned} \ell(\beta,\sigma;X,\boldsymbol{y}) &=c-n\ln\sigma-\left\{\frac{\left(\boldsymbol{y}-X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{y}-X\boldsymbol{\beta}\right)}{2\sigma^2}\right \}\\ & =c-n \ln \sigma-\frac{1}{2 \sigma^2}\left(\boldsymbol{y}^{\top} \boldsymbol{y}-\boldsymbol{y}^{\top} X \boldsymbol{\beta}-\boldsymbol{\beta}^{\top} X^{\top} \boldsymbol{y}+\boldsymbol{\beta}^{\top} X^{\top} X \boldsymbol{\beta}\right) \\ & =c-n \ln \sigma-\frac{1}{2 \sigma^2} \boldsymbol{y}^{\top} \boldsymbol{y}-\frac{1}{2 \sigma^2}\left(2 \boldsymbol{\beta}^{\top} \mathbf{T}_1-\boldsymbol{\beta}^{\top} \mathbf{T}_2 \boldsymbol{\beta}\right) \\ & =h(\boldsymbol{y}, \sigma)+g_{\boldsymbol{\beta}}\left(\mathbf{T}_1, \mathbf{T}_2, \sigma\right),\\[15pt] \end{aligned} \] donde $_1 = _1(X, ) = X^{} $ y \(\ \mathbf{T}_2 = \mathbf{T}_2(X, \boldsymbol{y}) = X^{\top} X\). Esto muestra que el estadistico \(\mathbf{T} \equiv\left(\mathbf{T}_1, \mathbf{T}_2\right)\) es suficiente para \(\boldsymbol{\beta}\).
Para este resultado no se requiere que \(X\) tenga rango completo, pero como hemos comentado, cuando no se tiene esta característica de \(X\), el estadístico \(\mathbf{T}\) no es minimal suficiente.
De la log-verosimilitud vemos también que el estadístico suficiente para \(\sigma\) es \((n, \operatorname{SCE}(\boldsymbol{\beta})).\)
2.5.2 Estimadores Máximo Verosímiles
2.5.2.1 Estimador de \(\boldsymbol{\beta}\)
Para obtener el EMV de \(\boldsymbol{\beta}\), \(\widehat{\boldsymbol{\beta}}\), observamos que la log-verosimilitud marginal es \[ \begin{aligned} \ell(\beta, \sigma^2;X,\boldsymbol{Y}) &=-\frac{n}{2}\ln(2\pi\sigma^2)-\frac{1}{2\sigma^2}\left\{\left(\boldsymbol{Y}-X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}-X\boldsymbol{\beta}\right)\right\}\\ &=c-\frac{1}{2\sigma^2}\left\{\left(\boldsymbol{Y}-X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}-X\boldsymbol{\beta}\right)\right\} \end{aligned} \] como \(c\) y son funcionalmente independiente de \(\beta\) y escalares positivos, tenemos que \[ \widehat{\boldsymbol{\beta}}=\text{arg max}_{\boldsymbol{\beta}} \ \ \ell(\beta;X,\boldsymbol{Y},\sigma) =\text{arg min}_{\boldsymbol{\beta}} \left\{\left(\boldsymbol{Y}-X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}-X\boldsymbol{\beta}\right)\right\} \ \ \] que coincide con el problema de minimizar la función SCE\((\beta)\) que planteamos en la estimación de mímimos cuadrados. Por lo tanto \(\widehat{\beta}=\widetilde{\beta}\).
2.5.2.2 Estimador de \(\sigma^2\)
Ahora calculamos el EMV de \(\sigma^2\), \(\widehat{\sigma}^2\), obteniendo la parcial de la log-verosimilitud e igualando a 0. \[ \begin{aligned} \frac{\partial}{\partial \sigma^2}\ell(\beta, \sigma^2;X,\boldsymbol{Y})&=\frac{\partial}{\partial \sigma^2} \left[-\frac{n}{2} \ln(2\pi \sigma^2)- \frac{1}{2 \sigma^2}\left(\boldsymbol{Y}-X \boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right)\right] \\ &=-\frac{n}{2 \sigma^2}+\frac{1}{2 \sigma^4}\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right) =0\\ \Leftrightarrow \ \ \ \ \ \ \ \ \ \ \ &-n+\frac{1}{\sigma^2}\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right) =0 \\ \Leftrightarrow \ \ \ \ \ \ \ \sigma^2 & =\frac{1}{n}\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}-X \boldsymbol{\beta}\right). \end{aligned} \] Como \(\partial^2/\partial (\sigma^2)^2\ \ \ell(\beta, \sigma^2;X,\boldsymbol{Y})=-1/\sigma^4\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right)^{\top}\left(\boldsymbol{Y}- X\boldsymbol{\beta}\right)<0\), tenemos que \[ \widehat{\sigma}^2=\frac{1}{n}\left(\boldsymbol{Y}- X\widehat{\boldsymbol{\beta}}\right)^{\top}\left(\boldsymbol{Y}-X \boldsymbol{\widehat{\beta}}\right). \]
2.5.2.3 Definiciones y resultados
Teorema 2.1 (Propiedades del EMV \(\widehat{\boldsymbol{\beta}}\)) El estimador \(\widehat{\boldsymbol{\beta}}=\left(X^{\top}X\right)^{-1} X^{\top} \boldsymbol{Y}\) es un estimador insesgado de \(\boldsymbol{\beta}\) y su varianza es igual a
\[ \operatorname{Var}(\widehat{\boldsymbol{\beta}})=\left(X^{\top} X\right)^{-1} \sigma^2. \]
Observación 2.1. Como \(\boldsymbol{Y}\sim N(\boldsymbol{0},\sigma^2I_n)\), junto con los resultados anteriores, tenemos que \(\widehat{\boldsymbol{\beta}}\sim N\left(\boldsymbol{\beta},\ \left(X^{\top} X\right)^{-1} \sigma^2\right).\)
Sea \(\widehat{{Y}}=X \widehat{\boldsymbol{\beta}}\) el vector (de longitud \(n\)) de los valores ajustados de \(\boldsymbol{Y}.\) Esto es, \[ \widehat{\boldsymbol{Y}}=X \widehat{\boldsymbol{\beta}}=X\left(X^{\top} X\right)^{-1} X^{\top} \boldsymbol{Y} \]
Definición 2.2 (Matriz de proyección (Matriz gorro)) Si definimos como \(P=X\left(X^{\top} X\right)^{-1} X^{\top}\), entonces podemos escribir \[ \widehat{\boldsymbol{Y}} = P\boldsymbol{Y} \] La matriz \(P\) se denomina comúnmente como la “matriz gorro” (‘hat matrix’) y tiene las propiedades de ser simétrica e idempotente (\(A=A^{\top}\) y \(A^2=A\)).
La matriz \(P\) es matriz de proyección y por lo tanto también su complemento, \((I_n-P)\), es idempotente. Por otro lado, como \(P\) es simétrica, \(P\) es una proyección ortogonal.
Como \(\widehat{\boldsymbol{Y}}=X\left(X^{\top} X\right)^{-1} X^{\top} \boldsymbol{Y}=P\boldsymbol{Y}\) y \[ \mathbb{E}(\widehat{\boldsymbol{Y}})=\mathbb{E}(P\boldsymbol{Y})=P\mathbb{E}(\boldsymbol{Y})=PX\boldsymbol{\beta}=X\boldsymbol{\beta}, \] así como \[ \operatorname{Var}(\widehat{\boldsymbol{Y}})=\operatorname{Var}(X\widehat{\boldsymbol{\beta}})=X \operatorname{Var}(\widehat{\boldsymbol{\beta}})X^{\top} =X \left(X^{\top}X\right)^{-1}\sigma^2X^{\top}=P\sigma^2, \] entonces \(\widehat{\boldsymbol{Y}} \sim N(X\boldsymbol{\beta},P\sigma^2)\).
La varianza de un subconjunto de \(\widehat{\boldsymbol{Y}}\), \(\widehat{\boldsymbol{Y}}_r\), \(r \subset \{1,\ldots,n\}\), se puede determinar usando los renglones de \(X\) correspondientes. Sean esta matriz \(X_r\). Entonces \[ \operatorname{Var}(\widehat{\boldsymbol{Y}}_r)=X_r(\operatorname{Var}(\widehat{\boldsymbol{\beta}}))X_r^{\top}=X_r\left(X^{\top}X\right)^{-1}X_r^{\top}\sigma^2. \]
Definición 2.3 (Residuales) Los residuales del modelo ajustado \(\boldsymbol{\epsilon}\) se definen como \[ \boldsymbol{e}=\boldsymbol{Y}-\widehat{\boldsymbol{Y}} = I_n \boldsymbol{Y}-PY=\left(I_n-P\right) \boldsymbol{Y} \]
donde \(I_n\) es la matriz identidad.
Los residuales son una medida de la discrepancia de los verdaderos valores y los ajustados. Además,
Proposición 2.2
- El valor esperado de los residuales es cero, ya que \[ \mathbb{E}(\boldsymbol{e})=\mathbb{E}\left[(I_n-P)\boldsymbol{Y}\right]=(I_n-P)X\boldsymbol{\beta}=X\boldsymbol{\beta}-X\boldsymbol{\beta}=\boldsymbol{0}, \]
- y como \((I_n-P)\) es simétrica e idempotente, \[ \operatorname{Var}(\boldsymbol{e})=(I_n-P)\operatorname{Var}\left(\boldsymbol{Y}\right)(I_n-P)^{\top}=(I_n-P)(I_n-P)\sigma^2=(I_n-P)\sigma^2. \]
- Entonces \(\boldsymbol{e}\sim N(\boldsymbol{0},\ (I_n-P)\sigma^2)\).
- Por otro lado, como \(\boldsymbol{e}=(I_n-P)\boldsymbol{Y}\), entonces para cualquier vector \(\boldsymbol{w}\in \mathcal{C}(X)\), \(\boldsymbol{w}^{\top}\boldsymbol{e}=\boldsymbol{w}^{\top}(I_n-P)\boldsymbol{Y}=0\) ya que \(\mathcal{C}(X) \perp \mathcal{C}(I_n-P)\). Estos son dos casos relevantes:
\(\boldsymbol{1}_n^{\top}\boldsymbol{e}=\sum_{i=1}^ne_i=0\) si \(X\) contiene la columna de unos que corresponden a la ordenada del origen.
\(\widehat{\boldsymbol{Y}}^{\top}\boldsymbol{e}=\sum_{i=1}^n\widehat{Y}_ie_i=0\).
Dada la expresión del EMV de \(\sigma^2\), nos interesa la suma de los residuales cuadrados: \[ \begin{aligned} \sum_{i=1}^n e_i^2 =\boldsymbol{e}^{\top} \boldsymbol{e} & =\left[\left(I_n-P\right) \boldsymbol{Y}\right]^{\top}\left(I_n-P\right) \boldsymbol{Y}\\ & =\boldsymbol{Y}^{\top}\left(I_n-P\right)^{\top}\left(I_n-P\right) \boldsymbol{Y}\\ & =\boldsymbol{Y}^{\top}\left(I_n-P\right) \boldsymbol{Y}.\\ \end{aligned} \tag{2.2}\] En inglés esta función se llama “residual sum of squares” y se abreviar como RSS o \(SS_{\mathrm{Res}}\). Optaremos por esta segunda opción. Se puede demostrar fácilmente que \(SS_{\mathrm{Res}}\) es también igual a \[ SS_{\mathrm{Res}} =\boldsymbol{Y}^{\top}\boldsymbol{Y}-\widehat{\boldsymbol{Y}}^{\top}\widehat{\boldsymbol{Y}}. \]
La estimación basada en la verosimilitud produce el EMV de \(\sigma^2\): \[ \widehat{\sigma}^2=\frac{\left(\boldsymbol{Y}- X\widehat{\boldsymbol{\beta}}\right)^{\top}\left(\boldsymbol{Y}-X \boldsymbol{\widehat{\beta}}\right)}{n} = \frac{\boldsymbol{e}^{\top} \boldsymbol{e}}{n} \] no es estimador insesgado de \(\sigma^2\), pero sí lo es \(s^2=\boldsymbol{e}^{\top} \boldsymbol{e}/(n-p).\)
Teorema 2.2 (Estimador insesgado de \(\sigma^2\)) El estimador insesgado de \(\sigma^2\) es \[ s^2=\frac{\boldsymbol{e}^{\top} \boldsymbol{e}}{n-p}=\frac{\boldsymbol{Y}^{\top}\left(I_n-P\right) \boldsymbol{Y}}{n-p}=\frac{1}{n-p} \sum_{i=1}^n\left(Y_i-\widehat{Y}_i\right)^2. \]
Ejemplo: Ajuste de un modelo lineal
Código
#|
autompg <- read.table(
"http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data",
quote = "\"", comment.char = "", stringsAsFactors = FALSE)
colnames(autompg) <- c("mpg", "cyl", "disp", "hp", "wt", "acc", "year", "origin", "name")
autompg <- subset(autompg, autompg$hp != "?")
autompg <- subset(autompg, autompg$name != "plymouth reliant")
rownames(autompg) <- paste(autompg$cyl, "cylinder", autompg$year, autompg$name)
autompg <- subset(autompg, select = c("mpg", "cyl", "disp", "hp", "wt", "acc", "year"))
autompg$hp <- as.numeric(autompg$hp)
library(lattice)
library(RColorBrewer)
#display.brewer.all()
myColours <- brewer.pal(5,"Paired")
my.settings <- list(superpose.symbol=list(col=myColours, pch=19))
xyplot(mpg ~ wt | factor(year), data = autompg, groups = factor(cyl,labels=c("3","4","5","6","8")), col= myColours, pch=19, cex=1, auto.key =list(space="top", columns=5, title="cyl", cex.title=1), par.settings = my.settings)
Código
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Leer los datos
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data"
column_names = ["mpg", "cyl", "disp", "hp", "wt", "acc", "year", "origin", "name"]
autompg = pd.read_csv(url, delim_whitespace=True, names=column_names, na_values="?")
# Filtrar los datos
autompg = autompg.dropna(subset=["hp"])
autompg = autompg[autompg["name"] != "plymouth reliant"]
autompg["hp"] = autompg["hp"].astype(float)
# Renombrar los índices
autompg.index = autompg.apply(lambda row: f"{int(row['cyl'])} cylinder {int(row['year'])} {row['name']}", axis=1)
# Seleccionar las columnas necesarias
autompg = autompg[["mpg", "cyl", "disp", "hp", "wt", "acc", "year"]]
# Crear la figura y establecer el tamaño
plt.figure(figsize=(10, 10))
# Graficar los datos
myColours = sns.color_palette("Paired", 5)
g = sns.FacetGrid(autompg, col="year", hue="cyl", palette=myColours, col_wrap=4, height=4)
g.map(sns.scatterplot, "wt", "mpg", alpha=0.7)
Código
g.add_legend(title="cyl")
Código
plt.show()
#>
#> Call:
#> lm(formula = mpg ~ wt, data = autompg)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -11.9646 -2.7519 -0.3602 2.1597 16.5284
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 46.1983950 0.8021249 57.59 <2e-16 ***
#> wt -0.0076430 0.0002588 -29.53 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 4.343 on 388 degrees of freedom
#> Multiple R-squared: 0.6921, Adjusted R-squared: 0.6913
#> F-statistic: 872 on 1 and 388 DF, p-value: < 2.2e-16Código
names(model)#> [1] "coefficients" "residuals" "effects" "rank"
#> [5] "fitted.values" "assign" "qr" "df.residual"
#> [9] "xlevels" "call" "terms" "model"Código
plot(autompg$wt,autompg$mpg, pch=19, col=rgb(0.47,0.76,0.73,1),cex=1.5)
lines(autompg$wt,model$fitted.values)
plot(autompg$wt,autompg$mpg, pch=19, col=rgb(0.47,0.76,0.73,1),cex=1.5)
lines(autompg$wt,model$fitted.values)
abline(model$coefficients[1],model$coefficients[2],col="red")
model <- lm(mpg ~ wt + year, data = autompg)
summary(model) #>
#> Call:
#> lm(formula = mpg ~ wt + year, data = autompg)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -8.852 -2.292 -0.100 2.039 14.325
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.464e+01 4.023e+00 -3.638 0.000312 ***
#> wt -6.635e-03 2.149e-04 -30.881 < 2e-16 ***
#> year 7.614e-01 4.973e-02 15.312 < 2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.431 on 387 degrees of freedom
#> Multiple R-squared: 0.8082, Adjusted R-squared: 0.8072
#> F-statistic: 815.6 on 2 and 387 DF, p-value: < 2.2e-16Código
Código
import statsmodels.api as sm
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# Asumiendo que 'autompg' es tu DataFrame y ya ha sido procesado como en los pasos anteriores
X = autompg['wt']
y = autompg['mpg']
X = sm.add_constant(X) # Agregar constante para el intercepto
# Ajustar el modelo
model = sm.OLS(y, X).fit()
# Resumen del modelo
print(model.summary())#> OLS Regression Results
#> ==============================================================================
#> Dep. Variable: mpg R-squared: 0.692
#> Model: OLS Adj. R-squared: 0.691
#> Method: Least Squares F-statistic: 872.0
#> Date: sáb., 24 may. 2025 Prob (F-statistic): 2.81e-101
#> Time: 20:38:10 Log-Likelihood: -1125.1
#> No. Observations: 390 AIC: 2254.
#> Df Residuals: 388 BIC: 2262.
#> Df Model: 1
#> Covariance Type: nonrobust
#> ==============================================================================
#> coef std err t P>|t| [0.025 0.975]
#> ------------------------------------------------------------------------------
#> const 46.1984 0.802 57.595 0.000 44.621 47.775
#> wt -0.0076 0.000 -29.530 0.000 -0.008 -0.007
#> ==============================================================================
#> Omnibus: 41.559 Durbin-Watson: 0.812
#> Prob(Omnibus): 0.000 Jarque-Bera (JB): 59.570
#> Skew: 0.730 Prob(JB): 1.16e-13
#> Kurtosis: 4.239 Cond. No. 1.13e+04
#> ==============================================================================
#>
#> Notes:
#> [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
#> [2] The condition number is large, 1.13e+04. This might indicate that there are
#> strong multicollinearity or other numerical problems.Código
# Nombres de los atributos del modelo
print(model.params.index.tolist())#> ['const', 'wt']Código
# Crear la gráfica de dispersión
plt.figure(figsize=(10, 6))
plt.scatter(autompg['wt'], autompg['mpg'], color=(0.47, 0.76, 0.73, 1), s=60) # cex en R se traduce a s en plt.scatter
# Agregar la línea de ajuste del modelo
plt.plot(autompg['wt'], model.fittedvalues, color='black') # Líneas del modelo ajustado
# Etiquetas y título
plt.xlabel('Weight (wt)')
plt.ylabel('Miles per Gallon (mpg)')
plt.title('MPG vs Weight with Fitted Line')
# Mostrar la gráfica
plt.show()
Proposición 2.3 (Predicción) La predicción de una futura observación \(Y_0\), dados los valores de variables regresoras (covariables) \(\boldsymbol{x}_0\), es \(\widehat{Y}_0=\boldsymbol{x}_0^{\top}\widehat{\boldsymbol{\beta}}\). Se puede comprobar que esta predicción es una v.a. tal que \[ \widehat{Y}_0\sim N(\boldsymbol{x}_0^{\top}\boldsymbol{\beta}, \ \ \boldsymbol{x}_0^{\top}\left(X^{\top}X\right)^{-1}\boldsymbol{x}_0\sigma^2). \]
Proposición 2.4 (Error de Predicción) Consideramos \(Y_0=\boldsymbol{x}_0^{\top}\boldsymbol{\beta}+\epsilon_0\) con \(\epsilon_0 \sim N(0,\sigma^2)\) e independiente de los otros \(\epsilon_i\)’s. Entonces \[ Y_0-\widehat{Y}_0\ \sim N\left(0, \left[1+\boldsymbol{x}_0^{\top}\left(X^{\top}X\right)^{-1}\boldsymbol{x}_0\right]\sigma^2\right). \tag{2.4}\]
Notamos que la varianza tiene dos componentes. \(\sigma^2\) describe la variabilidad de \(Y\) alrededor de su media y \(\boldsymbol{x}_0^{\top}\left(X^{\top}X\right)^{-1}\boldsymbol{x}_0\sigma^2\) describe la incertidumbre de la media estimada para \(\boldsymbol{x}_0\).
2.6 Sobre prueba de hipótesis
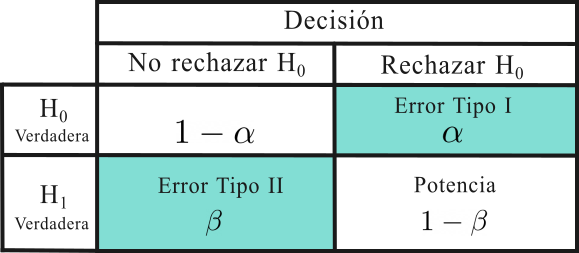
Un estadístico de prueba es un valor que se calcula en una prueba de hipótesis, para buscar evidencia en contra de la hipótesis nula.
Este estadístico tiene una distribución conocida bajo la hipótesis nula y busca medir el grado de concordancia entre una muestra de datos y ésta.
2.6.1 Modelo de Regresión Lineal Simple
El modelo es: \[ y=\beta_0+\beta_1 x+\epsilon, \qquad \text{con }\ \epsilon \sim N(0,\sigma^2). \] Para este modelo entonce \(k=1\) y \(p=2\), ya que se tiene un solo regresor pero dos coeficientes a estimar.
Los EMV coincide con el estimador de mínimos cuadrados y basado en \(n\) observaciones, es: \[ \widehat{\beta}_0=\overline{\boldsymbol{Y}}-\widehat{\beta}_1 \overline{\boldsymbol{x}}, \qquad \qquad \widehat{\beta}_1=\frac{S_{x y}}{S_{x x}}, \] donde \[ \begin{aligned} &S_{x x}=\sum_{i=1}^n x_i^2-\frac{\left(\sum_{i=1}^n x_i\right)^2}{n}=\sum_{i=1}^n\left(x_i-\overline{\boldsymbol{x}}\right)^2\\ &S_{x y}=\sum_{i=1}^n(x_i-\overline{\boldsymbol{x}})(y_i-\overline{\boldsymbol{Y}})=\sum_{i=1}^n y_i x_i-\frac{\left(\sum_{i=1}^n y_i\right)\left(\sum_{i=1}^n x_i\right)}{n}=\sum_{i=1}^n y_i\left(x_i-\overline{\boldsymbol{x}}\right)\\ \end{aligned} \] Los estimadores de \(\widehat{\beta}_0\) y \(\widehat{\beta}_1\) son insesgados y sus varianzas son:
\[ \begin{aligned} \operatorname{Var}\left(\widehat{\beta}_1\right) & =\frac{\sigma^2 \sum_{i=1}^n\left(x_i-\overline{\boldsymbol{x}}\right)^2}{S_{x x}^2} =\frac{\sigma^2}{S_{x x}}\\ \operatorname{Var}\left(\widehat{\beta}_0\right) & =\operatorname{Var}\left(\overline{\boldsymbol{Y}}-\widehat{\beta}_1 \overline{\boldsymbol{x}}\right) \\ & =\operatorname{Var}(\overline{\boldsymbol{Y}})+\overline{\boldsymbol{x}}^2 \operatorname{Var}\left(\widehat{\beta}_1\right)-2 \overline{\boldsymbol{x}} \operatorname{Cov}\left(\overline{\boldsymbol{Y}}, \widehat{\beta}_1\right)\\ & = \operatorname{Var}(\overline{\boldsymbol{Y}})+\overline{\boldsymbol{x}}^2 \operatorname{Var}\left(\widehat{\beta}_1\right) \\ & =\sigma^2\left(\frac{1}{n}+\frac{\overline{\boldsymbol{x}}^2}{S_{x x}}\right), \end{aligned} \] ya que \(\operatorname{Var}(\overline{\boldsymbol{Y}})=\sigma^2/n\) y por ?thm-Xb_ind_xi-xb, \(\operatorname{Cov}\left(\overline{\boldsymbol{Y}}, \widehat{\beta}_1\right)=0\).
A partir de la suma de cuadrado de los residuales, el estimador insesgado de \(\sigma^2\) (Teorema 2.2) es \[ s^2=\frac{SS_{\mathrm{Res}}}{n-2}. \]
Supongamos que se desea probar la hipótesis que la pendiente es igual a una constante, por ejemplo, a \(\beta^{\star}\). Las hipótesis correspondientes son \[ H_0: \beta_1=\beta_1^{\star} \qquad \text{Vs.} \qquad H_1: \beta_1 \neq \beta_1^{\star}, \] en donde se ha especificado una alternativa bilateral.
Como \(y_i\sim N\left(\beta_0+\beta_1 x_i, \sigma^2\right)\) entonces \(\widehat{\beta}_1 \sim N(\beta_1,\sigma^2 / S_{x x})\). Así, el estadístico
\[ Z_0 = \frac{\widehat{\beta}_1-\beta_1^{\star}}{\sqrt{\sigma^2 / S_{x x}}}, \] tiene distribucióm \(N(0,1)\) si es cierta la hipótesis nula \(H_0: \beta_1=\beta_1^{\star}\).
Si se conociera \(\sigma^2\), se podría usar \(Z_0\) para probar la hipótesis, pero comúnmente este no es el caso y se tiene que estimar. Usamos el estimador insesgado de \(\sigma^2\), \(SS_{\mathrm{Res}}/(n-2)\), para obtener un estadístico de prueba basado en la siguiente proposición.
Proposición 2.5 En general, para el modelo de Regresión:
- \((n-p)s^2/\sigma^2\sim \chi^2(n-p)\).
- \(s^2\perp \widehat{\boldsymbol{\beta}}\).
Entonces, usando ?thm-fgm_t, tenemos
\[ t_0=\frac{\widehat{\beta}_1-\beta_1^{\star}}{\sqrt{s^2 / S_{x x}}}=\frac{\frac{\widehat{\beta}_1-\beta_1^{\star}}{\sqrt{\sigma^2/S_{xx}}}}{\sqrt{\frac{(n-2)s^2/\sigma^2}{n-2}}}\sim t(n-2) \tag{2.5}\]
si es cierta la hipótesis nula \(H_0: \beta_1=\beta_1^{\star}\).
El procedimiento para realizar la prueba es calcular \(t_0\) basados en la observaciones y el ajuste, para comparar este valor observado Ecuación 2.5 con el los valores que en la distribución acumulan en la cola el \(\alpha \times 100\%\) de la distribución bajo \(H_0\). Es decir, mientras rechazamos la hipótesis nula si
\[ \left|t_0\right|>t(\alpha / 2; n-2) \] no tenemos evidencia para rechazar \(H_0\) en el caso contrario.
Es también deseable calcular en valor \(p\) (\(p\)-valor) que para esta prueba se define como \[ P(X\leq -t_0)+P(X\geq t_0)=2P(X>|t_0|), \] ya que la distribución \(t\) es simétrica alrededor del cero.
Como puede percibirse del Proposición 2.5, se puede realizar una prueba similar acerca de la ordenada al origen.
\[ H_0: \beta_0=\beta_0^{\star} \qquad \text{Vs.} \qquad H_1: \beta_0 \neq \beta_{0}^{\star}. \] En este caso se puede considerar el estadístico de prueba \[ t_0=\frac{\widehat{\beta}_0-\beta_{0}^{\star}}{\sqrt{s^2\left(\frac{1}{n}+\frac{\overline{x}^2}{S_{x x}}\right)}} \tag{2.6}\] La hipótesis nula \(H_0: \beta_0=\beta_{0}^{\star}\) se rechaza si \(\left|t_0\right|>t(\alpha / 2; n-2)\).
2.6.1.1 Pruebas de significancia de la regresión
Un caso especial muy importante de la hipótesis para \(\beta_1\) es el siguiente: \[ H_0: \beta_1=0 \qquad \text{Vs.} \qquad H_1: \beta_1 \neq 0 \]
Estas hipótesis se relacionan con la significancia de la regresión. El no rechazar \(H_0: \beta_1=0\) implica que no hay relación lineal entre \(x\) y \(y\).
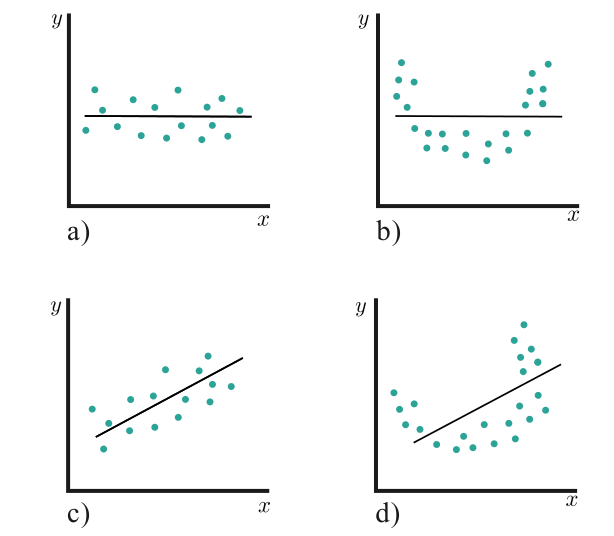
Esto se ilustra en la Figura 2.15 a) y b). En el primer caso \(x\) tiene muy poco valor para explicar la variación de \(y\) y que el mejor estimador para cualquier \(x\) es \(\widehat{y}=\overline{\boldsymbol{Y}}\). En el segundo caso, la verdadera relación entre \(x\) y \(y\) no es lineal. Por consiguiente, si no se rechaza \(H_0: \beta_1=0\), equivale a decir que no hay relación lineal entre \(y\) y \(x\).
También, si se rechaza \(H_0: \beta_1=0\), eso implica que \(x\) sí tiene valor para explicar la variabilidad de \(y\). Esto se ilustra en la figura c) y d). Sin embargo, rechazar \(H_0: \beta_1=0\) podría equivaler a que el modelo de línea recta es adecuado (c), o que aunque hay un efecto lineal de \(x\) se podrían obtener mejores resultados agregando términos polinomiales en \(x\) (d).
El procedimiento de prueba para \(H_0: \beta_1=0\) se puede establecer con dos métodos. El primero tan sólo usa el estadístico \(t\) en la Ecuación 2.5 con \(\beta_{0}^{\star}=0\) y el segundo es analizar la relevancia o significado de la regresión con el método de Análisis de varianza.
En el primer caso, el estadistico es simplemente \[ t_0=\frac{\widehat{\beta}_1}{\sqrt{s^2/S_{xx}}}, \] que bajo \(H_0\) se distribuye \(t(n-2)\).
Al denominador de estas pruebas se le denomina como la “error estándar del estimador” y se denota \(\text{se}(\widehat{\beta}_i)\) con \(i=1\) para este caso.
2.6.2 ANOVA unifactorial
ANOVA es el nombre corto para Análisis de Varianza (ANalysis Of VAriance). Al ANOVA unifactorial se le conoce también por su nombre en inglés “one-way ANOVA” Es un método estadístico que se utiliza para probar la hipótesis de que las medias de dos o más poblaciones son iguales.
Ejemplos de cuándo es posible que desee probar diferentes grupos:
- Un grupo de pacientes está probando tres terapias diferentes. Quieres ver si una terapia es mejor que las otras.
- Un fabricante tiene dos procesos diferentes para hacer bombillas. Quieren saber si un proceso es mejor que el otro.
- Los estudiantes de diferentes universidades toman el mismo examen. Quieres ver si una universidad supera a la otra.
El ANOVA implica comparar muestras aleatorias de varias poblaciones (grupos). A menudo, las muestras surgen de observar unidades experimentales a las que se les aplican diferentes tratamientos y nos referimos a las poblaciones como grupos de tratamiento.
Los tamaños de las muestras para los grupos pueden ser diferentes, digamos, \(n_i\) y asumimos que las muestras son todas independientes. Además, asumimos que cada población tiene la misma varianza y está distribuida normalmente. Asumiendo diferentes medias para cada grupo, tenemos el modelo \[ y_{i j}=\mu_i+\varepsilon_{i j}, \quad \varepsilon_{i j} \ \text { v.a.s i.i.d. }\ N\left(0, \sigma^2\right) \tag{2.7}\] donde hay \(g\) diferentes grupos, \(i=1,\ldots,g\) con \(n_i\) observaciones en el \(i-\)ésimo grupo, \(j=1,\ldots,n_i\).
El modelo Ecuación 2.7, que corresponde al ANOVA unifactorial se puede expresar como un modelo de regresión simple \[ \boldsymbol{Y}=X\boldsymbol{\beta}+\boldsymbol{\epsilon},\qquad \boldsymbol{\epsilon}\sim\ N_n\left(\boldsymbol{0},\ \sigma^2I_n\right) \] donde \(Y=(y_{1 1},y_{1 2},\ldots,y_{1 n_1},y_{2 1},\ldots,y_{g n_g})^{\top}\), \(\boldsymbol{\beta}=(\mu, \alpha_1,\alpha_2,\ldots, \alpha_g)^{\top}\) y \(X=[\boldsymbol{1}_n \boldsymbol{a}_{1} \boldsymbol{a}_{2} \cdots \boldsymbol{a}_{g}]\), donde \(\boldsymbol{a}_{j}\) es un vector de 0’s y 1’s, con unos para las observaciones que son del grupo \(j\). Así \(\mu_i\) en Ecuación 2.7 es igual a \(\mu_i=\mu+\alpha_i\), \(i=1,\ldots,n\).
En este sentido, la prueba de significancia: \[ H_0: \mu_1=\mu_2=\ldots=\mu_g \qquad \text{Vs.} \qquad H_1: \mu_s \ne \mu_t\quad \text{ para alguna }\ s\ne t \] equivale a
\[ H_0: \alpha_1=\alpha_2=\ldots=\alpha_g=0 \qquad \text{Vs.} \qquad H_1: \alpha_s \ne 0 \quad \text{ para alguna }\ s\ne t \]
En la práctica el modelo anterior es redundante ya que si se tienen \(g\) grupos solo se requieren \(g\) parámetros y no \(g+1\) como lo presenta el modelo anterior. De hecho \(\operatorname{rango}(X) = g\) aunque tenga las \(g+1\) columnas. Sin embargo, para presentar la relación entre la regresión y el ANOVA, este modelo es suficiente.
En el ANOVA unifactorial hay basicamente tres escenarios en los que se desea comparar las diferentes medias de poblaciones.
1. Hay un nuevo tratamiento y la variable de interés es el tiempo promedio de alta de los pacientes. Deseamos comparar el tiempo promedio del grupo de estudio y compararlo con el establecido tiempo esperado de alta \(\beta^{\star}\) ya conocido del tratamiento convencional.
En este caso los datos solo corresponden a datos de pacientes bajo el nuevo tratamiento, así que la variable \(\boldsymbol{x}\) es un vector de unos que indica que todos ellos son sometidos al nuevo tratamiento. En este caso nos interesa realizar la prueba \[ H_0: \mu=\mu^{\star} \qquad \text{Vs.} \qquad H_1: \mu \neq \mu^{\star}. \] Si se asume que \(\boldsymbol{Y}\) tiene distribución Normal, para realizar esta prueba se puede utilizar el estadístico: \[ t=\frac{ \frac{\overline{\boldsymbol{Y}}-\mu^{\star}}{\sqrt{\frac{\sigma^2}{n}}} }{ \sqrt{\frac{(n-1)s^2/\sigma^2}{(n-1)}} } =\frac{\overline{\boldsymbol{Y}}-\mu^{\star}}{\sqrt{\frac{s^2}{n}} }\sim t(n-1), \qquad \text{con }\ s^2=\frac{\sum(Y_i-\overline{\boldsymbol{Y}})^2}{n-1} \] usando ?thm-Xb_ind_xi-xb y ?thm-Ji_cuadrada_promMuestral.
2. Hay dos tratamientos, \(A\) y \(B\) que se quieren contrastar para ver si hay diferencia en los valores medios de \(Y\).
Si consideramos que \(Y\) tiene distribución Normal para \(A\) o \(B\) y la varianza es igual en ambos grupos, entonces lo que se quiere realizar es la prueba \[ H_0: \mu_A=\mu_B \qquad \text{Vs.} \qquad H_1: \mu_A \neq \mu_B. \] Si la muestra es pareada, el estadístico se define considerando \(W_i=Y_i-X_i\). Si \(W_i\) se distribuye Normal y bajo \(H_0\), \(W_i\sim N_n(0,\sigma^2), \ i=1,\ldots, n\), \[ t=\frac{\overline{W}}{\sqrt{\frac{s_W^2}{n}}}\sim t(n-1), \qquad \text{con }\ s_W^2=\frac{\sum(w_i-\overline{W})^2}{n-1} \] Cuando las muestras bajo uno y otro tratamiento (\(X_A\) y \(Y_B\)) son de tamaños \(n_1\) y \(n_2\), respectivamente, no son pareadas, son independientes, tienen la misma varianza y sus promedios tienen distribución Normal, entonces el estadístico que se puede utilizar es \[ t=\frac{\frac{\overline{\boldsymbol{Y}}_A-\overline{\boldsymbol{Y}}_B}{\sqrt{\sigma^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}}{\sqrt{\frac{\left[(n_1-1)S_A^2+(n_2-1)S_B^2\right]/\sigma^2}{n_1+n_2-2}}}=\frac{\overline{\boldsymbol{Y}}_A-\overline{\boldsymbol{Y}}_B}{\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\sqrt{\frac{(n_1-1)S_A^2+(n_2-1)S_B^2}{n_1+n_2-2}}}\sim t(n_1+n_2-2). \] Cuando \(n_1=n_2\), \[ t=\frac{\overline{\boldsymbol{Y}}_A-\overline{\boldsymbol{Y}}_B}{\sqrt{\frac{S_A^2+S_B^2}{n}}}\sim t\left(2(n-1)\right). \]
3. Hay \(g\) diferentes tratamientos y se quiere ver si hay diferencia en las medias de los resultados en alguno de ellos. Queremos hacer la prueba: \[ H_0: \mu_1=\mu_2=\ldots=\mu_g \qquad \text{Vs.} \qquad H_1: \mu_s \ne \mu_t\quad \text{ para alguna }\ s\ne t. \] Para extender los resultados anteriores, calculamos las estadísticas de la muestra en cada población. Obtenemos la media y varianza muestrales para el \(i-\)ésimo grupo: \[ \overline{\boldsymbol{Y}}_{i \cdot}=\frac{1}{n_i} \sum_{j=1}^{n_i} y_{i j} \quad \text{ y }\quad s_i^2=\frac{1}{n_i-1} \sum_{j=1}^{n_i}\left(y_{i j}-\overline{\boldsymbol{Y}}_{i \cdot}\right)^2 \] Como asumimos que los errores son independientes, Normales y con misma varianza, los estadísticos anteriores son todos independientes. Por facilidad, tipicamente se presentan en una tabla como:
Groupo Tamaño Media M. Varianza M. 1 \(n_1\) \(\overline{\boldsymbol{Y}}_1\). \(s_1^2\) 2 \(n_2\) \(\overline{\boldsymbol{Y}}_2\). \(s_2^2\) \(\vdots\) \(\vdots\) \(\vdots\) \(\vdots\) \(g\) \(n_g\) \(\overline{\boldsymbol{Y}}_g\). \(s_g^2\) Con tamaños de grupos diferentes, un estimador eficiente de \(\sigma^2\) es una promedio ponderado de las \(s_i's\). Los pesos son los grados de libertad asociados y este estimador \(s^2\) se denomina Error Cuadrático Medio (ECM o MSE o \(MS_{\mathrm{Res}}\) en inglés): \[ \begin{aligned} MS_{\mathrm{Res}} & := \frac{1}{\sum_{i=1}^g\left(n_i-1\right)}SS_{\text{Res}}=\frac{\left(n_1-1\right) s_1^2+\left(n_2-1\right) s_2^2+\cdots+\left(n_g-1\right) s_g^2}{\sum_{i=1}^g\left(n_i-1\right)} \\ & =\frac{1}{(n-g)} \sum_{i=1}^g \sum_{j=1}^{n_i}\left(y_{i j}-\overline{\boldsymbol{Y}}_i .\right)^2 \end{aligned} \] donde \(n=\sum_{i=1}^g n_i\) es el tamaño total de la muestra. Los grados de libertad del \(MS_{\mathrm{Res}}\) son \[ n-g=\sum_{i=1}^g\left(n_i-1\right). \] \(\overline{\boldsymbol{Y}}_{i}.\)’s son calculada de diferentes muestras así que son independientes. Además \[ \overline{\boldsymbol{Y}}_{i}. \sim N\left(\mu_i, \frac{\sigma^2}{n_i}\right). \] El segundo estimador de \(\sigma^2\) basado es menos intuitivo porque \(\overline{\boldsymbol{Y}}_{i}.\)s no tienen la misma varianza y aunque \(H_0\) es cierta, \(\{\overline{\boldsymbol{Y}}_{i}.\}\) no son una m.a. El estimador apropiado de \(\sigma^2\) es \[ MS_{\text{Trts}}:=\frac{1}{g-1}SS_{\text{Trts}}=\frac{1}{g-1}\sum_{i=1}^g n_i(\overline{\boldsymbol{Y}}_{i}.-\overline{\boldsymbol{Y}}..)^2, \] donde \[\overline{\boldsymbol{Y}}..=\frac{1}{n} \sum_{i=1}^g n_i \overline{\boldsymbol{Y}}_{i .}=\frac{1}{n} \sum_{i=1}^g \sum_{j=1}^{n_i} y_{i j}\ \ . \]
Por otro lado, \(\operatorname{SS}_{\text{Tot}} / \text{df}_{\text{Tot}}=s_y^2\), que es la variaza muestral del total de observaciones \(n\) sin referencia a tratamientos/grupos. Los grados de libertad de la sumas cuadradas para los grupos (tratamientos) y error se pueden sumar para obtener los grados de libertad de las sumas cuadradas totales, _{}.
Los estimadores, con sus grados de libertad se resumen en la siguiente tabla:
Source df SS MS F Tratamientos \(g-1\) \(\sum_{i=1}^g n_i\left(\overline{\boldsymbol{Y}}_{i}.-\overline{\boldsymbol{Y}}..\right)^2\) \(SS_{\text{Trts}} /(g-1)\) \(MS_{\text{Trts}}/MS_{\text{Res}}\) Error / Residual \(n-g\) \(\sum_{i=1}^g \sum_{j=1}^{n_i}\left(y_{i j}-\overline{\boldsymbol{Y}}_{i}.\right)^2\) \(SS_{\mathrm{Res}} /(n-g)\) Total \(n-1\) \(\sum_{i=1}^g \sum_{j=1}^{n_i}\left(y_{i j}-\overline{\boldsymbol{Y}}..\right)^2\)
Se puede mostrar que \(MS_{\text{Trts}} \perp MS_{\mathrm{Res}}\) y \[ MS_{\text{Trts}}\sim \chi^2(g-1) \quad \text{ y }\quad MS_{\mathrm{Res}}\sim \chi^2(n-g) \] Entonces, bajo \(H_0\),
\[ F=\frac{MS_{\text{Trts}}}{MS_{\text{Res}}}\sim F(g-1,n-g). \]
Antes de que una comparación de medias que hemos visto, se debe verificar si es adecuado considerar que las las varianzas son iguales. Una de las pruebas que se puede realizar es la prueba de Levene.
Prueba de Levene
Una de las pruebas que se puede realizar para evaluar si hay alguna evidencia de que las varianzas entre grupos/poblaciones es diferente es la prueba de Levene. Si tenemos \(g\) grupos queremos realizar la prueba: \[ H_0: \sigma_1=\sigma_2=\ldots=\sigma_g \qquad \text{Vs.} \qquad H_1: \sigma_i \ne \sigma_j\quad \text{ para alguna }\ i\ne j. \tag{2.8}\]
En caso de tener dos tratamientos / poblaciones: \(X_1, X_2, \ldots, X_n\) m.a. de tamaño \(n\) y \(Y_1, Y_2, \ldots, Y_m\) de tamaño \(m\). Ambas con distribuciones Normales con media \(\mu_X\) y \(\mu_Y\) y varianzas \(\sigma_X^2\) y \(\sigma_Y^2\), repectivamente. Recordemos que para los datos de cada población: \[ \frac{(n-1) s_X^2}{\sigma_X^2}\sim \chi^2(n-1)\quad \text { and }\quad \frac{(m-1) s_Y^2}{\sigma_Y^2}\sim \chi^2(m-1) \]
Como además son independientes, \[ F=\frac{\frac{(n-1) s_X^2}{\sigma_x^2} /(n-1)}{\frac{(m-1) s_Y^2}{\sigma_Y^2} /(m-1)}=\frac{s_X^2}{s_Y^2} \cdot \frac{\sigma_Y^2}{\sigma_X^2} \sim F(n-1,m-1). \] Además bajo \(H_0: \sigma^2_X=\sigma^2_Y\), \[ F=\frac{s_X^2}{s_Y^2} \sim F(n-1,m-1). \]
En caso de tener \(g\) tratamientos / poblaciones la prueba de Levene para Ecuación 2.8 tenemos una m.a. \(\{Y_{ij}\}\) con muestra de tamaño total \(n\) dividida en \(g\) poblaciones. El estadístico de prueba de Levene se define como:
\[ W=\frac{(n-g)}{(g-1)} \frac{\sum_{i=1}^g n_i\left(\overline{Z}_{i .}-\overline{Z}_{. .}\right)^2}{\sum_{i=1}^g \sum_{j=1}^{n_i}\left(Z_{i j}-\overline{Z}_{i .}\right)^2}, \] dónde \(\boldsymbol{Z}_{i j}\) puede tener una de las siguientes tres definiciones:
- \(Z_{i j}=\left|Y_{i j}-\overline{\boldsymbol{Y}}_i\right|\),
- \(Z_{i j}=\left|Y_{i j}-\operatorname{med}(\boldsymbol{Y}_i)\right|\), donde \(\operatorname{med}(\boldsymbol{Y}_i)\) es el mediana del \(i-\)ésimo grupo,
- \(Z_{i j}=\left|Y_{i j}-\overline{\boldsymbol{Y}}_i^{\prime}\right|\), donde \(\overline{\boldsymbol{Y}}_i^{\prime}\) es el \(10 \%\) media recortada (trimmed mean)del \(i-\)ésimo grupo.
La prueba de Levene rechaza la hipótesis nula si
\[ W > F\,(\,1-\alpha\ ;\ g-1,\ n-g\,) \] donde \(F\,(\,1-\alpha\ ;\ g-1,\ n-g\,)\) es el \((1-\alpha)\times 100\%\) percentil de la distribución \(F\) con \(g-1\) y \(n-g\) grados de libertad.
Ejemplo: ANOVA unifactorial
La siguiente tabla presenta datos de Koopmans (1987, p. 409) sobre las edades a las que se cometieron suicidios en Albuquerque durante 1978. Las edades están listadas por grupo étnico. Se asume que las observaciones en cada grupo son una muestra aleatoria de alguna población. Aunque no está claro qué serían estas poblaciones, procedemos a examinar los datos.
Edades de Suicidio (Christensen, R., 1996)
| Blancos No-Latinos | Latinos | Nativos Americanos |
|---|---|---|
| 21 31 28 52 | 50 27 45 | 26 23 |
| 55 31 24 27 | 31 22 57 | 17 25 |
| 42 32 53 76 | 29 20 22 | 24 23 |
| 25 43 66 44 | 21 51 48 | 22 22 |
| 48 57 90 35 | 27 60 48 | 16 |
| 22 42 27 32 | 34 15 14 | 21 |
| 42 34 48 26 | 76 19 52 | 36 |
| 53 39 47 51 | 35 24 29 | 18 |
| 21 24 49 19 | 55 24 21 | 48 |
| 21 79 53 27 | 24 18 28 | 20 |
| 31 46 62 58 | 68 43 17 | 35 |
| 38 |
Código
library(ggplot2)
dat <- read.csv("data/suicidio.csv",head = TRUE)
# Box plot by group with jitter
ggplot(dat, aes(x = Grupo, y = Edad, colour = Grupo)) +
geom_boxplot(outlier.shape = NA) +
geom_jitter()
De la Figura 2.16 podemos ver fácilmente que las edades para los nativos americanos parecen ser tanto más bajas como menos variables que para los otros grupos. Las edades para latinos parecen ser un poco más bajas que para los caucásicos no latinos.
Prueba de hipótesis para varianzas \[ H_0: \sigma_1=\sigma_2=\sigma_3 \qquad \text{Vs.} \qquad H_1: \sigma_i \ne \sigma_j\quad \text{ para alguna }\ i\ne j. \] Consideramos \(Z_{i j}=\left|Y_{i j}-\overline{\boldsymbol{Y}}_i\right|\), y realizamos la prueba. Reportamos el p-valor.
Show the code
dat <- read.csv("data/suicidio.csv",head = TRUE)
ZB <- dat[dat[,'Grupo']=='B','Edad']-mean(dat[dat[,'Grupo']=='B','Edad'])
ZL <- dat[dat[,'Grupo']=='L','Edad']-mean(dat[dat[,'Grupo']=='L','Edad'])
ZN <- dat[dat[,'Grupo']=='N','Edad']-mean(dat[dat[,'Grupo']=='N','Edad'])
n <- dim(dat)[1]
k <- 3
num <- (n-k)*sum((c(mean(ZB),mean(ZL),mean(ZN))-mean(c(ZB,ZL,ZN)))^2*c(length(ZB),length(ZL),length(ZN)))
den <- (k-1)*(sum((ZB-mean(ZB))^2)+sum((ZL-mean(ZL))^2)+sum((ZN-mean(ZN))^2))
w <- num/den
cat("w = ",w)#> w = 1.378012e-30#> p-valor = 1Show the code
Como hay casi nula evidencia en contra de \(H_0\), procedemos a realizar el ANOVA para probar si hay diferencia significativa entre edades de cada grupo.
Código
YB <- dat[dat[,'Grupo']=='B','Edad']
YL <- dat[dat[,'Grupo']=='L','Edad']
YN <- dat[dat[,'Grupo']=='N','Edad']
SSTrts <- sum((c(mean(YB),mean(YL),mean(YN))-mean(dat[,'Edad']))^2*c(length(ZB),length(ZL),length(ZN)))
SSE <- sum((YB-mean(YB))^2)+sum((YL-mean(YL))^2)+sum((YN-mean(YN))^2)
f <- (SSTrts/(k-1))/(SSE/(n-k))
cat("Estadistico f =",f)#> Estadistico f = 6.541203#> p-valor = 0.002226426Código
####### Ahora usamos aov de R
str(dat)#> 'data.frame': 93 obs. of 12 variables:
#> $ Edad : int 21 55 42 25 48 22 42 53 21 21 ...
#> $ Grupo : chr "B" "B" "B" "B" ...
#> $ ybi. : num 41.7 41.7 41.7 41.7 41.7 ...
#> $ Zij : num -20.659 13.341 0.341 -16.659 6.341 ...
#> $ Zbi. : num 2.58e-15 2.58e-15 2.58e-15 2.58e-15 2.58e-15 ...
#> $ X.Zij.Zbi...2 : num 426.798 177.98 0.116 277.525 40.207 ...
#> $ Zbi..1 : num 2.58e-15 -3.34e-15 2.37e-16 NA NA ...
#> $ Zb.. : int 0 0 0 NA NA NA NA NA NA NA ...
#> $ X : chr "" "" "" "" ...
#> $ ni : chr "44" "34" "15" "" ...
#> $ n : chr "93" "" "" "" ...
#> $ ni..Zbi..Zb....2: num 2.94e-28 3.80e-28 8.41e-31 NA 6.07e-26 ...#> Df Sum Sq Mean Sq F value Pr(>F)
#> Grupo 2 3202 1601.0 6.541 0.00223 **
#> Residuals 90 22029 244.8
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Entonces a un nivel de significancia \(\alpha\) menor a 0.2%, no rechazamos \(H_0\) pero a un nivel de significancia mayor a 0.223% tenemos la suficiente evidencia para rechazar \(H_0\).
2.6.3 Modelo de Regresión Lineal (Múltiple)
2.6.3.1 Pruebas de significancia de la regresión
La prueba de la significancia de la regresión es para determinar si hay una relación lineal entre la respuesta \(Y\) y cualquiera de las variables regresoras \(x_1, x_2, \ldots, x_k\): \[ H_0: \beta_1=\beta_2=\cdots=\beta_k=0 \qquad \text{Vs.} \qquad H_1: \beta_j \neq 0 \text { para alguna } j . \tag{2.9}\]
Recordamos que \(p\) es el número de variables, pero el número de covariables es \(k = p-1\).
El procedimiento de prueba es una generalización del caso de regresión lineal simple. Para esto, realizamos las siguientes definiciones.
Definición 2.4 (Sumas de cuadrados (SS’s)) La Suma de cuadrados Total, Regresion y Residuales, se definen, respectivamente, como \[ \begin{aligned} SS_{\mathrm{T}} &= \sum_{i=1}^n\left(Y_i-\overline{\boldsymbol{Y}}\right)^2,\\ SS_{\mathrm{R}} &= \sum_{i=1}^n\left(\widehat{Y}_i-\overline{\boldsymbol{Y}}\right)^2,\\ SS_{\mathrm{Res}} &= \sum_{i=1}^n\left(Y_i-\widehat{Y}_i\right)^2. \end{aligned} \]
Para extender las pruebas anteriores, descomponemos el error total como la suma de los errores de Regresion y Residuales.
Teorema 2.3 (Partición de la variabilidad total) La suma total de cuadrados \(SS_{\mathrm{T}}\) se divide en una suma de cuadrados debidos a la regresión, \(SS_{\mathrm{R}}\), y a una suma de cuadrados de residuales, \(SS_{\mathrm{Res}}\). Así, \[ SS_{\mathrm{T}}=SS_{\mathrm{R}}+SS_{\mathrm{Res}}. \]
Teorema 2.4 (Distribución de \(SS_{\mathrm{R}}\)) \[ SS_{\mathrm{R}} = \sum_{i=1}^n\left(\widehat{Y}_i-\overline{\boldsymbol{Y}}\right)^2 \sim \chi^2(p-1, \lambda)=\chi^2(k, \lambda), \] donde el parámetro de no centralidad es \[ \lambda=\frac{1}{2\sigma^2} \boldsymbol{\beta}_{\mathrm{R}}^{\top}\left[X_{\mathrm{C}}^{\top} X_{\mathrm{C}}\right] \boldsymbol{\beta}_{\mathrm{R}} \tag{2.10}\] con \(X_{\mathrm{C}}\) la matriz centrada de los regresores: \[ \begin{aligned} &X_{\mathrm{C}}=\left[\begin{array}{cccc} x_{11}-\overline{\boldsymbol{x}}_1 & x_{12}-\overline{\boldsymbol{x}}_2 & \cdots & x_{1 k}-\overline{\boldsymbol{x}}_k \\ x_{21}-\overline{\boldsymbol{x}}_1 & x_{22}-\overline{\boldsymbol{x}}_2 & \cdots & x_{2 k}-\overline{\boldsymbol{x}}_k \\ \vdots & \vdots &\ddots & \vdots \\ x_{n 1}-\overline{\boldsymbol{x}}_1 & x_{n 2}-\overline{\boldsymbol{x}}_2 & \cdots & x_{n k}-\overline{\boldsymbol{x}}_k \end{array}\right] \end{aligned} \tag{2.11}\] (donde \(\overline{\boldsymbol{x}}_i\) el promedio de los valores para la \(i-\)ésima covariable) y \(\boldsymbol{\beta}_{\mathrm{R}}\) son los valores de beta que excluye el de la ordenada al origen.
Teorema 2.5 (Media de \(MS_{\mathrm{R}}\)) \[ E\left(M S_{\mathrm{R}}\right)=E\left(\frac{S S_{\mathrm{R}}}{p-1}\right)=\sigma^2+\frac{\boldsymbol{\beta}_{\mathrm{R}}^{\top} X_{\mathrm{C}}^{\top} X_{\mathrm{C}} \boldsymbol{\beta}_{\mathrm{R}}}{p-1}. \]
2.6.3.2 Distribución de \(SS_{\mathrm{Res}}\)
\[ \begin{aligned} &SS_{\mathrm{Res}}=\sum_{i=1}^n\left(Y_i-\widehat{Y}_i\right)^2 \sim \chi^2(n-p). \end{aligned} \]
2.6.3.3 Media de \(MS_{\mathrm{Res}}\)
\[ E\left(M S_{\mathrm{Res}}\right)=E\left(\frac{S S_{\mathrm{Res}}}{n-p}\right)=\sigma^2. \]
2.6.3.4 Prueba F global o general
\(SS_{\mathrm{Res}}\) \[ \frac{M S_{\mathrm{R}}}{M S_{\mathrm{Res}}} \sim F\,(\, p-1,\ n-p,\ \lambda), \] donde el parámetro de no centralidad es igual al del Teorema 2.4.
En el simple caso de regresión lineal simple, tenemos \(\beta_{\mathrm{R}}=\beta_1\) y \[ X_{\mathrm{C}}^{\top} X_{\mathrm{C}}=\sum_{i=1}^n\left(x_i-\overline{\boldsymbol{x}}\right)^2 \] Entonces \[ \frac{M S_{\mathrm{R}}}{M S_{\mathrm{Res}}} \sim F\,(\, 1,\ n-2,\ \lambda) \] donde \(\lambda=\beta_1^2 \sum_{i=1}^n\left(x_i-\overline{\boldsymbol{x}}\right)^2/(2\sigma^2)\), con \(\boldsymbol{x}=x_1,\ldots,x_n\) son las observaciones de la única covariable.
Para realizar la prueba de significancia de la regresión (Ecuación 2.9) utilizamos justamente Teorema 2.4 para calcular el estadístico \(F_0\) y calcular su p-valor para saber cuanta evidencia se tiene contra \(H_0\).
Similar al ANOVA, los programas comúnmente reportan la prueba de significancia de la regresión en un arreglo como el siguiente:
| Source | df | Sum of Squares | Mean Square | F |
|---|---|---|---|---|
| Regression | \(k=p-1\) | \(SS_{\mathrm{R}}\) | \(MS_{\text{R}}\) | \(MS_{\text{R}}/MS_{\mathrm{Res}}\) |
| Residual | \(n-k-1=n-p\) | \(SS_{\mathrm{Res}}\) | \(MS_{\text{Res}}\) | |
| Total | \(n-1\) | \(SS_{\mathrm{T}}\) |
2.6.3.5 \(R^2\) y \(R^2\) ajustada
Otras dos maneras de evaluar la adecuación general del modelo son los estadísticos \(R^2\) y \(R^2\) ajustada; esta última se representa por \(R_{\text {Adj. }}^2\). Estos resultados son también populares en los programas que realizan el ajuste y se reportan en los resúmenes.
Definición 2.5 (Coeficiente de determinación) \(R^2\), también denominado como coeficiente de determinación, es un estadístico que mide la proporción de la varianza en \(y\) que se puede explicar por las covariables. Formalmente se define como \[ R^2=\frac{SS_{\mathrm{R}}}{SS_{\mathrm{T}}}=1-\frac{SS_{\mathrm{Res}}}{SS_{\mathrm{T}}}. \]
En otras palabras, \(R^2\) muestra que tan bien el modelo de regresión ajusta los datos (bondad de ajuste).
En general valores de \(R^2\) cercanos a uno son deseables, pero \(R^2\) aumenta siempre, cuando se agrega un regresor al modelo, independientemente del valor de la contribución de esa variable. En consecuencia, es difícil juzgar si un aumento de \(R^2\) dice en realidad algo importante.
Definición 2.6 (\(R^2\) ajustada) En la práctica es muchas veces preferible usar el estadístico \(R^2\) ajustada, que se define como: \[ R_{\mathrm{Adj}}^2=1-\frac{S S_{\mathrm{Res}} /(n-p)}{S S_{\mathrm{T}} /(n-1)}. \]
Como \(S S_{\text {Res }} /(n-p)\) es el cuadrado medio de residuales y \(S S_{\mathrm{T}} /(n-1)\) es constante, independientemente de cuántas variables hay en el modelo, \(R_{\text {Adj }}^2\) sólo aumentará al agregar una variable al modelo si esa adición reduce el cuadrado medio residual.
En los capítulos posteriores, al describir la construcción de modelos y la selección de variables será útil contar con un procedimiento que pueda evitar un sobreajuste del modelo, esto es, agregar términos que son innecesarios. La \(R^2\) ajustada penaliza la adición de términos que no son útiles, además que es ventajoso para evaluar y comparar los modelos posibles de regresión.
2.6.4 Prueba de submodelos
Supongamos que no rechazamos la hipótesis estadística anterior. Esto no significa que algunos de las variables no sean significativas. Queremos contrastar algún modelo reducido o submodelo, con el modelo completo \(\boldsymbol{Y}=X\boldsymbol{\beta}+\boldsymbol{\epsilon}\). Es decir, queremos ver si podemos rechazar la hipótesis nula en la que el modelo completo es adecuado, en favor de la alternantiva en donde el modelo reducido es tan bueno como el completo.
2.6.5 Prueba \(F\)
Denotamos al modelo reducido como \[ \boldsymbol{Y}=X_0 \boldsymbol{\gamma}+\boldsymbol{\varepsilon}, \quad \boldsymbol{\varepsilon} \sim N_n\left(0, \sigma^2 I\right), \quad \mathcal{C}\left(X_0\right) \subset \mathcal{C}(X). \]
Consideramos el modelo completo de regresión lineal: \[ \boldsymbol{Y}=X \boldsymbol{\beta} +\boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim N_n\left(\boldsymbol{0}, \sigma^2 I_n\right) \] que se mantiene para algunos valores de \(\boldsymbol{\beta}\) and \(\sigma^2\).
Bajo el modelo reducido: \[ \boldsymbol{Y} =X_0 \boldsymbol{\gamma}+\boldsymbol{\varepsilon}, \quad \boldsymbol{\varepsilon}\sim N_n\left(\boldsymbol{0}, \sigma^2 I_n\right), \quad \mathcal{C}\left(X_0\right) \subset \mathcal{C}(X). \] Aquí denotamos el rango de una matriz \(A\) como \(\operatorname{ran}(A)\).
- Si el modelo completo es verdadero,
\[ F_0=\frac{\boldsymbol{Y}^{\top}\left(P-P_0\right) \boldsymbol{Y} / \operatorname{ran}\left(P-P_0\right)}{\boldsymbol{Y}^{\top}(I_n-P) \boldsymbol{Y} / \operatorname{ran}(I_n-P)} \sim F\left(\operatorname{ran}\left(P-P_0\right),\ \operatorname{ran}(I_n-P), \ \frac{1}{2 \sigma^2}\beta^{\top} X^{\top}\left(P-P_0\right) X \beta \right). \]
- Si el modelo reducido es verdadero,
\[ F_0=\frac{\boldsymbol{Y}^{\top}\left(P-P_0\right) \boldsymbol{Y} / \operatorname{ran}\left(P-P_0\right)}{\boldsymbol{Y}^{\top}(I_n-P) \boldsymbol{Y} / \operatorname{ran}(I_n-P)} \sim F\left(\,\operatorname{ran}\left(P-P_0\right),\ \operatorname{ran}(I_n-P),\ 0\right) \]
Cuando el modelo completo es verdadero, esta distribución es cierta si y sólo si el modelo reducido es cierto.
Como \[ \begin{align} \boldsymbol{Y}^{\top}\left(P-P_0\right) \boldsymbol{Y} &=\boldsymbol{Y}^{\top}\left[(I_n-P_0)-(I_n-P)\right] \boldsymbol{Y}\\ &= \boldsymbol{Y}^{\top}\left(I_n-P_0\right)\boldsymbol{Y}-\boldsymbol{Y}^{\top}\left(I_n-P\right) \boldsymbol{Y}\\ &=SS_{\mathrm{Res},\ \text{Mod Reducido}}-SS_{\mathrm{Res},\ \text{Mod Completo}}\ \ , \end{align} \] entonces \(F_0\) del teorema anterior, se puede expresar como \[ F_0=\frac{\left[SS_{\mathrm{Res},\ \text{Mod Reducido}}-SS_{\mathrm{Res},\ \text{Mod Completo}}\right] / \operatorname{ran}\left(P-P_0\right)}{SS_{\mathrm{Res},\ \text{Mod Completo}} / \operatorname{ran}(I_n-P)}. \]
2.6.6 Prueba de Razón de Verosimilitudes
Todas las pruebas anteriores se basan fuertemente en el supuesto de que los errores son gausianos, independientes y su varianza es constante. Sin embargo hay pruebas estadísticas, que aunque se basen en alguna distribución o propiedad limite, se pueden aplicar en una variedad más amplia de modelos. Tal es el caso de la prueba de razones de verosimilitudes.
Recordamos que el estadístico derivado de la razón de verosimilitudes, para un modelo parametrizado con \(\boldsymbol{\theta}\) y para las hipótesis
\[ H_0: \boldsymbol{\theta} \in \Theta_0 \quad \quad \text{Vs. } \quad \quad H_1:\boldsymbol{\theta}\in \Theta \] con \(\Theta_0\subset \Theta\), es \[ \Lambda =-2\left[\log L_{\Theta_0}(\boldsymbol{\widehat\theta}) -\log L_{\Theta}(\boldsymbol{\widehat \theta})\right], \] donde \(L_{\Theta_0}(\boldsymbol{\hat\theta})\) y \(L_{\Theta}(\boldsymbol{\widehat \theta})\) son las verosimilitudes evaluadas en los EMV’s restringidos a \(\Theta_0\) y \(\Theta\), respectivamente. Dado que \(\Theta_0\subset \Theta\) entonces la primera versomilitud es menor o igual que la segunda y entonces \(\Lambda\geq 0\).
Por otro lado, bajo condiciones de regularidad, que incluye que el soporte de los modelos no dependan del parámetro y que los EMV bajo ambos modelos estén en el interior de los espacios paramétricos, \[ \Lambda \sim \chi^2(\lambda) \tag{2.14}\] con \(\lambda\) la diferencia del número de parámetros entre los dos modelos.
La hipótesis nula considera el modelo restringido mientras que la alternativa señala el modelo completo.
A continuación presentamos un boquejo del resultado en Ecuación 2.14. Primero denotamos \(\widehat{\boldsymbol{\theta}}\) el EMV en \(\Theta\) y \(\widehat{\boldsymbol{\theta}}^{\star}\) el EMV en el espacio \(\Theta_0\).
En la prueba de hipótesis de submodelos, podemos asumir, sin pérdida de generalidad, que los vectores de \(\Theta_0\) son de la misma longitud que los de \(\Theta\) (ambos de longitud \(p\)), pero los úultimos \(p-q\) elementos de \(\Theta_0\) son 0. Entonces el EMV considerando el modelo completo es \[ \widehat{\boldsymbol{\theta}}=(\widehat{\theta}_1,\widehat{\theta}_2,\ldots,\widehat{\theta}_q,\widehat{\theta}_{q+1}, \ldots, \widehat{\theta}_p), \] y bajo \(H_0\) el EMV es \[ \widehat{\boldsymbol{\theta}^{\star}}=(\widehat{\theta}_1^{\star},\widehat{\theta}_2^{\star},\ldots,\widehat{\theta}_q^{\star}, 0, \dots,0). \]
Como el EMV es consistente, tenemos que \(\widehat{\theta}_i \rightarrow \theta_i\) y \(\widehat{\theta}_i^{\star} \rightarrow \theta_i\) para \(1 \leq i \leq q\), y \(\widehat{\theta}_i^{\star} \rightarrow 0\) para \(q+1 \leq i \leq p\).
Ahora consideramos la expansión de Taylor hasta el segundo orden, de la log verosimilitud \(\ell=\log L\) de \(\widehat{\theta}^{\star}\) alrededor de \(\widehat{\theta}\): \[ \begin{aligned} \ell(\widehat{\boldsymbol{\theta}^{\star}}) & \approx \ell(\widehat{\boldsymbol{\theta}}) +\sum_{i=1}^p\left(\widehat{\theta}_i-\widehat{\theta}_i^{\star}\right)\left(\left.\frac{\partial \ell}{\partial \theta_i} \right|_{\widehat{\boldsymbol{\theta}}}\right) +\frac{1}{2} \sum_{i=1}^p \sum_{j=1}^p \left(\widehat{\theta}_i - \widehat{\theta}_i^{\star}\right) \left(\left.\frac{\partial^2 \ell}{\partial \theta_i \partial \theta_j}\right|_{\widehat{\boldsymbol{\theta}}}\right)\left(\widehat{\theta}_j-\widehat{\theta}_j^{\star}\right) \\ & =\ell(\widehat{\boldsymbol{\theta}}) +\frac{1}{2} \sum_{i=1}^p \sum_{j=1}^p\left(\widehat{\theta}_i - \widehat{\theta}_i^{\star}\right) \left(\left.\frac{\partial^2 \ell}{\partial \theta_i \partial \theta_j}\right|_{\widehat{\boldsymbol{\theta}}}\right)\left(\widehat{\theta}_j-\widehat{\theta}_j^{\star}\right), \end{aligned} \] ya que bajo el supuesto que el EMV se alcanza en un punto interior de \(\Theta\), las primeras derivadas parciales de primer orden se anulan.
Ahora supongamos que la matriz Hessiana de \(\ell\) es diagonal. Esto se puede lograr diagonalizando y extendiendo los cálculos, pero hacemos este supuesto para mantener esta descripción breve. Así que ahroa suponemos que \[ \left.\frac{\partial^2 \ell}{\partial \theta_i \partial \theta_j}\right|_{\widehat{\boldsymbol{\theta}}}=0 \qquad \text{para }\quad i\ne j. \] Entonces \[ \ell(\widehat{\boldsymbol{\theta}})-\ell(\widehat{\boldsymbol{\theta}^{\star}}) \approx-\frac{1}{2} \sum_{i=1}^p\left(\widehat{\theta}_i-\widehat{\theta}_i^{\star}\right)^2 \left(\left.\frac{\partial^2 \ell}{\partial \theta_i \partial \theta_i}\right|_{\widehat{\boldsymbol{\theta}}}\right) \] Si y sólo si \[ 2\left[\ell(\widehat{\boldsymbol{\theta}})-\ell(\widehat{\boldsymbol{\theta}^{\star}})\right] \approx-\sum_{i=1}^q\left(\widehat{\theta}_i-\widehat{\theta^{\star}}_i\right)^2 \left(\left.\frac{\partial^2 \ell}{\partial \theta_i \partial \theta_i}\right|_{\widehat{\boldsymbol{\theta}}}\right) -\sum_{i=q+1}^p \widehat{\theta}_i^2 \left(\left.\frac{\partial^2 \ell}{\partial \theta_i \partial \theta_i}\right|_{\widehat{\boldsymbol{\theta}}}\right) \tag{2.15}\] Nosotros ya sabemos que una de las propiedades de los EMV es \[ \widehat{\boldsymbol{\theta}}\xrightarrow[]{d} N(\boldsymbol{\theta},\mathcal{I}_n(\boldsymbol{\theta})^{-1} ) \] donde la función de información de Fisher es la matriz, \(n\times n\), positiva semidefinida donde la entrada \(i,j\) es \[ \left[\mathcal{I}_n(\boldsymbol{\theta})\right]_{i, j}=\mathrm{E}\left[\left.\left(\frac{\partial}{\partial \theta_i} \ell (\boldsymbol{\theta};\boldsymbol{X})\right)\left(\frac{\partial}{\partial \theta_j} \ell(\boldsymbol{\theta};\boldsymbol{X})\right) \right|_ \theta\right]=-\mathrm{E}\left[\left.\frac{\partial^2}{\partial \theta_i \partial \theta_j} \ell(\boldsymbol{\theta} ;\boldsymbol{X}) \right|_\theta\right], \] bajo condiciones de regularidad.
Considerando que \(\mathcal{I}_n(\theta)\) es la función de información de Fisher correspondiente a \(\boldsymbol{X}\) con \(n\) elementos y \(\mathcal{I}(\theta)\) es la correspondiente para una sola \(X\), tenemos que
\[ \mathcal{I}(\theta)=\sum_{i=1}^n \mathcal{I}_1(\theta)= n \mathcal{I}_1(\boldsymbol{\theta}) \tag{2.16}\] Entonces, \[ \widehat{\boldsymbol{\theta}}\xrightarrow[]{d} N\left(\boldsymbol{\theta},\frac{1}{n}\mathcal{I}_1(\boldsymbol{\theta})^{-1} \right) \tag{2.17}\] Aqui hacemos otros dos saltos y usamos \[ \frac{\partial^2\ell(\boldsymbol{\theta} ;\boldsymbol{X})}{\partial \theta_i \partial \theta_i} \approx-[\mathcal{I}_n(\boldsymbol{\theta})]_{ii} \tag{2.18}\] así \[ \begin{aligned} \widehat{\theta}_i & \approx \mathcal{N}\left(\theta_i\, ,\ -\frac{1}{n\ [\mathcal{I}_1]_{i i}}\right),\quad \text{y} \\ \widehat{\theta^{\star}}_i & \approx \mathcal{N}\left(\theta_i\, ,\ -\frac{1}{n\ [\mathcal{I}_1]_{i i}}\right)\qquad 1 \leq i \leq q, \\ \widehat{\theta^{\star}}_i & = 0 \qquad \qquad \qquad \qquad \quad q+1 \leq i \leq n. \end{aligned} \] Como la convergencia de los estimadores bajor el modelo reducido y completo es hacia los mismos valores para \(1 \leq i \leq q\), es solo la segunda suma del lado derecho de Ecuación 2.15 que define la distribución de la diferencia entre los modelos completo y reducido.
Por un lado, de Ecuación 2.17, tenemos que \[ \frac{\widehat{\theta}_i - \theta_i}{\sqrt{\frac{1}{n[\mathcal{I}_1]_{ii}(\theta)}}} = (\widehat{\theta}_i - \theta_i)\sqrt{[\mathcal{I}_n]_{ii}} \approx \mathcal{N}(0, 1) \] Ahora, bajo \(H_0\), \(\theta_i=0\) para \(q+1\leq i\leq n\), así que cuando \(H_0\) es cierta, \[ \widehat{\theta}_i^2 [\mathcal{I}_n]_{ii} \approx \mathcal{N}(0, 1) \] Finalmente, tenemos que \[ -2\left[\ell(\widehat{\boldsymbol{\theta}})-\ell(\widehat{\boldsymbol{\theta}^{\star}})\right] \approx \sum_{i=q+1}^p \widehat{\theta}_i^2 \left(\left.\frac{\partial^2 \ell}{\partial \theta_i \partial \theta_i}\right|_{\widehat{\boldsymbol{\theta}}}\right) \approx \chi^2(p-q). \] Por mucho esto no es una demostración, sino solo la exposición de ideas detrás de este resultado.
2.6.7 ANOVA Multifactorial
El ANOVA multifactorial es una extensión del ANOVA unifactorial que permite analizar el efecto de dos o más factores independientes (o variables explicativas) sobre una variable dependiente. Mientras que el ANOVA unifactorial se centra en comparar las medias de un solo factor, el ANOVA multifactorial considera múltiples factores y sus posibles interacciones, lo que lo convierte en una herramienta más poderosa y flexible para el análisis de datos.
Este ANOVA extiende el ANOVA unifactorial:
Múltiples factores: En lugar de analizar un solo factor (por ejemplo, el efecto de un tipo de fertilizante en el crecimiento de las plantas), el ANOVA multifactorial permite estudiar varios factores simultáneamente (por ejemplo, el tipo de fertilizante y la cantidad de agua).
Interacciones entre factores: Una de las características más importantes del ANOVA multifactorial es su capacidad para evaluar si existe una interacción entre los factores. Esto significa que el efecto de un factor sobre la variable dependiente puede depender del nivel de otro factor. Por ejemplo, el efecto del fertilizante en el crecimiento de las plantas podría ser diferente dependiendo de la cantidad de agua aplicada.
Eficiencia en el diseño experimental: El ANOVA multifactorial permite estudiar múltiples factores en un solo experimento, lo que reduce el número de experimentos necesarios y aprovecha mejor los recursos.
Algunos retos del ANOVA multifactorial son:
Complejidad del diseño: A medida que se añaden más factores y niveles, el diseño experimental se vuelve más complejo y puede requerir un mayor número de observaciones.
Interpretación de interacciones: Las interacciones entre factores pueden ser difíciles de interpretar, especialmente cuando hay más de dos factores o cuando las interacciones son de orden superior (por ejemplo, interacciones de tres vías).
Supuestos más estrictos: Al igual que el ANOVA unifactorial, el ANOVA multifactorial requiere que se cumplan ciertos supuestos, como la normalidad, homogeneidad de varianzas e independencia de las observaciones. Sin embargo, en diseños multifactoriales, la violación de estos supuestos puede tener un impacto mayor en los resultados.
Algunas referencias bibliográficas para los interesados son
- Montgomery, D. C. (2017). Design and analysis of experiments. John wiley & sons.
- Kutner, M. H., Nachtsheim, C. J., Neter, J., & Li, W. (2005). Applied linear statistical models. McGraw-hill.
2.7 Intervalos y regiones de confianza
Además de los estimados puntuales de \(\boldsymbol{\beta}\) y \(\sigma^2\), también se pueden obtener estimados de intervalo de confianza para esos parámetros. El ancho de dichos intervalos es una medida de la calidad general del modelo lineal.
2.7.1 Regresion Lineal Simple
Intervalo de confianza para los parámetros
Si los errores se distribuyen en forma normal e independiente, entonces en el caso de la regresión lineal simple, tenemos las siguientes distribuciones de muestreo \[ \frac{\hat{\beta}_1-\beta_1}{\operatorname{se}\left(\hat{\beta}_1\right)} \sim t(n-2) \quad \text { y } \quad \frac{\hat{\beta}_0-\beta_0}{\operatorname{se}\left(\hat{\beta}_0\right)}\sim t(n-2). \] Así, un intervalo al \((1-\alpha)\times 100\%\) de confianza para la pendiente \(\beta_1\) es \[ \hat{\beta}_1-t (\alpha / 2 ; n-2) \operatorname{se}\left(\hat{\beta}_1\right)\ \leq \quad \beta_1 \quad \leq \ \hat{\beta}_1+t(a / 2; n-2) \operatorname{se}\left(\hat{\beta}_1\right), \]
y un intervalo al \((1-\alpha)\times 100\%\) de confianza para la ordenada al origen \(\beta_0\) es \[ \hat{\beta}_0-t(\alpha / 2; n-2) \operatorname{se}\left(\hat{\beta}_0\right)\ \leq \quad \beta_0 \quad \leq \ \hat{\beta}_0+t(\alpha / 2; n-2) \operatorname{se}\left(\hat{\beta}_0\right) \] donde, recordemos, \[ \operatorname{se}\left(\hat{\beta}_0\right)= \sqrt{s^2\left(\frac{1}{n}+\frac{\overline{\boldsymbol{x}}^2}{S_{xx}}\right)} \quad \text{ y }\quad \operatorname{se}\left(\hat{\beta}_1\right)= \sqrt{\frac{s^2}{S_{xx}}}. \]
Estos intervalos de confianza tienen la interpretación usual de frecuencia, por lo tanto, si hubiera que tomar muestras repetidas del mismo tamaño a los mismos valores de \(x\), y formar, por ejemplo, intervalos de confianza de \(95 \%\) de la pendiente para cada muestra, entonces el \(95 \%\) de esos intervalos contendrán el verdadero valor de \(\beta_1\).
En relación a \(\sigma^2\), tenemos que \[ (n-2) M S_{\mathrm{Res}} / \sigma^2 \sim \chi^2(n-2), \] así un intervalo al \((1-\alpha)\times 100\%\) de confianza para \(\sigma^2\) se puede obtener de \[ \mathbb{P}\left[\chi^2(1-\alpha / 2; n-2) \ \leq\quad \frac{(n-2) M S_{\text {Res }}}{\sigma^2} \quad \leq \ \chi^2(\alpha / 2; n-2)\,\right]=1-\alpha. \] El intervalo resultante para \(\sigma^2\) es \[ \frac{(n-2) M S_{\mathrm{Res}}}{\chi^2(\alpha / 2; n-2)}\ \leq \quad \sigma^2 \quad \leq \ \frac{(n-2) M S_{\mathrm{Res}}}{\chi^2(1-\alpha / 2; n-2)}. \]
Ejemplo: Intervalos de confianza para Regresión Lineal Simple
Código
# Parámetros del modelo
beta0 <- 2
beta1 <- 3
sigma2 <- 4
# Función para simular datos
simular_datos <- function(n) {
x <- rnorm(n, mean = 5, sd = 2) # Predictor x
epsilon <- rnorm(n, mean = 0, sd = sqrt(sigma2)) # Error
y <- beta0 + beta1 * x + epsilon # Variable respuesta
data.frame(x = x, y = y)
}
# Función para calcular intervalos de confianza
calcular_intervalos <- function(datos) {
# Ajustar el modelo
modelo <- lm(y ~ x, data = datos)
# Intervalos de confianza para beta0 y beta1
conf_int <- confint(modelo)
# Estimación de sigma^2
n <- nrow(datos)
sigma2_est <- sum(residuals(modelo)^2) / (n - 2)
# Intervalo de confianza para sigma^2 (usando distribución chi-cuadrado)
alpha <- 0.05 # Nivel de significancia del 95%
lower_sigma2 <- (n - 2) * sigma2_est / qchisq(1 - alpha/2, df = n - 2)
upper_sigma2 <- (n - 2) * sigma2_est / qchisq(alpha/2, df = n - 2)
# Resultados
list(
conf_int = conf_int, # Intervalos para beta0 y beta1
sigma2_est = sigma2_est, # Estimación de sigma^2
conf_int_sigma2 = c(lower_sigma2, upper_sigma2) # Intervalo para sigma^2
)
}
set.seed(121) # Para reproducibilidad
# Simular datos y calcular intervalos para diferentes tamaños de muestra
tamanos_muestra <- c(10, 50, 100)
resultados <- lapply(tamanos_muestra, function(n){
datos <- simular_datos(n)
intervalos <- calcular_intervalos(datos)
data.frame(
n = n,
parametro = c("beta0", "beta1", "sigma2"),
estimacion = c(coef(lm(y ~ x, data = datos)), intervalos$sigma2_est),
lower = c(intervalos$conf_int[1, 1], intervalos$conf_int[2, 1], intervalos$conf_int_sigma2[1]),
upper = c(intervalos$conf_int[1, 2], intervalos$conf_int[2, 2], intervalos$conf_int_sigma2[2])
)})
resultados <- do.call(rbind, resultados)
# Mostrar resultados
print(resultados)#> n parametro estimacion lower upper
#> (Intercept) 10 beta0 0.1040507 -5.6046846 5.812786
#> x 10 beta1 3.3747796 2.3119677 4.437591
#> 10 sigma2 4.4869692 2.0471447 16.467976
#> (Intercept)1 50 beta0 2.4852792 1.2219688 3.748590
#> x1 50 beta1 2.8714826 2.6237444 3.119221
#> 1 50 sigma2 2.8331797 1.9702627 4.421877
#> (Intercept)2 100 beta0 1.6200947 0.5281204 2.712069
#> x2 100 beta1 3.0395652 2.8317973 3.247333
#> 2 100 sigma2 3.9280585 3.0243830 5.309583Código
library(ggplot2)
# Crear la figura con ggplot2
ggplot(resultados, aes(x = factor(n), y = estimacion, ymin = lower, ymax = upper)) +
geom_pointrange(size = 2, fatten = 1.5) + # Aumentar grosor de la línea y tamaño del punto
facet_wrap(~ parametro, scales = "free_y", nrow = 1) + # Tres gráficas en una fila
labs(
x = "Tamaño de la muestra (n)",
y = "Estimación e intervalo de confianza",
title = "Intervalos de confianza para beta0, beta1 y sigma2",
subtitle = "A medida que aumenta el tamaño de la muestra"
) +
theme(
strip.text = element_text(size = 12, face = "bold"), # Formato de los títulos de las facetas
axis.title = element_text(size = 12),
plot.title = element_text(size = 14, face = "bold"),
panel.spacing = unit(1.5, "lines") # Espacio entre las gráficas
)
Intervalo de la respuesta media
Una aplicación importante de un modelo de regresión es estimar la respuesta media, \(\mathbb{E}(y\mid x_0)\). Se supone que \(x_0\) es cualquier valor de la variable regresora dentro del intervalo de los datos originales de \(x\) que se usaron para ajustar el modelo. Un estimador insesgado de \(\mathbb{E}\left(y \mid x_0\right)\) se determina a partir del modelo ajustado, como: \[ \widehat{E\left(y \mid x_0\right)}=\widehat{\mu}_{y \mid x_{\mathrm{a}}}=\widehat{\beta}_0+\widehat{\beta}_1 x_0. \]
Para obtener un intervalo al \((1-\alpha)\times 100\%\) de confianza para \(\mathbb{E}\left(y \mid x_0\right)\), notamos primero que \(\widehat{\mu}_{y l x_0}\) es una variable aleatoria con distribución Normal, ya que es una combinación lineal de \(\widehat{\beta}_0\) y \(\widehat{\beta}_1\) Normales e independientes.
A partir de las varianzas de \(\widehat{\beta}_0\) y \(\widehat{\beta}_1\), tenemos que la varianza de \(\widehat{\mu}_{y \mid x_0}\) es
\[ \begin{aligned} \operatorname{Var}\left(\widehat{\mu}_{y \mid x_0}\right) & =\operatorname{Var}\left(\widehat{\beta}_0+\widehat{\beta}_1 x_0\right)=\operatorname{Var}\left[\overline{y}+\widehat{\beta}_1\left(x_0-\overline{x}\right)\right] \\ & =\frac{\sigma^2}{n}+\frac{\sigma^2\left(x_0-\overline{x}\right)^2}{S_{x x}}=\sigma^2\left[\frac{1}{n}+\frac{\left(x_0-\overline{x}\right)^2}{S_{x x}}\right] \end{aligned} \] Así, la distribución de muestreo de \[ \frac{\widehat{\mu}_{y \mid x_0}-E\left(y \mid x_0\right)}{\sqrt{M S_{\operatorname{Res}}\left(1 / n+\left(x_0-\overline{x}\right)^2 / S_{x x}\right)}}= \frac{\frac{\widehat{\mu}_{y \mid x_0}-E\left(y \mid x_0\right)}{\sqrt{\sigma^2\left[\frac{1}{n}+\frac{\left(x_0-\overline{x}\right)^2}{S_{x x}}\right]}}}{\sqrt{\frac{(n-2)s^2/\sigma^2}{n-2}}}\sim t\,(n-2). \]
Entonces un intervalo al \((1-\alpha)\times 100\%\) de confianza para la respuesta media en el punto \(x=x_0\) es \[ \hat{\mu}_{y \mid x_0} \pm t\,(\alpha/2; n-2)\sqrt{M S_{\operatorname{Res}}\left(\frac{1}{n}+\frac{\left(x_0-\bar{x}\right)^2}{S_{x x}}\right)}. \] De esta expresión podemos ver que el ancho del intervalo alcanza un mínimo para \(x_0=\bar{x}\), y crece a medida que aumenta \(\left|x_0-\bar{x}\right|\). En forma intuitiva eso es razonable, porque cabría esperar que las mejores estimaciones de \(y\) se hacen con valores de \(x\) cerca del ceniro de los datos, y que la precisión de la estimación se redujera al moverse hacia la frontera del espacio de \(x\).
Ejemplo: Intervalos de confianza para Regresión Lineal Simple
Código
library(ggplot2)
# Simular datos
set.seed(123)
n <- 50
x <- runif(n, 0, 10)
epsilon <- rnorm(n, mean = 0, sd = 4)
y <- 2 + 3 * x + epsilon
datos <- data.frame(x = x, y = y)
# Ajustar el modelo lineal
modelo <- lm(y ~ x, data = datos)
# Crear un data.frame con valores de x para predecir
nuevos_x <- seq(min(x), max(x), length.out = 100)
predicciones <- predict(modelo, newdata = data.frame(x = nuevos_x), interval = "confidence", level=0.95)
# Combinar las predicciones con los valores de x
resultados <- data.frame(x = nuevos_x, fit = predicciones[, "fit"],
lwr = predicciones[, "lwr"], upr = predicciones[, "upr"])
# Graficar
ggplot(datos, aes(x = x, y = y)) +
# Graficar los puntos de los datos simulados
geom_point(size = 2, color = "blue", alpha = 0.7) +
# Graficar la línea del modelo ajustado
geom_line(data = resultados, aes(x = x, y = fit), color = "red", size = 1.2) +
# Graficar los intervalos de confianza para la media de Y
geom_ribbon(data = resultados, inherit.aes = FALSE, aes(x = x, ymin = lwr, ymax = upr),
fill = "orange", alpha = 0.5) +
# Etiquetas y título
labs(
x = "Predictor (x)",
y = "Respuesta (y)",
title = "Modelo lineal ajustado con intervalos de confianza",
subtitle = "Intervalos de confianza para la media de Y"
) +
# Tema minimalista
theme(
plot.title = element_text(size = 14, face = "bold"),
axis.title = element_text(size = 12)
)
Intervalo de predicción
A partir de Ecuación 2.4 vemos que el intervalo de predicción tiene en cuenta dos fuentes de incertidumbre:
- La incertidumbre en la estimación de los parámetros del modelo ( \(\beta_0\) y \(\beta_1\) ).
- La variabilidad de los datos (el término de error \(\epsilon\) ).
El intervalo de predicción al \((1-\alpha)\times 100 \%\) de confianza para \(y_0\) se calcula como: \[ \widehat{y}_0 \pm t(\alpha / 2; n-2) \sqrt{\operatorname{Var}\left(\widehat{y}_0\right) + MS_{\operatorname{Res}}} \]
Donde:
- \(t(\alpha / 2; n-2)\) es el percentil de la distribución \(t\) de Student con \(n-2\) grados de libertad (para un nivel de confianza \(1-\alpha\) ).
- \(\operatorname{Var}\left(\hat{y}_0\right)\) es la varianza de la predicción puntual.
- MS_{} es el error cuadrático medio (Mean Squared Error), que estima la varianza del término de error \(\sigma^2\).
La varianza de la predicción puntual \(\operatorname{Var}\left(\hat{y}_0\right)\) se calcula como: \[ \operatorname{Var}\left(\widehat{y}_0\right)=M S_{\operatorname{Res}}\left(1+\frac{1}{n}+\frac{\left(x_0-\overline{x}\right)^2}{\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}\right) \]
El intervalo de predicción al \((1-\alpha)\times 100 \%\) de confianza significa que, si repitiéramos el experimento muchas veces, el \(95\%\) de los intervalos calculados contendrían el valor real de \(y\) para \(x=x_0\). Es importante notar que este intervalo es más amplio que el intervalo de confianza para la media condicional, ya que incluye la incertidumbre adicional de la variabilidad de los datos.
Ejemplo: Intervalos de predicción
Consideramos los datos generaldos del ejemplo anterior.
Código
# Ajustar el modelo
modelo <- lm(y ~ x, data = datos)
# Definir el valor de x0 para el cual quieres predecir y
x0 <- data.frame(x = 5) # Consideramos x_0 = 5
# Calcular el intervalo de predicción al 95% de confianza
intervalo_prediccion <- predict(modelo, newdata = x0, interval = "prediction", level = 0.95)
# Mostrar el resultado
print(intervalo_prediccion)#> fit lwr upr
#> 1 17.19408 9.555568 24.83259Código
#
# Crear un data.frame con valores de x para predecir
nuevos_x <- seq(0, 15, length.out = 100)
predicciones <- predict(modelo, newdata = data.frame(x = nuevos_x), interval = "prediction", level=0.95)
# Combinar las predicciones con los valores de x
resultados <- data.frame(x = nuevos_x, fit = predicciones[, "fit"],
lwr = predicciones[, "lwr"], upr = predicciones[, "upr"])
# Graficar
ggplot(datos, aes(x = x, y = y)) +
# Graficar los puntos de los datos simulados
geom_point(size = 2, color = "blue", alpha = 0.7) +
# Graficar la línea del modelo ajustado
geom_line(data = resultados, aes(x = x, y = fit), color = "red", size = 1.2) +
# Graficar los intervalos de confianza para la media de Y
geom_ribbon(data = resultados, inherit.aes = FALSE,aes(x = x, ymin = lwr, ymax = upr),
fill = "orange", alpha = 0.5) +
# Etiquetas y título
labs(
x = "Predictor (x)",
y = "Respuesta (y)",
title = "Modelo lineal ajustado con intervalos de confianza",
subtitle = "Intervalos de confianza para la media de Y"
) +
# Tema minimalista
theme(
plot.title = element_text(size = 14, face = "bold"),
axis.title = element_text(size = 12)
)
2.7.2 Regresion Lineal (Múltiple)
Intervalo de confianza para los parámetros
Para construir estimados de intervalo de confianza de los coeficientes de regresión \(\beta_j\), usamos el hecho de que el estimador \(\widehat{\beta}\) es una combinación lineal de las observaciones y entonces tiene también distribución normal con vector medio \(\beta\) y matriz de covarianza \(\sigma^2\left(\mathbf{X}^{\top} \mathbf{X}\right)^{-1}\). Esto implica que la distribución marginal de cualquier coeficiente de regresión \(\widehat{\beta}_j\) es normal, con media \(\beta_j\) y varianza \(\sigma^2 C_{j j}\), donde \(C_{j j}\) es el \(j\)-ésimo elemento diagonal de la matriz \(\left(\mathbf{X}^{\top} \mathbf{X}\right)^{-1}\). En consecuencia, cada una de los estadísticos \[ \frac{\widehat{\beta}_j-{\beta}_j}{\sqrt{ MS_{\operatorname{Res}} C_{j j}}},\sim t\,(n-p) \quad j=0,1, \ldots, k. \] A partir de estos resultados podemos definir un intervalo de confianza de \((1-\alpha)\times 100%\) por ciento para el coeficiente de regresión \(\beta_j, j=0,1, \ldots, k\), como:
\[ \widehat{\beta}_j \pm t(\alpha / 2; n-p) \sqrt{ MS_{\operatorname{Res}} C_{j j}}. \]
Region de confianza para los parámetros
Ahora consideremos el problema de encontrar una región de confianza para el vector \(A^{\top}\boldsymbol{\beta}\). una región del \((1-\alpha)\times 100 \%\) de confianza para \(A^{\top}\boldsymbol{\beta}\) consiste en todos los vectores \(\boldsymbol{d}\) que no se rechazarian por una prueba estadística con nivel de \(\alpha\) para probar \(A^{\top} \boldsymbol{\beta}=\boldsymbol{d}\). Basados en los resultados que hasta ahora hemos obtenido, la región del \((1-\alpha) \times 100 \%\) de confianza consiste en todos los vectores \(\boldsymbol{d}\) que satisface la desigualdad \[ \begin{align} \frac{\left[A^{\top} \widehat{\boldsymbol{\beta}}-\boldsymbol{d}\right]^{\top}\left[A^{\top}\left(X^{\top} X\right)^{-1} A\right]^{-1}\left[A^{\top} \widehat{\boldsymbol{\beta}}-\boldsymbol{d}\right] / \operatorname{ran}(A)}{MS_{\operatorname{Res}}}\\[5pt] \leq F\,(1-\alpha;\ \operatorname{ran}(A),&\ \operatorname{ran}(I_n-P)) \end{align} \]
Estos vectores forman un elipsoide en \(\mathbb{R}^{\operatorname{ran}(A)}\).
Formas alternativas de esta región de confianza son \[ \begin{align} \left[A^{\top} \widehat{\boldsymbol{\beta}}-\boldsymbol{d}\right]^{\top}\left[A^{\top}\left(X^{\top} X\right)^{-1} A\right]^{-1}\left[A^{\top} \widehat{\boldsymbol{\beta}}-\boldsymbol{d}\right]\\[10pt] \leq \operatorname{ran}(A) \ MS_{\operatorname{Res}} F\,(1-\alpha;\ \operatorname{ran}(A),&\ \operatorname{ran}(I_n-P)). \end{align} \tag{2.19}\] Si tomamos \(M^{\top}=\left(X^{\top} X\right)^{-1} X^{\top}\), entonces \(A^{\top}=M^{\top} X = I_p\) y \(A^{\top}\boldsymbol{\beta}=\boldsymbol{\beta}=\boldsymbol{d}\). Así el término cuadrático de Ecuación 2.19 es \[ \begin{aligned} \left[A^{\top} \widehat{\boldsymbol{\beta}}-\boldsymbol{d}\right]^{\top}\left[A^{\top}\left(X^{\top} X\right)^{-1} A\right]^{-1}\left[A^{\top} \widehat{\boldsymbol{\beta}}-\boldsymbol{d}\right] & =(\widehat{\boldsymbol{\beta}}-\boldsymbol{\beta})^{\top}\left[\left(X^{\top} X\right)^{-1}\right]^{-1}(\widehat{\boldsymbol{\beta}}-\boldsymbol{\beta}) \\ & =(\hat{\boldsymbol{\beta}}-\boldsymbol{\beta})^{\top}\left(X^{\top} X\right)(\widehat{\boldsymbol{\beta}}-\boldsymbol{\beta}) \end{aligned} \]
con \(\operatorname{ran}(A)=\operatorname{ran}\left(I_p\right)=\operatorname{ran}(X)=p\). Entonces la región de confianza es el conjunto de \(\boldsymbol{\beta}\)’s tal que \[ (\widehat{\boldsymbol{\beta}}-\boldsymbol{\beta})^{\top}\left(X^{\top} X\right)(\widehat{\boldsymbol{\beta}}-\boldsymbol{\beta}) \leq p \ MS_{\operatorname{Res}}\ F\,(1-\alpha; \ p, \ n-p) \]
Ejemplo: Región 95% de confianza
Código
autompg <- read.table(
"http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data", quote = "\"", comment.char = "", stringsAsFactors = FALSE)
colnames(autompg) <- c("mpg", "cyl", "disp", "hp", "wt", "acc", "year",
"origin", "name")
autompg <- subset(autompg, autompg$hp != "?")
autompg <- subset(autompg, autompg$name != "plymouth reliant")
rownames(autompg) <- paste(autompg$cyl, "cylinder", autompg$year, autompg$name)
autompg <- subset(autompg, select = c("mpg", "cyl", "disp", "hp", "wt", "acc", "year"))
autompg$hp <- as.numeric(autompg$hp)
str(autompg)#> 'data.frame': 390 obs. of 7 variables:
#> $ mpg : num 18 15 18 16 17 15 14 14 14 15 ...
#> $ cyl : int 8 8 8 8 8 8 8 8 8 8 ...
#> $ disp: num 307 350 318 304 302 429 454 440 455 390 ...
#> $ hp : num 130 165 150 150 140 198 220 215 225 190 ...
#> $ wt : num 3504 3693 3436 3433 3449 ...
#> $ acc : num 12 11.5 11 12 10.5 10 9 8.5 10 8.5 ...
#> $ year: int 70 70 70 70 70 70 70 70 70 70 ...Código
modelo <- lm(mpg ~ wt + hp,data = autompg)
beta_g<-as.vector(modelo$coefficients)
x<-cbind(autompg$wt,autompg$hp,autompg$cyl)
A<-matrix(c(0,1,0,0,0,1),3,2)
x0<-c(0,0)
MS_Res <- sum(modelo$residuals^2)/modelo$df.residual
lev<-function(x0){
t(t(A)%*%beta_g-x0)%*%solve(t(A)%*%solve(t(x)%*%x)%*%A)%*%(t(A)%*%beta_g-x0)/(2*MS_Res)
}
xgrid <- seq(-0.04, 0.03, length.out = 100)
ygrid <- seq(-0.8, 0.7, length.out = 100)
grid <- expand.grid(x = xgrid, y = ygrid)
grid$z <- apply(grid, 1, lev)
library(ggplot2)
heatmap_plot <- ggplot(grid, aes(x = x, y = y, fill = z)) +
geom_tile() +
scale_fill_viridis_c() +
theme_minimal() #+
labs(
title = "",
x = expression(beta[1]), # Eje x: beta_1
y = expression(beta[2]), # Eje y: beta_2
)#> $x
#> expression(beta[1])
#>
#> $y
#> expression(beta[2])
#>
#> $title
#> [1] ""
#>
#> attr(,"class")
#> [1] "labels"Código
print(heatmap_plot)
2.8 Teorema de Gauss-Markov
El Teorema de Gauss-Márkov es un conjunto de supuestos que debe cumplir un estimador MCO (Mínimo Cuadrados Ordinarios) para que se considere como estimador lineal insesgado óptimo. El Teorema de Gauss-Márkov fue formulado por Carl Friederich Gauss y Andréi Márkov.
El teorema de Gauss-Markov establece que el estimador de mínimos cuadrados ordinarios (OLS, ordinary least-squares) de \(\beta\), que es \(\widehat{\boldsymbol{\beta}}=\left(X^{\top} X\right)^{-1} X^{\top} \boldsymbol{Y}\), es el mejor estimador lineal insesgado (BLUE, Best linear unbiased estimator). En este caso, mejor quiere decir que \(\widehat{\boldsymbol{\beta}}\) tiene la mínima varianza, en cierto sentido significativo, entre la clase de todos los estimadores insesgados que son combinaciones lineales de los datos.
Un problema es que \(\widehat{\boldsymbol{\beta}}\) es un vector, y en consecuencia, su varianza es en realidad una matriz. Por ello se tratará de demostrar que \(\widehat{\boldsymbol{\beta}}\) minimiza la varianza para cualquier combinación lineal de los coeficientes estimados, \(\boldsymbol{\ell}^{\top} \widehat{\boldsymbol{\beta}}\). Se observa que \[ \begin{aligned} \operatorname{Var}(\boldsymbol{\ell}^{\top} \widehat{\boldsymbol{\beta}}) & =\boldsymbol{\ell}^{\top} \operatorname{Var}(\widehat{\boldsymbol{\beta}}) \boldsymbol{\ell} \\ & =\boldsymbol{\ell}^{\top}\left[\sigma^2\left(X^{\top} X\right)^{-1}\right] \boldsymbol{\ell} \\ & =\sigma^2 \boldsymbol{\ell}^{\top}\left(X^{\top} X\right)^{-1} \boldsymbol{\ell} \end{aligned} \] es un escalar.
Entonce si consideramos otro estimador insesgado de \(\boldsymbol{\beta}\), \(\widetilde{\boldsymbol{\beta}}\), que es una combinación lineal de los datos. Lo que queremos es demostrar que
\[
\operatorname{Var}\left(\boldsymbol{\ell}^{\top} \widetilde{\boldsymbol{\beta}}\right) \geq \operatorname{Var}\left(\boldsymbol{\ell}^{\top} \widehat{\boldsymbol{\beta}}\right).
\]
Primero, observamos que podemos escribir cualquier otro estimador de \(\boldsymbol{\beta}\) que sea una combinación lineal de los datos en la forma \[ \widetilde{\boldsymbol{\beta}}=\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right] \boldsymbol{Y}+\boldsymbol{b}_0 \] donde \(B\) es una matriz de \(p \times n\), y \(\boldsymbol{b}_0\) es un vector, \(p \times 1\), de constantes, que ajusta en forma adecuada al estimador de mínimos cuadrados para formar el estimado alternativo. A continuación observamos que \[ \begin{aligned} \mathbb{E}(\widetilde{\boldsymbol{\beta}}) & =E\left(\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right] \boldsymbol{Y}+\boldsymbol{b}_0\right) \\ & =\left[\left(X^{\top} X^{-1} X^{\top}+B\right] \mathbb{E}(\boldsymbol{Y})+\boldsymbol{b}_0\right. \\ & =\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right] X \boldsymbol{\beta}+\boldsymbol{b}_0 \\ & =\left(X^{\top} X\right)^{-1} X^{\top} X \boldsymbol{\beta}+B X \boldsymbol{\beta}+\boldsymbol{b}_0 \\ & =\boldsymbol{\beta}+B X \boldsymbol{\beta}+\boldsymbol{b}_0. \end{aligned}\\ \] Por consiguiente, \(\tilde{\boldsymbol{\beta}}\) es insesgado si, y sólo si \(\boldsymbol{b}_0=\boldsymbol{0}\) y \(BX=0\). Por otro lado, la varianza de \(\tilde{\boldsymbol{\beta}}\) es \[ \begin{aligned} \operatorname{Var}(\widetilde{\boldsymbol{\beta}}) & =\operatorname{Var}\left(\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right] \boldsymbol{Y}\right) \\ & =\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right] \operatorname{Var}(\boldsymbol{Y})\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right]^{\top} \\ & =\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right] \sigma^2 I_n\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right]^{\top} \\ & =\sigma^2\left[\left(X^{\top} X\right)^{-1} X^{\top}+B\right]\left[X\left(X^{\top} X\right)^{-1}+B^{\top}\right] \\ & =\sigma^2\left[\left(X^{\top} X\right)^{-1}+B B^{\top}\right]. \end{aligned} \] Los terminos cruzados se anularon porque \(B X=0\) (así también \(B X^{\top}=X^{\top}B^{\top}=0\)).
Entonces, \[ \begin{aligned} \operatorname{Var}\left(\boldsymbol{\ell}^{\top} \widetilde{\boldsymbol{\beta}}\right) & =\boldsymbol{\ell}^{\top} \operatorname{Var}(\widetilde{\boldsymbol{\beta}}) \boldsymbol{\ell} \\ & =\boldsymbol{\ell}^{\top}\left(\sigma^2\left[\left(X^{\top} X\right)^{-1}+B B^{\top}\right]\right) \boldsymbol{\ell} \\ & =\sigma^2 \boldsymbol{\ell}^{\top}\left(X^{\top} X\right)^{-1} \boldsymbol{\ell}+\sigma^2 \boldsymbol{\ell}^{\top} B B^{\top} \boldsymbol{\ell} \\ & =\operatorname{Var}\left(\boldsymbol{\ell}^{\top} \widetilde{\boldsymbol{\beta}}\right)+\sigma^2 \boldsymbol{\ell}^{\top} BB^{\top} \boldsymbol{\ell}. \end{aligned} \] Primero se observa que \(B B^{\top}\) es una matriz positiva semidefinida, y por consiguiente \(\sigma^2 \boldsymbol{\ell}^{\top} B B^{\top} \boldsymbol{\ell} \geq 0\). A continuación, se ve que se puede definir a \(\boldsymbol{\ell}^*=B^{\top} \boldsymbol{\ell}\). Por consiguiente, \[ \boldsymbol{\ell}^{\top} B B^{\top} \boldsymbol{\ell}=\boldsymbol{\ell}^{* \top} \boldsymbol{\ell}^*=\sum_{i=1}^p \ell_i^{* 2} \]
que debe ser estrictamente mayor que 0 para cierta \(\boldsymbol{\ell} \neq \boldsymbol{0}\), a menos que \(B=\mathbf{0}\). Por lo anterior, el estimado de mínimos cuadrados de \(\beta\) es el mejor estimador lineal insesgado.
Bibliografía:
- Christensen, R. (2011). Plane answers to complex questions: The Theory of Linear Models. 4th Ed. New York: Springer.
- Christensen, R. (1996). Analysis of variance, design, and regression: Applied statistical methods. CRC press.
- Montgomery, D. C., Peck, E. A., & Vining, G. G. (2021). Introduction to linear regression analysis. John Wiley & Sons.