Kepler orbits geometry

(Under construction. Last modified: .)

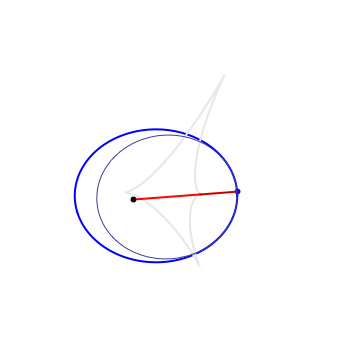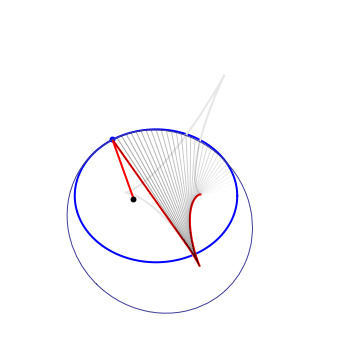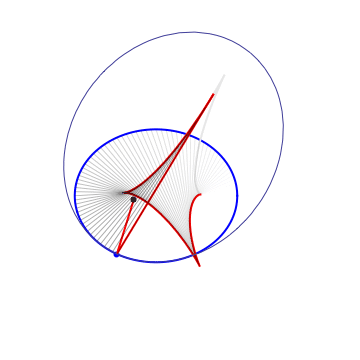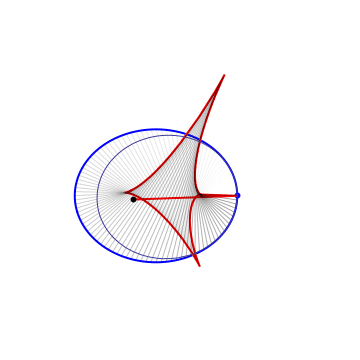
Definitions. A Kepler orbit is a conic (ellipse, parabola or hyperbola) with one focus at the origin. It is the orthogonal projection on the $xy$ plane of sections of $x^2+y^2=z^2$ by a 2-plane $ax+by+cz=1$, $c\neq 0$. The eccentricity is $e=\sqrt{a^2+b^2}/|c|$. In case of hyperbola ($e>1$) only the branch going around the origin is taken. Given a plane curve $\gamma$, strictly convex wrt 0, it can be aproximated at each pt to 2nd order by a unique Kepler conic, the osculating Kepler orbit. The pts of $\gamma$ where the osculating conic hyperosculates (3rd order tangency) are the (Kepler) vertices. For a closed simple curve there are at least 4 vertices (the 4v thm). Between vertices, the osculating conics are nested. The Kepler evolute of $\gamma$ is the curve $\Gamma$ traced by the 2nd focus of the osculating conic. The vertices of $\gamma$ correspond to the cusps of $\Gamma$. $\Gamma$ is also the envelope of the light rays emenating from the origin and reflected by $\gamma$ (the caustic). The Kepler involute of $\Gamma$ is obtained by a string construction, where one fixes a length of string and tie its end pts at a fixed pt of $\Gamma$ and the origin, then trace a curve while keeping the string tight.

Gallery

Conic sections

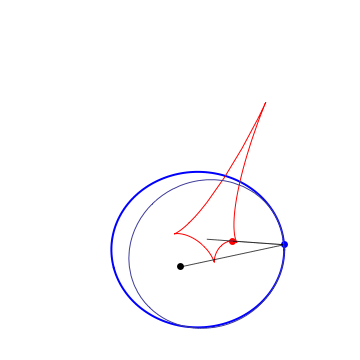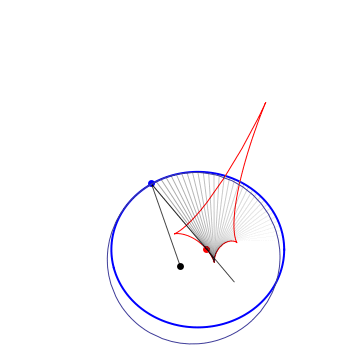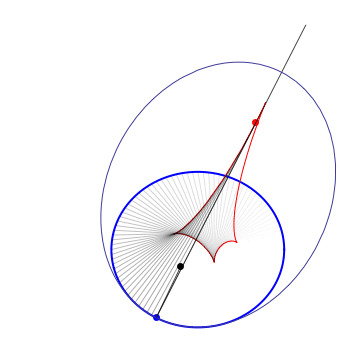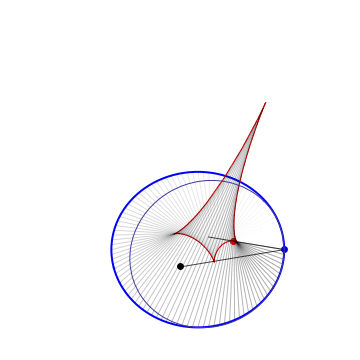
Osculating ellipses

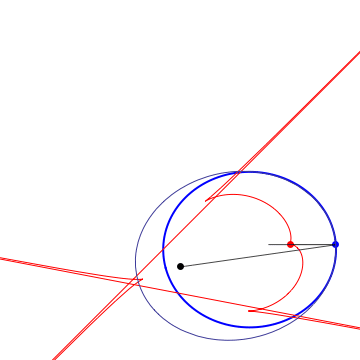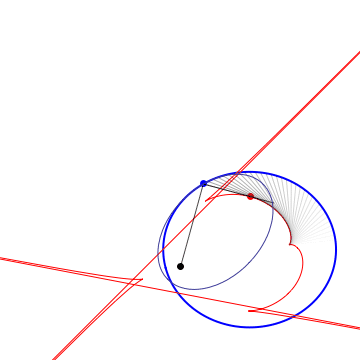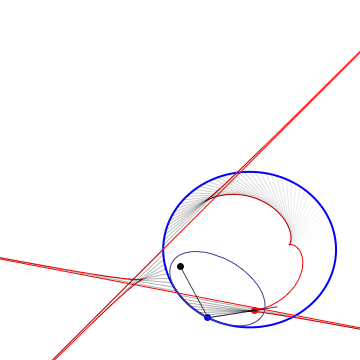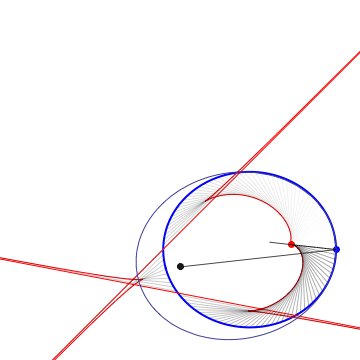
Osculating ellipses + hyperbolas

String contruction