Next: Conclusión Up: Indice Previous: Problema de bondad de ajuste

Pruebas de bondad de ajuste

La idea de una prueba de bondad de ajuste es comparar el histograma,,con la mejor densidad de Poisson que le queda a los datos. Si la discrepancia entre éstos es demasiado grande, entonces se habla de evidencia en contra del hecho de que f(x) sea Poisson (recuerda que por la Ley de los Grandes Números, siempre se parece a f(x), sin importar si ésta última es o no de Poisson).

Hay teoría matemática (llamada máxima verosimilitud) que dice que, en cierto sentido, la mejor densidad de Poisson que le queda a los datos es aquella que tiene parámetro dado por Es decir, el problema se reduce a comparar con

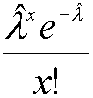
Cómo comparar entre sí las dos funciones y ? Esto es equivalente a comparar entre sí

y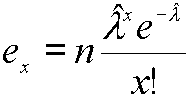

(la letra e es por frecuencia ``esperada'' bajo la densidad de Poisson).

Una forma de comparar las ox con las ex es calculando el valor de

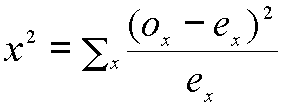
La cantidad se llama estadística de prueba para bondad de ajustegif. Para entenderla intuitivamente, debes notar que

La moraleja es que es una medida de discrepancia entre las ox y ex las que se esperarían bajo una densidad de Poisson.

Se dice que es demasiado grande si excede cierto valor C que depende de cuántas categorías de x hubo (los valores de C se encuentran calculados por teoría estadística y se anotan en tablas).

Un resultado matemático establece lo siguiente:

Si la densidad f(x) es Poisson, entonces la probabilidad de que exceda C es solo del 5%.

Esto quiere decir que si se obtiene una muestra de X, y se calcula un valor de que resulta demasiado grande, entonces hay dos posibles explicaciones para ello:

A f(x) es Poisson y tuve buenísima suerte, pues me ocurrió algo que tenía sólo probabilidad 5% de ocurrir
B f(x) no es Poisson, y por eso me salió un valor de demasiado grande

Asumir la explicación A es creer que sólo la suerte explica las cosas y que la naturaleza nos juega bromas con cosas poco probables. La explicación B es mucho más razonable. La explicación A es posible, pero poco probable.

De hecho, se trata exactamente del razonamiento que usamos en las siguientes dos situaciones:

Situación análoga #1: Suponer que el director de la Lotería Nacional se ganó dos veces seguidas el Premio Mayor. Hay dos posibles explicaciones para ello:

A
El Director de la LN tuvo una suerte tremenda, pues le ocurrió algo que tenía sólo probabilidad .0000000004 de ocurrir
B
La urna de la LN estuvo intervenida, y por eso ocurrió que el Director de la LN ganó dos veces seguidas

Estarán de acuerdo que B es la explicación natural que elegimos.

Situación análoga #2: El mago me adivinó la carta que secretamente elegí. Hay dos explicaciones para ello:

A
El mago tuvo mucha suerte, pues en realidad me la adivinó al azar, lo cual tiene sólo probabilidad 1/52=.019 de ocurrir
B
El mago tiene poderes mágicos legítimos, y por eso me la pudo adivinar

La explicación B es la que siempre preferimos; por eso nos maravillamos ante el truco del mago.

Conclusión: si , se interpreta como evidencia en contra de la suposición de que f(x) sea Poisson, y si entonces se concluye que no hay razón para sospechar que f(x) no sea de Poisson. La posibilidad de que yo concluya erróneamente que f(x) no es de Poisson cuando realmente sí lo sea, es sólo del 5%.