Up: Indice Previous: Conclusión
Ejercicios
1. Piensa en ejemplos específicos en algunas ciencias experimentales,
que den lugar a:
(a)Variables aleatorias que sí sean de conteo
(b)Variables aleatorias que no sean de conteo
- El que un fenómeno sea aleatorio o no, no sólo depende
del fenómeno en sí mismo sino de quién lo esté
observando. Por ejemplo, los astrónomos de hoy saben perfectamente
bien cuándo será el próximo eclipse solar y estrictamente
hablando se trata de un fenómeno determinístico. Sin embargo,
para un observador de la prehistoria, los eclipses eran fenómenos
aleatorios en el sentido de que no era posible predecirlos por no haberse
desarrollado aún el conocimiento en mecánica celeste. Piensa
en un ejemplo más de un fenómeno que para un observador puede
ser aleatorio y para otro, determinístico.
- Calcula y grafica la densidad de Poisson para distintos valores de
su parámetro (o puedes basarte en la Figura
 ).
Observarás que la densidad tiende a acumularse alrededor de un valor
central, el cual en teoría de probabilidad se llama el valor
esperado de la densidad, o esperanza de la densidad. Examina
las gráficas anteriores para descubrir la respuesta a la siguiente
pregunta: Cuál es el valor del valor esperado de una densidad de
Poisson, como función de ?
).
Observarás que la densidad tiende a acumularse alrededor de un valor
central, el cual en teoría de probabilidad se llama el valor
esperado de la densidad, o esperanza de la densidad. Examina
las gráficas anteriores para descubrir la respuesta a la siguiente
pregunta: Cuál es el valor del valor esperado de una densidad de
Poisson, como función de ?
- Obtén datos observando las siguientes situaciones, construye
histogramas, y ejecuta con ellos pruebas de bondad de ajuste a una densidad
de Poisson:
- Cuenta el número de automóviles que pasan por una avenida
en intervalos de 2 minutos.
- Elige personas al azar, y que te digan cuántos hijos tienen.
- Cuenta el número de errores tipográficos por renglón
en algún escrito mecanografiado por alguna persona.
- La binomial es otra densidad aplicable a variables aleatorias
de conteo, y está dada por
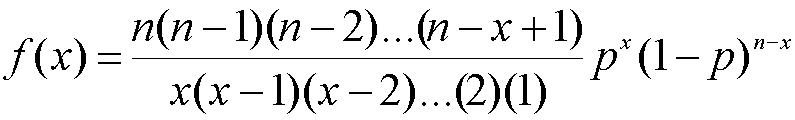
para Esta densidad tiene DOS parámetros: n que es un número
entero positivo, y p, que es un número entre cero y uno.
Una aplicación de esta densidad es la siguiente: Si lanzas una moneda
n veces, siendo que la probabilidad de un águila es 1/2,
y defines la variable aleatoria X como el número total de
águilas que obtienes en los n lanzamientos, entonces f(x)
(con p=1/2) te da la probabilidad de que X tome el valor
x. En la Figura  se grafica la densidad binomial para n=9 y p=.8.
se grafica la densidad binomial para n=9 y p=.8.
- En la densidad binomial ahora toma n=200 y p=.01. Calcula
la densidad binomial para los valores
- Compara con los valores calculados anteriormente de la densidad de
Poisson para y descubrirás algo asombroso. De hecho, fue de este
modo que S. D. Poisson descubrió la densidad que hoy lleva su nombre.
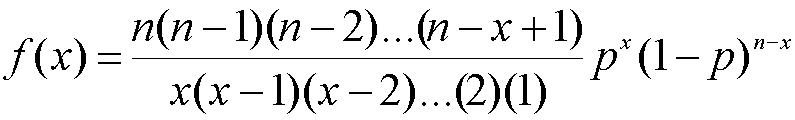
![]() se grafica la densidad binomial para n=9 y p=.8.
se grafica la densidad binomial para n=9 y p=.8.