LOGO Pensamiento matemático para amantes de las matemáticas, feb-jun 2009
Centro de Investigación en Matemáticas, Guanajuato
http://www.cimat.mx/ciencia_para_jovenes/pensamiento_matematico

Sexta sesión (3 abr 2009)

Las "Torres de Hanoi"
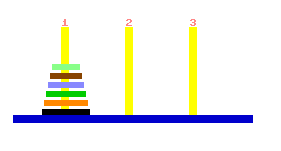
Tenemos tres varillas verticales y N discos de tamaños distintos, colocados de mayor a menor ascendentemente en la primera varilla. El reto consiste en transportar todos los discos a la tercera varilla, colocados de mayor a menor ascendentemente. Esto se hace por una serie de pasos; un "paso" consiste en mover uno de los discos que se encuentra en una de las varillas (el mas alto en esta varilla) a otra varilla, pero siempre poniendo un disco menor sobre un disco mayor.

La pregunta es si es posible lograr el objetivo del juego y en caso que si, cual es el mínimo numero de pasos necesarios para lograr el objetivo.

Solucion: para pasar el disco mas grande a la tercera varilla, tenemos que transportar primero los primeros N-1 discos de la primera varilla a la segunda varilla en el mínimo numero de pasos, luego mover el disco mas grande a la tercera varilla, luego transportar los N-1 discos de la segunda varilla a la tercera en el menor numero de pasos. Para transportar los primeros N-1 discos de la primera columna a la segunda, aplicamos el mismo razonamiento, solamento intercambiando los papeles de la segunda y tercera varilla, y con N-1 discos en lugar de N discos, y asi sucecivamente...

Asi que:
Para N=1 se resuelve el problema en 1 paso;
Para N=2 se resuelve el problema en 1+1+1=3 pasos;
Para N=3 se resuelve el problema en 3+1+3=7 pasos;
Para N=4 se resuelve el problema en 7+1+7=15 pasos;
.
.
.
Para N discos se resuelve el problema en 2N-1 pasos.

Reto: Si tenemos 4 varillas y 5 discos, ¿cuál es el mínimo número de movimientos necesarios para transportar todos los discos de la varilla uno a la cuatro? ¿Y si hubieran 4 varillas y 10 discos?

Acertijo Matemático

A una aldeas llegan unos magos poderosos y colocan a todos los humanos en fila india, desde el mas bajo hasta el mas alto (el ultimo en la fila), de modo que cada persona en la fila ve a todos las personas en frente de el en la fila. Luego los magos van poniendo un sombrero, blanco o negro aleatoriamente, a cada persona en la fila. Luego empiezan a preguntar, empezando con el ultimo en la fila (el mas alto), de que color es tu sombrero? Si acierta - vive, y si falla - muere.

La pregunta es: ¿Que estrategia se te ocurre para salvar la mayor cantidad de vidas posible?

NOTA: las personas en la fila no pueden hablar entre ellos, ni hacer gestos, ni moverse; la única acción que pueden hacer los humanos es decir BLANCO o NEGRO, y todos los demás aldeanos son capaces de oir la respuesta de los demás. Tampoco pueden saber si mueren o viven los aldeanos detras de cada uno.