 Pensamiento matemático para amantes de las matemáticas, feb-jun 2009
Pensamiento matemático para amantes de las matemáticas, feb-jun 2009
Centro de Investigación en Matemáticas, Guanajuato
http://www.cimat.mx/ciencia_para_jovenes/pensamiento_matematico
Onceava sesión (5 junio 2009)
Los 13 Monjes
Los 13 monjes de un monasterio son puestos a la prueba siguiente:
cada uno de los monjes se marca su frente con azul o rojo. Cada monje puede ver las marcas de los demas pero no la suya.
Cada día los monjes se reúnen para comer y si uno de ellos se da cuenta que tiene marca roja en su frente debe dejar el monasterio.
Los monjes saben que por lo menos uno de ellos tiene marca roja pero no saben cuantos monjes estan marcados con rojo. Los monjes no pueden comunicarse entre sí.
La prueba acaba cuando todos los monjes con marca roja dejaron el monasterio.
¿Cuántos días necesitarán para completar la prueba si hay 1 monje con marca roja? 2 monjes? 5 monjes?
El reto de los cuatro cuatros
Usando exactamente cuatro cuatros y todas las operaciones matemáticas que quieras, forma los números del 1 al 10.
Por ejemplo:
1=44/44,
2=4/4+4/4.
Casados y Viudos.
En una ciudad hay 100 hombres. 53 de
ellos están casados (por la primera o la segunda vez), 32 nunca
se casaron, 15 enviudaron y 5 se divorciaron de su primera mujer
y no volvieron a casarse. ¿Cuantos enviudaron y volvieron a casarse?
Simplificación con suerte
Considera la fracción 16/64. Si simplificamos tachando la cifra 6, presente en las unidades del numerador y en las decenas del denominador,
nos queda la fracción 1/4 que, inesperadamente, es equivalente a la anterior.
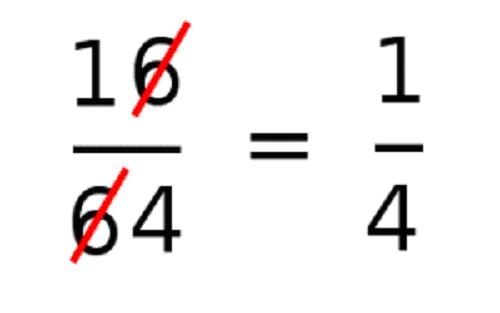
Es decir, el método es absolutamente incorrecto, pero el resultado es cierto.
¿Puedes encontrar todas las fracciones, cuyos numerador y denominador tengan también dos cifras, que cumplan esta curiosa propiedad?
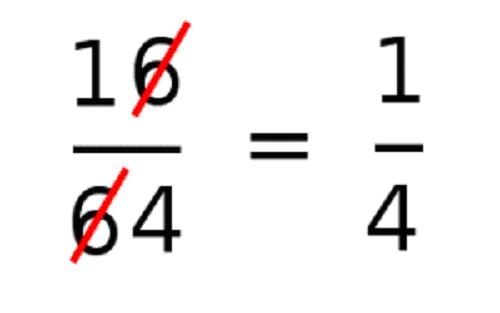
 Pensamiento matemático para amantes de las matemáticas, feb-jun 2009
Pensamiento matemático para amantes de las matemáticas, feb-jun 2009