Fracciones continuas, números de Fibonacci y la razón áurea: Considera las siguientes fracciones:
1, 1+ 1/1, 1+1/(1+1), 1+1/(1+1/(1+1)), 1+1/(1+1/(1+1)), 1+1/(1+1/(1+1+1/(1+1))), ...
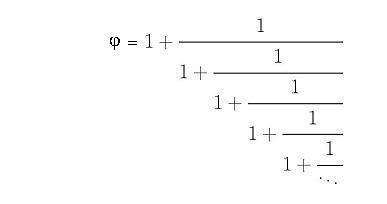
Estas fracciones, al simplificarlas, son de la forma Fn+1/Fn, y tienden a la razón áurea. Asi obtenemos una expresión para la razón áurea como "fracción contínua":
La paradoja de Curry
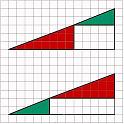
| Considera un triángulo rectángulo (rojo) de catetos de longitudes 8 y 3,
y otro triángulo rectángulo (verde) de catetos de longitudes 5 y 2. Estos dos triángulos podemos acomodar en un triángulo rectángulo de
catetos de longitudes 13 y 5. Hay dos acomodos, en uno el triángulo verde queda más arriba del rojo y en el
otro arreglo queda más abajo. En un acomodo sobra un area de 15 y en el otro 16. ¿Cómo es posible?
|
 |
Esto se puede hacer con cualquer 4 números de Fibonacci sucesivos,
Fn, Fn+1, Fn+2, Fn+3
(el ejemplo arriba corresponde a n=3). Mientras más grande la n más dificil es notar "la trampa". La propiedad de los números de Fibonacci en la que está basado el efecto es FnFn+3- Fn+1Fn+2= ±1 .
Triángulo de Pascal y los números de Fibonacci
| Coloca el número "1" en un papel. Abajo, en segundo renglón, coloca dos "1". A partir de allí, cada renglón comienza y termina con un "1", y abajo del punto medio de cada par de números consecutivos del renglón
anterior se coloca su suma. El triángulo (infinito) de números obtenido de este modo se conoce como
el "triángulo de Pascal".
|

|
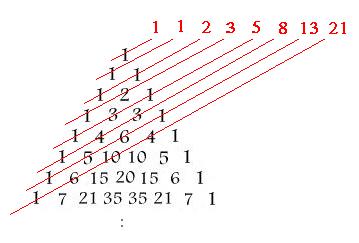
| Diagonales: Las sumas de los números sobre los "diagonales" en el dibujo son los números de Fibonacci.
|
|
| 
 Otra cara de las matemáticas, CIMAT, mar-jun 2010.
Otra cara de las matemáticas, CIMAT, mar-jun 2010.



