Otra cara de las matemáticas

Otra cara de las matemáticas, CIMAT, mar-jun 2010.
http://www.cimat.mx/ciencia_para_jovenes/otra_cara

Segunda sesión (11 mar 2010)

Invariantes que ayudan ganar juegos

10 (ver notas de la sesion pasada): se empieza con un monton de 10 piedras (digamos). Cada jugador en su turno quita 1 o 2 piedras del monton. Gana quien quita la última piedra.
El invariante: el resíduo al dividir el número de piedras en el monton entre 3. El valor de este puede ser 0, 1 ó 2. Si dejas el resíduo 0, tu compañero lo tiene que cambiar a 1 o 2, y luego lo puedes regresar a 0.
10,11: empezamos con dos montones de piedra, con 10 y 11 piedras. Cada jugador en su turno puede quitar 1 o 2 piedras de uno de los montones, o una piedra de ambos (si ambos montones todavia les quedan piedras). Gana quien quita la última piedra.
El invariante: el resíduo al dividir la suma de los números de las piedras en los dos montones entre 3. El valor de este puede ser 0, 1 ó 2. Si dejas el resíduo 0, tu compañero lo tiene que cambiar a 1 o 2 y luego lo puedes regresar a 0.

Invariantes para demostrar la imposibilidad de unos retos

Diferencias: En el pizarrón escribes los números 1, 2, 3,...,10. En cada turno puedes borrar dos números del pizarrón y escribir al final su dferencia. Continua hasta que quede solo un número en el pizarrón. ¿Puede ese número ser 2?
El invariante: la paridad de la suma de los números en el pisaron (Otro modo: el resíduo al dividir la suma entre 2). Esta no cambia al sustituir un par de los números por su diferencia.

Velas: Tu padre cumple 60 años. Su pastel se corta en 6 rebanadas triángulares y luego se le colocan las 60 velas.

Al principio colocas un par de velas, en dos rebanadas distintas, separadas por una rebanada.

Pero luego, tu padre te pide, que el resto de las velas las coloques de par en par, tal que cada par de velas se ubiquen en 2 rebandas adyacentes (justo lo que no hiciste con el primer par de velas...). Además, quiere que al terminar de poner las velas, cada rebanada tenga la misma cantidad de velas (10 velas en cada rebanada). ¿Podrás satisfacer a tu padre?

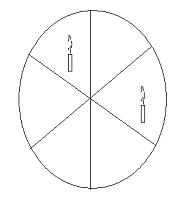
Mapas: puedes dibujar (en el plano) un mapa que tenga 4 países, 6 fronteras y 4 vértices (puntos en donde se unen 2 o más fronteras)?
El invariante: P-F+V (el invariante de Euler). En el plano, siempre es 1.
El reto del 15 : Un reto popular consiste en un cuadro de 4 x 4 en donde están ubicadas 15 fichas de 1 x 1 con los números del 1 al 15, dejando un cuadrito vacío. Cualquer ficha adyacente al cuadrito vacío la puedes mover al lugar vacío (dejando un lugar vacío donde estaba la ficha).
El objetivo del juego es lograr diversos patrones de las fichas. Un tal reto es, empezando con las fichas en cierto patron, lograr intercambiar la posición de dos de las fichas (digamos 14 y 15), sin afectar la posición de las demas fichas. ¿Es posible cumplir tal reto?
El invariante: se asocia con cada patron de las fichas una paridad ("par" o "impar"), que es la suma de dos paridades, A y B (ver más abajo la definción de "suma de paridades").
La paridad A: se marca todos los 16 lugares de la tabla con los números 1 hasta 16 (digamos de la manera "estandar"). De este modo, dado un patron de las fichas, cada ficha (incluyendo el cuadrado vacío, que marcamos como "ficha 16"), digamos x (un número entre 1 y 16), tiene su lugar x' (otro número entre 1 y 16). Para determinar A se checa para cada par de fichas marcadas con x,y, con x < y, si sus lugares, x',y', satisfacen x' < y' o no. Entonces A es la paridad del número de pares x,y tal que x'>y'.
La paridad B: es la paridad de 16' (la paridad del lugar de la ficha vacía).
Suma de paridades: par + par = par, par + impar = impar, impar + impar = impar.
Luego se observa que al mover una ficha al lugar vacío, ambas paridades A y B cambian, así que su suma no cambia. Al intercambiar dos fichas (de 1 a 15), cambia solo A, así que la suma sí cambia.