Fronts and caustics in billiard tables

(Under construction. Last modified: .)

Definitions. Pick an initial point inside a convex smooth curve and shine light from it (or shoot billiard balls) in all directions. When a light ray reaches the boundary it is reflected as usual. The envelope of the beam after $n$-reflections is the $n$-th caustic wrt the initial point. Theorem: for a generic initial point each caustic has $\geq 4$ cusps. Conjecture: for an ellipse there are exactly 4 cusps. The wave front at time $t$ is the locus of pts reached by all light rays after $t$ time units.

Gallery

Evolving wave fronts inside an ellipse
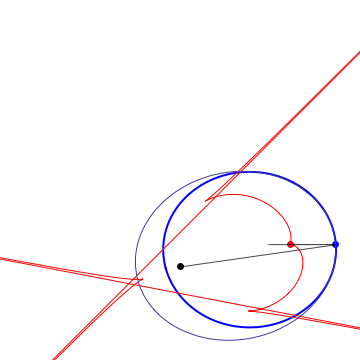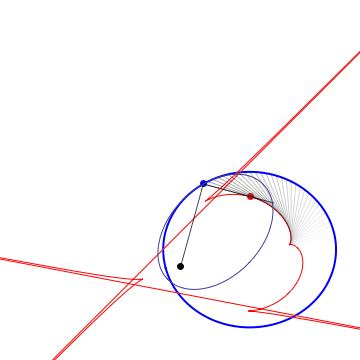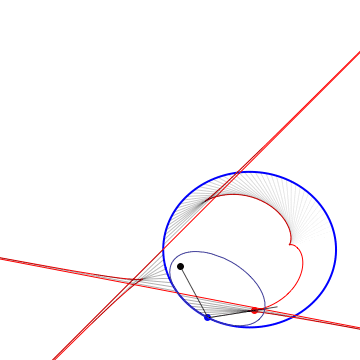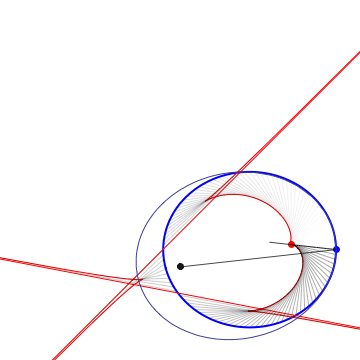
The 1st Caustic	The 1st Caustic, different initial point
The 2nd Caustic	The 3rd Caustic
The 1st Caustic (red) with a smooth involute (green)	Same, different initial point
An involute (green) of the 1st caustic (red)	Same for the 2nd caustic
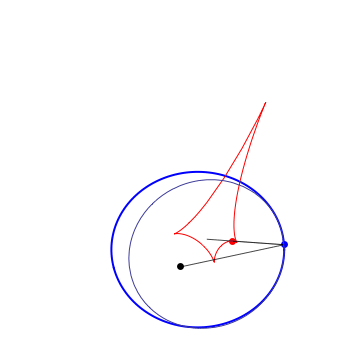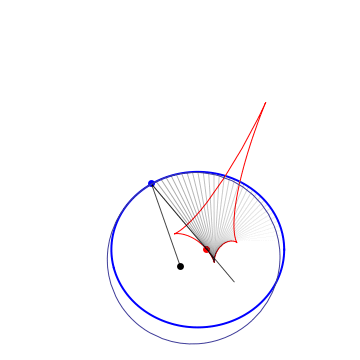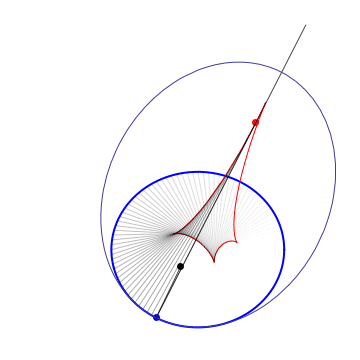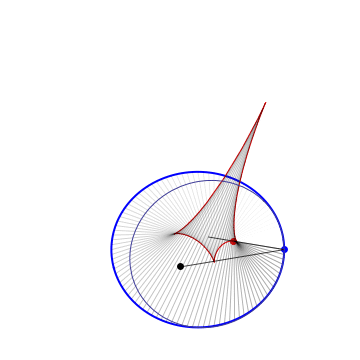
The 1st caustic, with a moving involute	The 1st caustic is the locus of 2nd foci of osculating Kepler conics
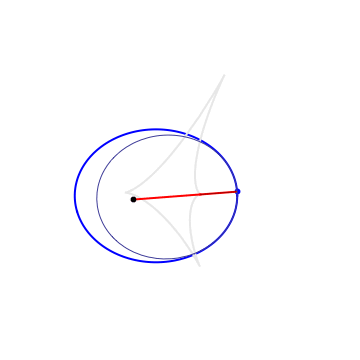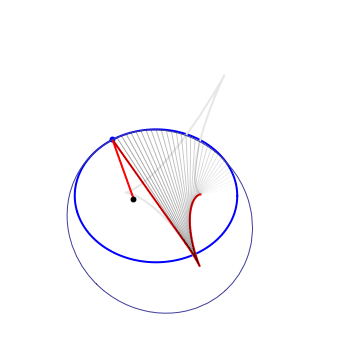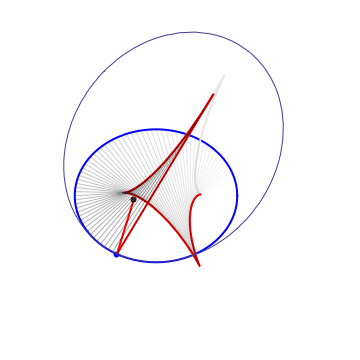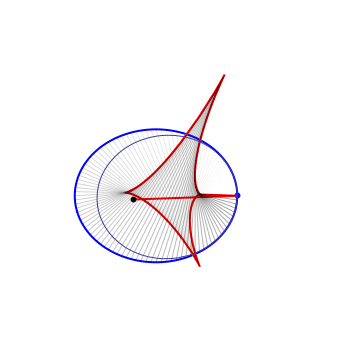
2nd foci of osculating ellipses+hyperbolas	A sring construction, recovering the billiard table from the 1st caustic